Перейти к:
КЛАССИФИКАЦИЯ СОСТОЯНИЯ РАСТЕНИЙ СРЕДСТВАМИ ТЕКСТУРНОГО ВЕЙВЛЕТ-АНАЛИЗА И МАШИННОГО ОБУЧЕНИЯ
https://doi.org/10.35266/1999-7604-2024-1-3
Аннотация
В данной работе предложен метод, комбинирующий вейвлет-преобразования и методы машинного обучения, для классификации состояния растительных культур по цветным цифровым изображениям. Входными данными для классификации являлся сформированный вектор текстурных признаков Харалика. Реализована программа на высокоуровневом языке программирования Python для классификации цифровых изображений с использованием многоуровневого дискретного вейвлет-преобразования Добеши и классификационных методов машинного обучения – классической логистической регрессии и персептрона. Показана эффективность предложенного метода в решении задачи многоклассовой классификации изображений, сделаны соответствующие выводы, оценены перспективы метода.
Ключевые слова
Для цитирования:
Брыкин В.В., Брагинский М.Я., Тараканов Д.В., Тараканова И.О. КЛАССИФИКАЦИЯ СОСТОЯНИЯ РАСТЕНИЙ СРЕДСТВАМИ ТЕКСТУРНОГО ВЕЙВЛЕТ-АНАЛИЗА И МАШИННОГО ОБУЧЕНИЯ. Вестник кибернетики. 2024;23(1):23-30. https://doi.org/10.35266/1999-7604-2024-1-3
For citation:
Brykin V.V., Braginsky M.Ya., Tarakanov D.V., Tarakanova I.O. CLASSIFICATION OF PLANTS HEALTH VIA TEXTURE WAVELET ANALYSIS AND MACHINE LEARNING. Proceedings in Cybernetics. 2024;23(1):23-30. (In Russ.) https://doi.org/10.35266/1999-7604-2024-1-3
ВВЕДЕНИЕ
Сегодня цифровизация сельского хозяйства, где полевые условия контролируются с помощью автономных систем, набирает все большие обороты. При создании систем подобного рода необходимо решать задачи идентификации болезни растений, анализировать динамику их роста.
Выявление болезней растений на ранней стадии и их своевременное предотвращение позволяет избежать больших потерь с точки зрения качества, количества и финансов. Таким образом, для укрепления экономики и сельского хозяйства государство нуждается в системах, способных выявлять болезни растений с высокой точностью и скоростью.
Имеется большая потребность в новых технологиях, отслеживающих рост растений и прогнозирующих воздействие на него различных факторов. В большинстве случаев болезни можно проследить по состоянию побегов растения (стебля, листьев). Значит, идентификация растений, выявление болезней, анализ роста играют существенную роль в успешном выращивании агрономических культур.
Все операции, связанные с обработкой изображений, выполняются в цветовом пространстве RGB, являющемся одним из основных способов представления изображений.
МАТЕРИАЛЫ И МЕТОДЫ
Вейвлет-преобразование
Вейвлет-преобразование представляет собой многомасштабное и многоразрешающее преобразование, позволяющее извлекать из изображения высокочастотные и низкочастотные компоненты. В данной работе используется дискретное двумерное вейвлет-преобразование Добеши (DWT2, вейвлет ‘db2’). Это означает, что квадратное изображение будет передано в качестве входных данных для вейвлет-функции, которая разделит все изображение на 4 компоненты (рис. 1).
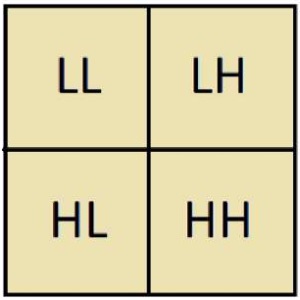
Рис. 1. Принцип одноуровневого двумерного вейвлет-разложения исходного изображения
Примечание: составлено по [1].
Компоненты на рис. 1 – квадранты поддиапазонов частот, где L – низкая частота, H – высокая частота. Разложение может быть многоуровневым, где n – число уровней разложения. LL-квадрант представляет собой аппроксимацию исходного изображения (cAn), HL – его вертикальные детали (cVn), LH – горизонтальные детали (cHn), HH – диагональные составляющие (сDn) [1–4].
Текстура наряду с цветом является самой важной особенностью, если необходимо обнаружить какой-либо объект. Это относится и к классификации состояния растений – любое заболевание отличается характерным распространением по организму и цветом. На основе расположения пикселей на изображении появляется возможность идентифицировать любой объект.
Существует множество способов текстурного анализа. Здесь используется метод текстурных признаков Харалика. Эти признаки рассчитываются на основе матрицы совпадения уровней серого (gray-level co-occurrence matrix, GLCM), являющейся оценкой плотности распределения вероятностей второго порядка p2 (P, Q, Z, Y), полученной по одному изображению в предположении, что плотность вероятности p2 зависит лишь от взаимного расположения P и Q. При этом Z является числом, обозначающим учет соседних пикселей, в том числе их расстояния от пикселя интереса. Y – значение ориентации пикселя интереса и соседних пикселей (в градусах) в интервале [0; 2π) с шагом π/4.
Проще говоря, GLCM-матрица строится на основе вычислений частоты встречаемости пикселя с интенсивностью i с пикселем интенсивности j. Каждый элемент (i, j) в матрице смежности описывает число случаев, когда пиксель со значением i встречается с пикселем со значением j [5].
Хотя GLCM-матрица и представляет собой текстурные свойства, но она неудобна при непосредственном анализе изображения. Признаки Харалика, вычисляемые на ее основе, зарекомендовали себя куда лучше. В данной работе использовались 4 информативных признака, дающих наибольшую итоговую точность, из 14 возможных:
- Контраст. Измеряет пространственную частоту изображения:
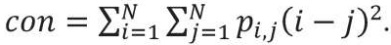 (1)
(1)
- Несходство. Мера расстояния между парами пикселей в интересующей области:
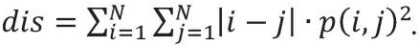 (2)
(2)
- Энергия (второй угловой момент). Измеряет текстурную однородность изображения:
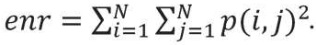 (3)
(3)
- Однородность (обратный разностный момент). Измеряет однородность изображения, которая возрастает при уменьшении тона серого:
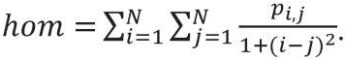 (4)
(4)
Алгоритм классификации
Целью данной работы является классификация большого числа цифровых изображений растений на основе информации об их текстуре и цвете. Алгоритм классификации основан на совместном применении текстурных признаков Харалика, вейвлет-преобразования Добеши и многослойной нейронной сети.
Общий порядок действий алгоритма представлен в схеме на рис. 2.
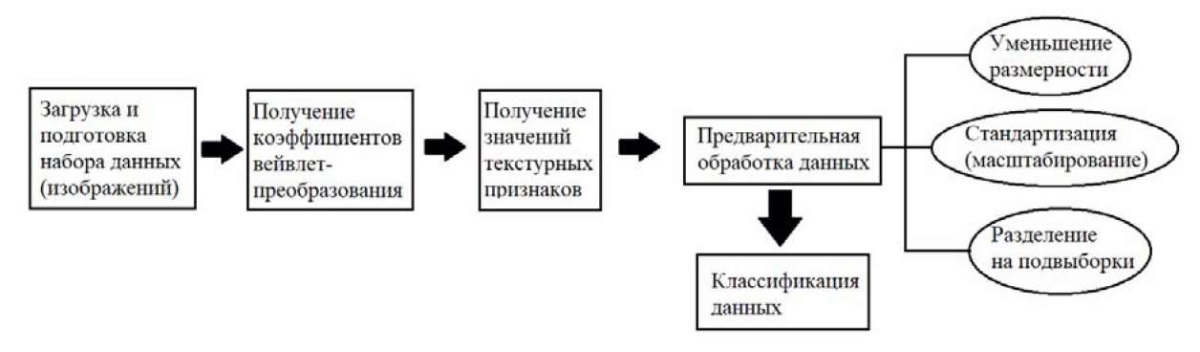
Рис. 2. Схема предлагаемого алгоритма классификации
Примечание: составлено авторами.
Как можно увидеть из рис. 2, после инициализации набора данных и его предварительной обработки к каждому изображению применяется дискретное двумерное вейвлет-преобразование Добеши. Полученные коэффициенты затем группируются по квадрантам поддиапазонов частот, помогая извлекать текстурные признаки, которые передаются в качестве входных данных для классификационных методов.
Загрузка и подготовка данных
Исходные данные приведены на рис. 3 и представляют собой набор цветных цифровых изображений, распределенных по директориям, имена которых соответствуют названиям классов. Изображения были предварительно подготовлены – приведены к единому размеру 256×256 пикселей и распределены поровну на каждый класс (сбалансированы по 2 200 единиц в каждом классе, суммарно 17 600 фотографий). Таким образом, количество директорий совпадает с числом классов, т. е. 8.

Рис. 3. Классы исходных данных
Примечание: составлено авторами.
Датасет на рис. 3 был загружен с общедоступного ресурса по исследованию данных Kaggle.
Получение значений признаков
Результат вейвлет-преобразования, описанного выше, приведен на рис. 4 на примере исходных данных.
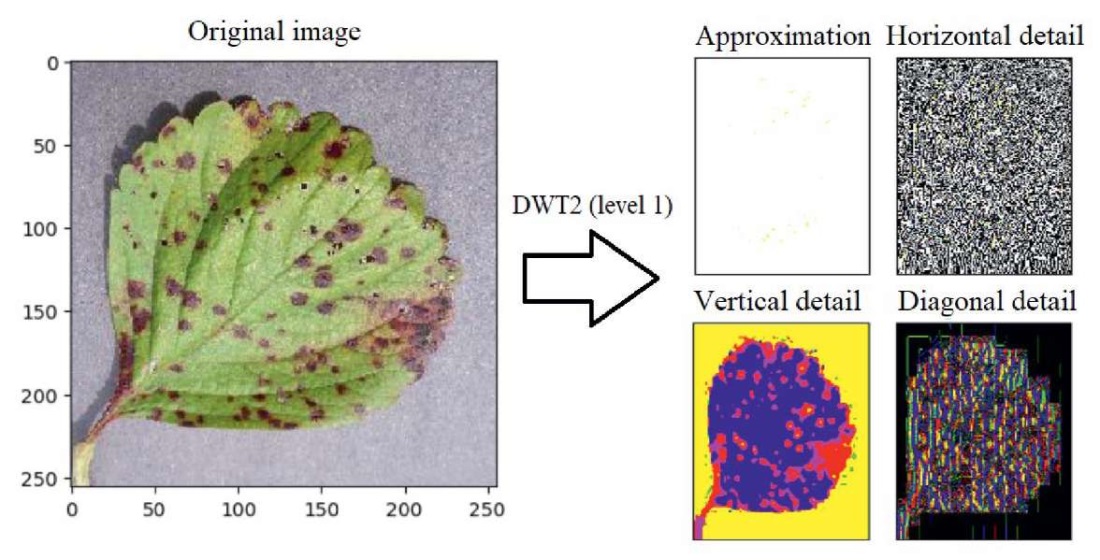
Рис. 4. Пример одноуровневого двумерного вейвлет-разложения исходного изображения
Примечание: составлено авторами.
Так как каждый из 4-х квадрантов представляет собой RGB-область размером 128×128 пикселей исходного изображения, для каждого из 3-х его каналов (красная, зеленая и синяя компонента) строится симметричная нормированная GLCM-матрица в 256 оттенках серого. Значит, для целого изображения будет вычислено 12 GLCM-матриц оттенков серого. В свою очередь, каждая такая матрица порождает 4 значения признаков Харалика, описанных ранее. Таким образом, при одноуровневом вейвлет-преобразовании одно цветное изображение будет описано вектором-строкой из 48 коэффициентов-признаков Харалика. Вообще длина вектора может быть рассчитана по следующей формуле:
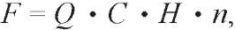 (5)
(5)
где Q = 4 – количество областей (квадрантов), на которые разбивается изображение;
C = 3 – количество каналов цветного изображения (в данном случае RGB);
H – количество признаков Харалика, порождаемых GLCM-матрицей (здесь H = 4);
n – число уровней вейвлет-преобразования.
Формула (5) представляет расчет итогового числа текстурных признаков на единицу исходных данных.
Логично, что с увеличением количества n уровней вейвлет-разложения будет пропорционально расти и размерность F вектора признаков. В текущей работе число уровней разложения n было определено эмпирически. Для восьми классов оптимально значение n = 3. Отсюда итоговое число признаков F = = 4 • 3 • 4 • 3 = 144. Для удобства восприятия и дальнейших расчетов все коэффициенты – это массив размером m × k (где m = 17 600 – общее число изображений в наборе данных, k = F + 1 = 145 – итоговое количество признаков Харалика и метка класса, закодированная способом «label encoding») – были записаны в CSV-файл средствами библиотеки Pandas языка Python (рис. 5).
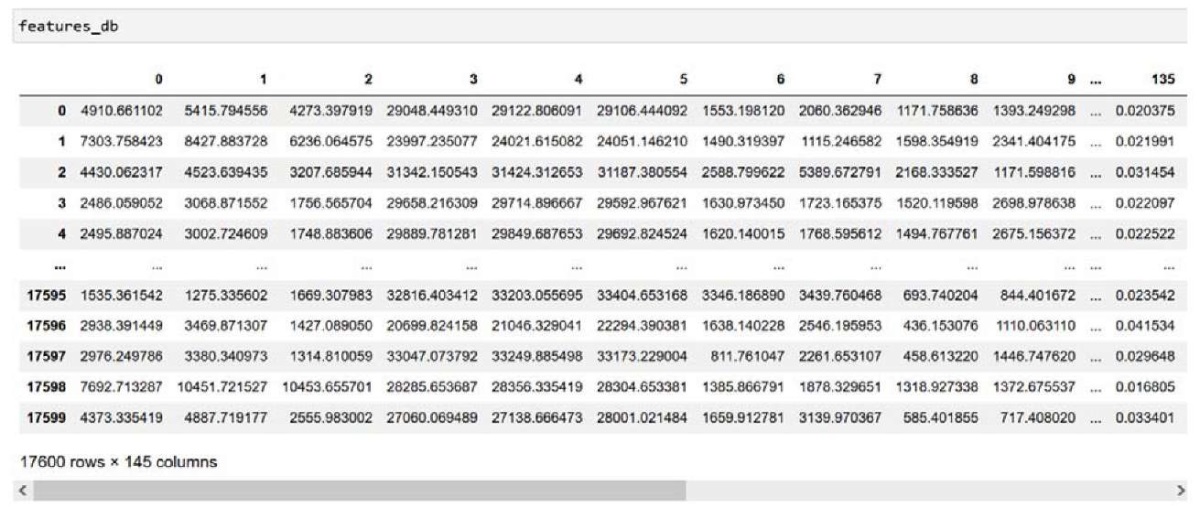
Рис. 5. Текстурные признаки Харалика для исходного датасета
Примечание: составлено авторами.
Стоит также упомянуть другие модули и библиотеки Python, задействованные в данной работе:
Os – для работы с операционной и файловой системами (загрузка и инициализация набора данных);
OpenCV – для анализа изображений;
NumPy – для работы с многомерными массивами;
Matplotlib – для визуализации данных и вычислений;
PyWt – для вейвлет-вычислений;
Scikit-learn – для операций машинного обучения.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Фактически датафрейм из рис. 5 представляет собой готовую для дальнейших вычислений и решения основной задачи базу данных признаков изображений. Входными данными для обучения нейронной сети будут являться значения признаков Харалика (все столбцы датафрейма, кроме последнего), выходными – последний столбец датафрейма с закодированными метками классов.
Следующим шагом является предварительная обработка данных.
Во-первых, это разделение на обучающую и тестовую выборки в оптимальном соотношении 70 к 30.
Во-вторых, стандартизация: некоторые характеристики имеют широкий диапазон значений и в процессе классификации могут создать систематическую ошибку. Вспомогательный класс StandartScaler масштабирует данные так, чтобы они имели нулевое среднее значение и единичную дисперсию (μ = 0, σ = 1). Важно то, что здесь выполняется стандартизация лишь входных данных, поскольку выходные содержат только закодированные метки [6][7].
В-третьих, уменьшение размерности, являющееся самым важным шагом предобработки. Оно улучшает скорость работы методов машинного обучения, снижает требования к памяти при минимальных информационных потерях. Одним из распространенных методов уменьшения размерности данных является метод главных компонент (principal component analysis, PCA). В библиотеку Scikit-learn этот метод уже встроен, поэтому главной задачей становится правильный выбор количества главных компонент набора данных. Чтобы ее решить, нужно построить график зависимости параметра «Variance explained» от количества главных компонент (рис. 6).
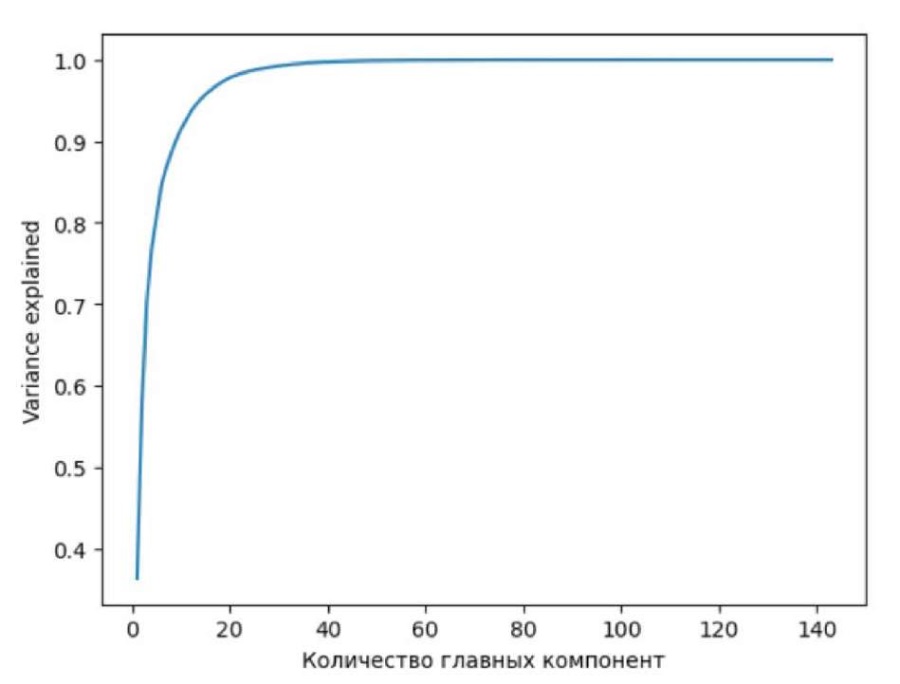
Рис. 6. График зависимости параметра «Variance explained»
от числа главных компонент
Примечание: составлено авторами.
Параметр «Variance explained» характеризует степень потери полезной информации о данных. Чем ближе он к 1, тем больше информации сохраняется для анализа [8].
Как можно заметить из рис. 6, уже при числе N = 40 компонент значение вариативности практически достигает единицы, так что именно этот показатель будет взят для дальнейших расчетов. Таким образом, с минимальными потерями удалось снизить размерность данных более чем в три раза (со 144 до 40 признаков).
Непосредственно классификация выполнялась двумя способами:
- классическим алгоритмом машинного обучения – логистической регрессией;
- базовой моделью искусственной нейронной сети – персептроном.
Результаты приведены в сравнительной таблице.
Таблица
Результаты нейросетевой классификации
Метод классификации | Метрика | |||
accuracy | precision | recall | f-score | |
Логистическая регрессия | 88 % | 0.88 | 0.87 | 0.87 |
Персептрон | 84 % | 0.84 | 0.83 | 0.84 |
Примечание: составлено авторами.
Как можно видеть из таблицы, благодаря комбинированию методов текстурного анализа и машинного обучения удалось достичь высоких показателей точности – до 88 %.
ЗАКЛЮЧЕНИЕ
В статье предложен алгоритм многоклассовой классификации состояния растений с использованием текстуры изображений, отличающийся совокупным применением методов вейвлет-анализа и машинного обучения, что позволило достичь хороших результатов (до 88 % точности).
Перспективы совершенствования предложенного метода могут включать выбор наиболее оптимального типа вейвлет-преобразования и классификационного метода машинного обучения.
Список литературы
1. Vyas A., Paik J. Review of the application of wavelet theory to image processing. IEIE Transactions on Smart Processing & Computing. 2016;5(6):403‒417.
2. Балаганский А. Ю., Гребеньков А. А. Вейвлет-преобразование для обработки изображений системы управления отоплением с применением методов машинного обучения // Информация и образование: границы коммуникаций. 2022. № 14. С. 147–150.
3. Мельникова Ю. С. Анализ и обработка медицинских изображений с помощью метода вейвлетана лиза в ветеринарии // Фундаментальные и прикладные исследования в информатике и цифровизации : материалы симпозиума XVIII (L) Междунар. науч. конф. студентов, аспирантов и молодых ученых, приуроченной к 50-летию КемГУ, 26 апреля 2023 г., г. Кемерово. Кемерово : Кемеровский государственный университет, 2023. С. 138–141.
4. Alekseev V. V., Kaliakin I. V. The role of sampling rate in wavelet transform decomposition. In: Proceedings of the XIX IEEE International Conference on Soft Computing and Measurements SCM 2016, May 25‒27, 2016, Saint Petersburg. St. Petersburg; 2016. p. 392–394.
5. Ковалева И. Л. Текстурные признаки изображений. Минск : Белорусский национальный технический университет, 2010. 26 с.
6. Предварительная обработка данных. URL: https://scikit-learn.ru/6-3-preprocessing-data/ (дата обращения: 25.12.2023).
7. Как писать преобразователи данных в Sklearn. URL: https://habr.com/ru/companies/skillfactory/articles/675876/ (дата обращения: 25.12.2023).
8. Kumar A. PCA Explained Variance Concepts with Python Example. 2023. URL: https://vitalfl ux.com/pca-explained-variance-concept-python-example/ (дата обращения: 27.12.2023).
Об авторах
В. В. БрыкинРоссия
аспирант
М. Я. Брагинский
Россия
кандидат технических наук, доцент
Д. В. Тараканов
Россия
кандидат технических наук, доцент
И. О. Тараканова
Россия
аспирант, ассистент
Рецензия
Для цитирования:
Брыкин В.В., Брагинский М.Я., Тараканов Д.В., Тараканова И.О. КЛАССИФИКАЦИЯ СОСТОЯНИЯ РАСТЕНИЙ СРЕДСТВАМИ ТЕКСТУРНОГО ВЕЙВЛЕТ-АНАЛИЗА И МАШИННОГО ОБУЧЕНИЯ. Вестник кибернетики. 2024;23(1):23-30. https://doi.org/10.35266/1999-7604-2024-1-3
For citation:
Brykin V.V., Braginsky M.Ya., Tarakanov D.V., Tarakanova I.O. CLASSIFICATION OF PLANTS HEALTH VIA TEXTURE WAVELET ANALYSIS AND MACHINE LEARNING. Proceedings in Cybernetics. 2024;23(1):23-30. (In Russ.) https://doi.org/10.35266/1999-7604-2024-1-3















