Перейти к:
ОБРАБОТКА АКУСТИЧЕСКИХ СИГНАЛОВ ПРИ НЕСАНКЦИОНИРОВАННОМ ВОЗДЕЙСТВИИ НА МАГИСТРАЛЬНЫЙ ТРУБОПРОВОД
https://doi.org/10.35266/1999-7604-2024-1-8
Аннотация
В статье представлен способ обработки акустических сигналов при возникновении несанкционированного действия на магистральном трубопроводе на примере проведенных экспериментов по имитации незаконной врезки в виде сверления тела металлической трубы. В рамках эксперимента были записаны акустические сигналы и проведена обработка на основе метода быстрого преобразования Фурье. По результатам были идентифицированы пики характерных частот в пределах каждого эксперимента. Исследование направлено на повышение безопасности протяженных объектов особой государственной важности путем определения угрозы по характерным пикам частот получаемых при обработке акустических сигналов от противоправных действий и, как следствие, оперативного оповещения службы безопасности.
Ключевые слова
Для цитирования:
Романовский М.В., Солдатов А.И. ОБРАБОТКА АКУСТИЧЕСКИХ СИГНАЛОВ ПРИ НЕСАНКЦИОНИРОВАННОМ ВОЗДЕЙСТВИИ НА МАГИСТРАЛЬНЫЙ ТРУБОПРОВОД. Вестник кибернетики. 2024;23(1):60-67. https://doi.org/10.35266/1999-7604-2024-1-8
For citation:
Romanovsky M.V., Soldatov A.I. ACOUSTIC SIGNALS PROCESSING IN UNAUTHORIZED OPERATION ON THE MAIN PIPELINE. Proceedings in Cybernetics. 2024;23(1):60-67. (In Russ.) https://doi.org/10.35266/1999-7604-2024-1-8
ВВЕДЕНИЕ
Магистральный трубопроводный транспорт относится к объектам особой стратегической государственной важности согласно [1], которые следует соответственно охранять, применяя новейшие методы физической защиты (ФЗ).
По состоянию на 2022 г., согласно Федеральной службе государственной статистики [2], протяженность магистральных трубопроводов, перекачивающих нефть и газ в России, составляет 256 тыс. километров, при этом общий объем грузооборота продуктов за тот же год в среднем составил 2 653 млрд т∙км. Охрана настолько протяженных объектов является нетривиальной задачей и требует компромиссного подхода. Ввиду важности такого объекта необходимо организовать должную защиту в соответствии с общими принципами построения системы физической защиты (СФЗ): своевременность, зональность, равнопрочность, адекватность и другие общетехнические принципы. С одной стороны, необходимо организовать такую СФЗ, которая бы своевременно оповещала персонал службы безопасности, сотрудники безопасности контролировали объект и сам объект был бы равно защищен по всей протяженности, но, с другой стороны, нерационально охранять объект в сложных климатических регионах, например Арктической зоне, ввиду больших экономических затрат.
По этой причине в основном применяют технические средства (ТС) обнаружения несанкционированных действий и инженерные средства (ИС), позволяющие защитить объект, например, забором, колючей проволокой, или расположить трубопровод под землей и наделить его свойствами самозащищенности.
Тем не менее это не всегда помогает. Так, по статистике, приведенной в официальном отчете ПАО «Транснефть» [3], число незаконных врезок в 2019 г. составило 219 шт. При этом наносится не только экономический урон, который оценивается примерно в 37 млрд руб. в год, но и экологический. Так, последний инцидент, случившийся на участке Самотлор – Нижневартовск в 2022 г., устранялся 40 специалистами и 15 единицами техники [4]. При этом ответственные за данный инцидент с хищением так и не были установлены.
Метод, описанный в данной работе, позволит не только зарегистрировать событие несанкционированного действия, как это описано в патенте на изобретение [5], но и поможет определить вид угрозы после обработки считанного акустического сигнала и сопоставленного с эталонной базой звуковых сигналов. Кроме того, данный способ понизит вероятность ложного срабатывания ТС обнаружения системы безопасности.
Описанный метод основан на быстром преобразовании Фурье, позволяющем обработать полученный акустический сигнал, переведя его в частотный спектр. Применив его в спектральной обработке, можно получить зависимость плотности сигнала от частоты и выявить характерные частотные пики для того или иного взаимодействия с охраняемым объектом, например сверление, удар и вваривание. Более подробно метод описан в [6] и [7].
Обработка вышеописанным методом в рамках эксперимента проводилась в аналитическом программном обеспечении MATLAB.
МАТЕРИАЛЫ И МЕТОДЫ
Спектральный анализ – это метод, используемый для изучения частотных компонентов сигнала. Одним из наиболее часто используемых методов спектрального анализа является быстрое преобразование Фурье (БПФ). Он основан на теореме о том, что любой периодический сигнал может быть представлен в виде суммы комплексных экспоненциальных функций. Это позволяет разложить сигнал на его частотные составляющие, которые могут быть проанализированы для определения характеристик сигнала.
БПФ работает путем разбиения входного сигнала на перекрывающиеся сегменты и вычисления их Фурье-преобразования. Затем результаты объединяются для получения итогового спектра сигнала. Этот процесс значительно ускоряет вычисление Фурье-преобразования по сравнению с традиционным методом, который требует большого количества времени и вычислительных ресурсов [6].
Одним из основных преимуществ БПФ является его высокая точность и эффективность. Он позволяет получить более точные результаты по сравнению с другими методами спектрального анализа, такими как преобразование Фурье, за меньшее время. Кроме того, БПФ может обрабатывать большие объемы данных без потери точности, что делает его идеальным для анализа сложных сигналов.
Метод БПФ описывается следующими этапами [7].
Разбиение сигнала. На данном этапе сигнал разбивается на перекрывающиеся сегменты, каждый из которых достаточно короткий, чтобы его можно было обработать с помощью быстрого преобразования Фурье. Длина сегмента обычно выбирается кратной степени числа 2, поскольку это позволяет эффективно использовать алгоритм БПФ.
Вычисление Фурье-преобразования. Далее для каждого сегмента вычисляется его Фурье-преобразование, которое представляет собой спектр частот, присутствующих в данном сегменте.
Умножение на весовые коэффициенты. Полученные Фурье-преобразования умножаются на специальные весовые коэффициенты, которые обеспечивают точность результата и минимизируют ошибки.
Сложение преобразований. Фурье-преобразования всех сегментов складываются вместе с учетом их весовых коэффициентов. В результате получается спектр всего исходного сигнала.
Интерполяция и фильтрация. После получения спектра сигнала его можно интерполировать и фильтровать, чтобы получить более точную информацию о частотах и амплитудах различных составляющих сигнала.
Обратное преобразование. Если необходимо восстановить исходный сигнал из его спектра, то выполняется обратное преобразование Фурье полученного спектра. Далее по статье эти этапы применяются в практическом эксперименте в более подробном виде.
Для демонстрации обработки сигнала методом БПФ и применения спектральной обработки воспользуемся программным обеспечением MATLAB и записанным звуковым сигналом удара молотком по металлической трубе.
В результате записи сигнала можно получить сигнал, представленный на рис. 1. Он представляет собой короткий импульс удара с продолжительным затуханием.
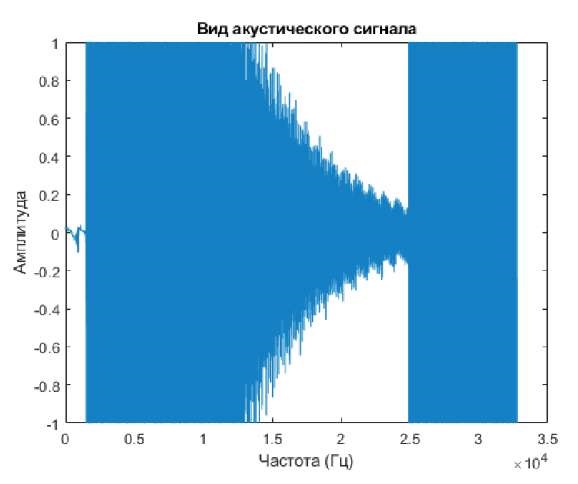
Рис. 1. Визуализация сигнала
Примечание: составлено авторами на основании данных, полученных в исследовании.
После обработки с помощью быстрого преобразования Фурье можно попытаться визуализировать спектр на рис. 2.
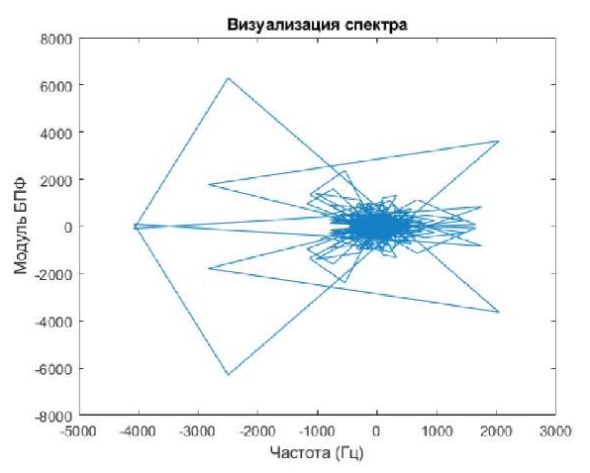
Рис. 2. Визуализация спектра обработанного сигнала с помощью БПФ
Примечание: составлено авторами на основании данных, полученных в исследовании.
Вид такого графика обусловлен тем, что функция plot строит график значений комплексной величины на комплексной плоскости, поэтому необходимо построить амплитудный спектр сигнала, воспользовавшись функцией abs для вычисления модуля комплексного вектора, результат представлен на рис. 3 [8].
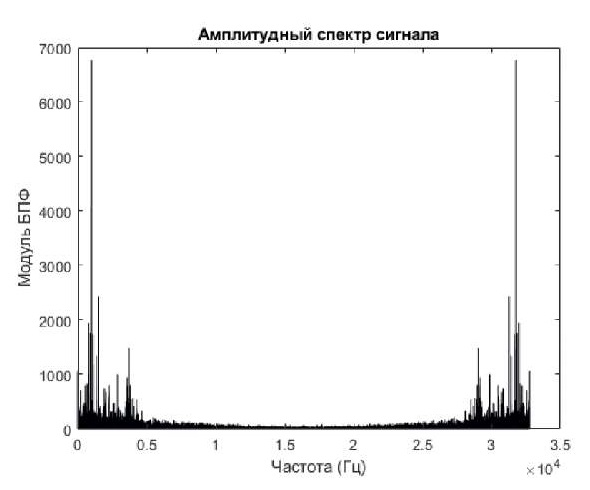
Рис. 3. Амплитудный спектр сигнала
Примечание: составлено авторами на основании данных, полученных в исследовании.
В итоге получается действительный сигнал, при этом выход функции учитывает область положительных и отрицательных частот.
Для представления графика в более привычном виде зеркально относительно нулевой частоты необходимо воспользоваться функцией fftshift с ограничением предела частоты от –2 до 2 кГц. Получившийся амплитудный спектр сигнала представлен на рис. 4.
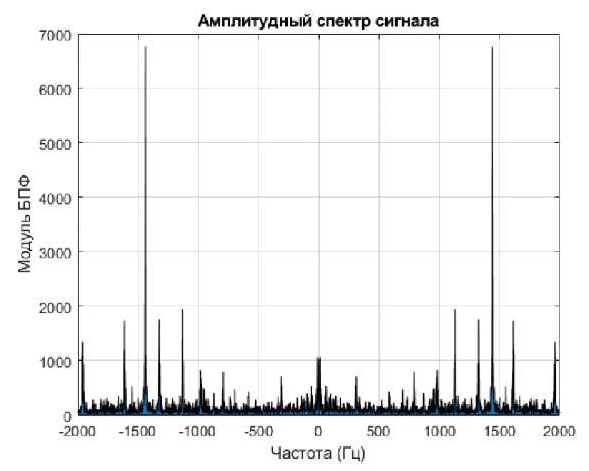
Рис. 4. Амплитудный спектр сигнала, отраженный относительно нуля
Примечание: составлено авторами на основании данных, полученных в исследовании.
Так как спектр симметричен, достаточно рассматривать только область положительных частот. Результат приведен на рис. 5, как видно, здесь присутствует гармоническая структура спектра.
При получении результата, представленного на рис. 6, для нахождения максимумов использовалась функция findpeaks. Данная функция используется для нахождения положительных или отрицательных пиков входных данных или сигнала и позволяет определить такие параметры, как местоположение пиков, их ширина и т. д. Функция findpeaks в MATLAB используется для нахождения пиков (локальных максимумов) во временном ряде или массиве данных. Она принимает в качестве аргумента массив данных и возвращает индексы локальных максимумов в этом массиве. Локальный максимум – это точка данных, которая больше значений соседних точек с обеих сторон и в результате возвращает координаты этих точек (индексы элементов массива) [8].
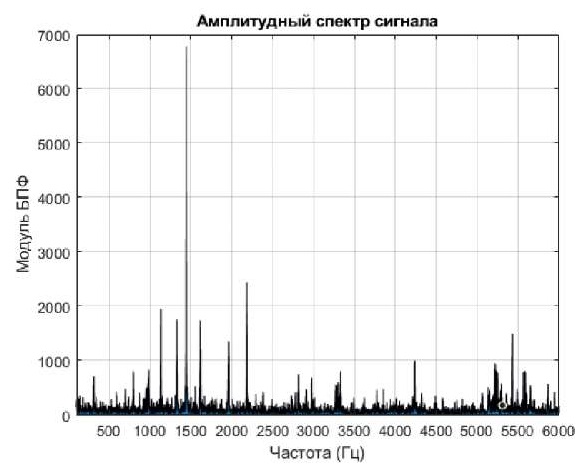
Рис. 5. Амплитудный спектр сигнала области положительных частот
Примечание: составлено авторами на основании данных, полученных в исследовании.
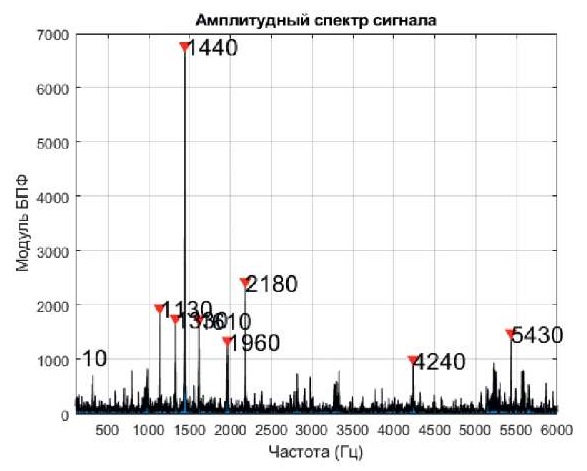
Рис. 6. Амплитудный спектр сигнала области положительных частот
с определением амплитудных максимумов
Примечание: составлено авторами на основании данных, полученных в исследовании.
В данной работе использовался синтаксис [peaks, locations] = findpeaks (data), в таком виде функция возвращает дополнительно индексы, при которых происходят пики, где peaks – вектор значений максимумов, а locations – вектор индексов элементов массива data, на которых расположены найденные максимумы. Итоговый запрос для анализа данных выглядит как [~, locs] = findpeaks (pxx,’MinPeakHeight’,0.005,’MinPeakDistance’, nFFT/500), где pxx – это спектральная плотность мощности сигнала, а nFFT – длина сигнала БПФ [8].
При этом происходит округление значения частот и явно выявляется доминирующая частота 1449 Гц.
Чтобы убедиться, что расчеты, проведенные в MATLAB, верны, необходимо провести обратное преобразование Фурье по измененным данным с помощью функции ifft.
Так как для эксперимента бралось достаточно большое количество точек для представлений, то в частотной области особых искажений сигнала после преобразования нет. Также это можно продемонстрировать на временном спектре амплитуд до и после эксперимента, изображенном на рис. 7 а–б соответственно.
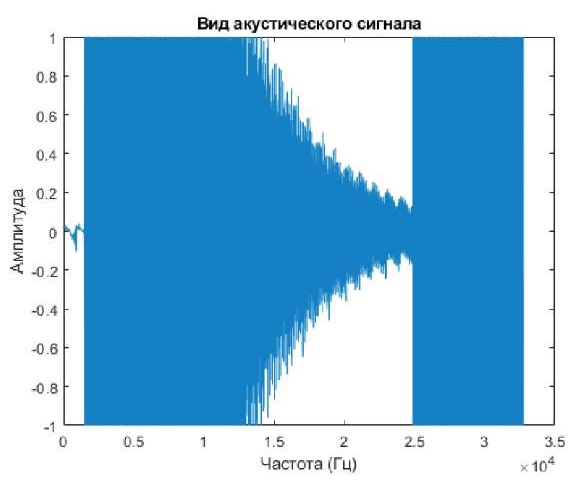
Рис. 7а. Сигнал до БПФ
Примечание: составлено авторами на основании данных, полученных в исследовании.
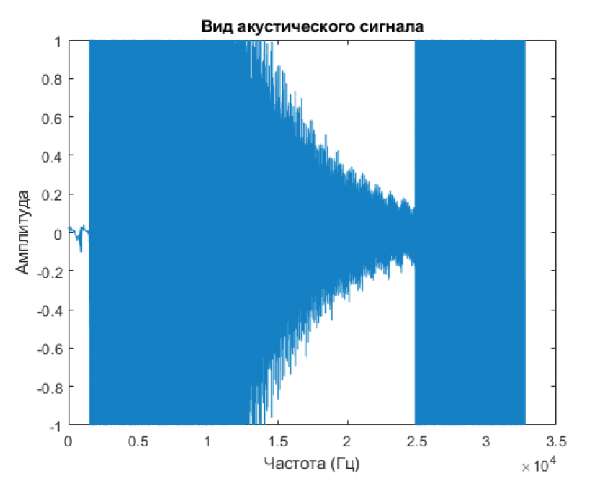
Рис. 7б. Сигнал после ОБПФ
Примечание: составлено авторами на основании данных, полученных в исследовании.
На основе вышеописанного опыта можно убедиться, что с помощью БПФ можно выделить характерные частоты для определенного сигнала. Такой метод хорош для обработки единичного сигнала, для проведения анализа частот в основном используют метод спектральной обработки сигнала.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Далее необходимо провести спектральный анализ, основываясь на методе БПФ.
Одна из особенностей спектральной обработки с помощью БПФ – это векторный вход алгоритма БПФ. Алгоритм всегда работает с массивами значений входного сигнала, и на выходе получается вектор комплексных отчетов спектра сигнала [8]. Алгоритм требует векторного входа, но отсчеты сигнала зачастую поступают скалярно, то есть по одному. Поэтому перед непосредственным БПФ осуществляется буферизация, или накопление, отчетов в вектор.
В алгоритме БПФ важную роль играют окно и отсчеты, которые влияют на точность и качество спектральной обработки сигнала [9], где окном является входной вектор временных отсчетов, а отсчеты БПФ – это выходные временные отсчеты.
Для дискретного сигнала x [n] формула для вычисления периодограммы выглядит следующим образом [10]:
P (f) = (|X (f)| 2)/N,
где P (f) – СПМ для частоты f,
X (f) – комплексный спектр сигнала после применения БПФ,
|X (f)| 2 – квадрат модуля комплексного спектра (амплитуда мощности),
N – общее количество отсчетов в сигнале.
Эта формула представляет основной подход к вычислению СПМ. Однако существуют и другие методы, такие как периодограмма с использованием оконных функций, методы сглаживания и интерполяции для улучшения точности и качества СПМ [10].
Спектральный анализ также выполнялся в программном обеспечении MATLAB. Входными данными является также периодический удар металлическим предметом по металлической конструкции в виде отрезка трубы, представленный на рис. 1.
В этом опыте воспользуемся функцией pwelch для оценки спектральной плотности мощности сигнала.
Входными параметрами являются: количества отсчетов входного вектора, длины БПФ, отсчетов перекрытия спектра, типа оконной функции и тип оконной функции, которая представлена на рис. 8. Входные параметры указаны в таблице.
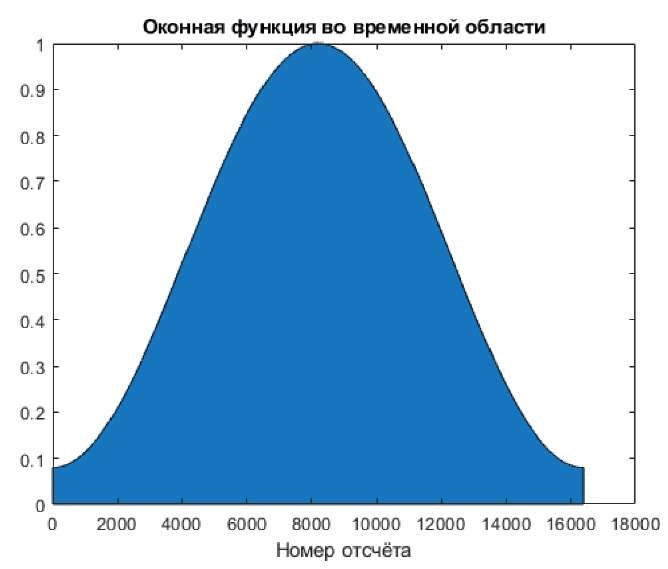
Рис. 8. Оконная функция во временной области
Примечание: составлено авторами на основании данных, полученных в исследовании.
Таблица
Входные параметры
Параметр | Значение |
Длина входного вектора (входного окна) | 2 ¹² |
Длина БПФ (Nfft) | 2 ¹⁴ |
Количество отсчетов перекрытия | 0 |
Тип оконной функции | Окно Хемминга |
Примечание: составлено авторами.
После запуска основной функции pwelch получается график, представленный на рис. 9.
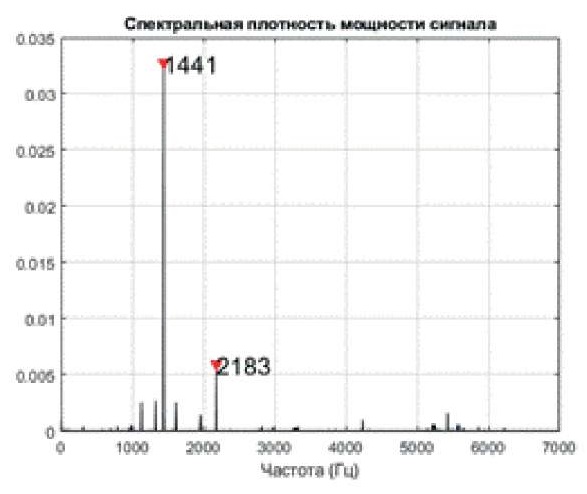
Рис. 9. Спектральная плотность мощности сигнала
Примечание: составлено авторами на основании данных, полученных в исследовании.
Разрешение рассчиталось в районе 2,92 Гц, значения положения пиков рассматриваются с точностью до 3 Гц, так как округляется функцией round.
При этом при увеличении окна переменной nwindow можно добиться подъема пиков и рассмотрения гармоник более детально, энергетики которых не хватало в коротком отрезке входного сигнала. А при увеличении количества точек БПФ переменной nFFT частотная сетка станет более плотной и положение пиков будет оцениваться более точно.
ЗАКЛЮЧЕНИЕ
Таким образом, с помощью функции pwelch получилось добиться детального спектрального анализа, и при сравнении двух экспериментов с обычным переводом в частотный спектр акустического сигнала и полноценного спектрального анализа можно прийти к выводу, что спектральная плотность мощности сигнала дает нам большую детализацию и больше информации о сигнале, чем обычный метод обработки быстрым преобразованием Фурье.
Далее планируется провести серию экспериментов с разным оборудованием и применением шумоподавления и сравнить полученные результаты для калибровки и, как следствие, более точной записи акустического сигнала в заданных условиях эксперимента.
Список литературы
1. О магистральном трубопроводном транспорте : проект федер. закона Российской Федерации № 99045329-2. URL: https://docs.cntd.ru/document/902358183 (дата обращения: 19.01.2024).
2. Транспорт в России : стат. сб. М. : Росстат, 2022. 101 с.
3. Ущерб «Транснефти» от криминальных врезок в 2020 г. превысил 600 млн руб // Транснефть : официальный сайт. URL: https://www.transneft.ru/media-center/newspress/publications/ushcherbtransnefti-ot-kriminalnykh-vrezok-v-2020-g-prevysil-600-mln-rub/ (дата обращения: 19.01.2024).
4. АО «Транснефть – Сибирь» ликвидирует последствия криминальной врезки на магистральном нефтепроводе в ХМАО-Югре // Транснефть : официальный сайт. URL: https://siberia.transneft.ru/media-center/newspress/news/ao-transneft-sibir-likvidiruet-posledstviya-kriminalnoy-vrezki-na-magistralnom-nefteprovode-v-khmao-/ (дата обращения: 19.01.2024).
5. Ахмеджанов Р. А., Федотов А. А. Способ обнаружения несанкционированных воздействий на трубопровод : патент 2676386С1 Рос. Федерация. № 2018102654 ; заявл. 23.01.2018 ; опубл. 28.12.2018. URL: https://yandex.ru/patents/doc/RU 2676386C1_20181228?ysclid=lsljscvzgq22421326 (дата обращения: 19.01.2024).
6. Романовский М. В., Солдатов А. И. Спектральная обработка акустических сигналов в системах физической защиты магистральных трубопроводов // Успехи кибернетики. 2023. Т. 4, № 1. С. 72–78. DOI 10.51790/2712-9942-2023-4-1-10.
7. Романовский М. В., Солдатов А. И. Исследование акустических сигналов несанкционированных действий на магистральных нефтегазотрубопроводах // Научные исследования: итоги и перспективы. 2023. Т. 4, № 4. С. 3–8. DOI 10.21822/2713-220X-2023-4-4-3-8.
8. MATLAB и быстрое преобразование Фурье. URL: https://hub.exponenta.ru/post/matlab-i-bystroe-preobrazovanie-fure356 (дата обращения: 19.01.2024).
9. Шамсиев Э. Х., Павлов А. Д. Методы голосовой идентификации человека // Профессиональные коммуникации в научной среде – фактор обеспечения качества исследований : сб. материалов XI Всерос. науч.-практич. конф., 16–17 марта 2022 г., г. Альметьевск. СПб. : ООО «Скифия-принт», 2022. С. 138–142.
10. Кандидов В. П., Чесноков С. С., Шленов С. А. Дискретное преобразование Фурье. М. : МГУ, 2019. 88 с.
Об авторах
М. В. РомановскийРоссия
аспирант
А. И. Солдатов
Россия
доктор технических наук, профессор
Рецензия
Для цитирования:
Романовский М.В., Солдатов А.И. ОБРАБОТКА АКУСТИЧЕСКИХ СИГНАЛОВ ПРИ НЕСАНКЦИОНИРОВАННОМ ВОЗДЕЙСТВИИ НА МАГИСТРАЛЬНЫЙ ТРУБОПРОВОД. Вестник кибернетики. 2024;23(1):60-67. https://doi.org/10.35266/1999-7604-2024-1-8
For citation:
Romanovsky M.V., Soldatov A.I. ACOUSTIC SIGNALS PROCESSING IN UNAUTHORIZED OPERATION ON THE MAIN PIPELINE. Proceedings in Cybernetics. 2024;23(1):60-67. (In Russ.) https://doi.org/10.35266/1999-7604-2024-1-8














