Перейти к:
Разработка архитектуры нейросетевого декодирования, основанной на системах стробирования и распределения весовых коэффициентов
https://doi.org/10.35266/1999-7604-2024-3-6
Аннотация
Проведен анализ рабочей архитектуры для алгоритма нейросетевого декодирования, основанного на распространении доверия, в которой контролируется количество обучаемых параметров и вычислений в нейронной сети благодаря распределению весов и эффективному вычислительному графу. Операция распределения весовых коэффициентов включает в себя вычисление взвешенной суммы выходных сигналов нейронов уровня слоя, умноженной на соответствующие веса, и сложение смещений. Метод выделения участка данных предполагает применение нелинейной функции активации к выходным сигналам нейронов. После нескольких итераций локального декодирования значение потерь рассчитывается с использованием функции потерь среднеквадратичной ошибки. Результаты моделирования показывали, что производительность улучшается по сравнению со стандартным декодером, построенного с использованием стандартного алгоритма распространения доверия (belief propagation, BP), благодаря применению подхода, подобного нейросетевому алгоритму BP. Предложена надежная схема декодирования на основе нейронной сети, предназначенная для систем беспроводной связи. Данная архитектура рекуррентной нейронной сети, основанная на алгоритмах стробирования и распределения весовых коэффициентов, предназначена для выполнения декодирования распространения доверия без предварительного знания схемы кодирования.
Ключевые слова
Для цитирования:
Пирогов А.А., Хорошайлова М.В., Сёмка Э.В. Разработка архитектуры нейросетевого декодирования, основанной на системах стробирования и распределения весовых коэффициентов. Вестник кибернетики. 2024;23(3):46-55. https://doi.org/10.35266/1999-7604-2024-3-6
For citation:
Pirogov A.A., Khoroshailova M.V., Syomka E.V. Development of a neural network decoding architecture based on gating and weight distribution systems. Proceedings in Cybernetics. 2024;23(3):46-55. (In Russ.) https://doi.org/10.35266/1999-7604-2024-3-6
ВВЕДЕНИЕ
Современная система связи должна быть оперативна, достоверна, помехоустойчива, надежна и скрытна. Опираясь на данные требования к связи, можно утверждать, что помехоустойчивое кодирование является неотъемлемой частью цифровой обработки информационных данных. Рассмотрены архитектура каскадного кодека для программируемой логической интегральной схемы (ПЛИС) с использованием внутреннего низкоплотностного кода стандарта DVB-S2 и внешнего кода Рида – Соломона [1], архитектура ПЛИС для квазициклических кодов четности с низкой плотностью (QC-LDPC), основанных на построении идентичной матрицы circulant-1 [2]. Алгоритм декодирования с использованием метода низкой плотности проверки на четность (LDPC) на основе ПЛИС для реализации полностью параллельных LDPC-декодеров предназначен для оптимизации использования логики ПЛИС и уменьшения времени задержки декодирования [3]. Каскадная сетевая структура для распознавания LDPC кодирования вслепую рассматривалась авторами в работе [4]. Декодирование LDPC-алгоритма побитовым адаптивным порогом инверсии бита (adaptive threshold bit flipping, ATBF) исследовали авторы в работе [5].
Коды с исправлением ошибок, имеющие широкое применение при передаче данных, хранении данных и отказоустойчивых вычислениях, предназначены для защиты информации от случайных ошибок. Основным классом помехоустойчивых кодов является класс линейных блочных кодов (LBC). В LBC к строке информационных символов добавляются некоторые дополнительные символы, предназначенные для формирования кодового слова, таким образом, чтобы отделить каждый информационный вектор дальше друг от друга в пространстве кодовых слов. Следовательно, когда на кодовое слово влияет некоторый шум во время передачи или обработки, декодер может исправить ошибку, связав зашумленную строку с ближайшим допустимым кодовым словом.
Современные инструменты машинного обучения, универсальные и простые в использовании могут значительно улучшить производительность декодирования [6]. Нейронные декодеры распространения доверия были представлены как способ улучшения производительности декодирования итерационного алгоритма распространения доверия для линейных блочных кодов короткой и средней длины. Основная идея, которая лежит в основе этих декодеров, заключается в представлении распространения убеждений в виде нейронной сети, позволяющей адаптивно взвешивать процесс декодирования.
Цель: разработка упорядоченной архитектуры, обеспечивающей применение алгоритма нейросетевого распространения доверия для декодирования линейных блочных кодов с улучшенной гибкостью декодера благодаря его возможностям обучения и повышения производительности по сравнению со стандартным декодером BP.
МАТЕРИАЛЫ И МЕТОДЫ
Коды проверки четности низкой плотности (LDPC) были выбраны в стандарте 5G наряду с полярными кодами. Низкоплотностные коды представляют собой класс линейных блочных кодов и являются одними из самых эффективных помехоустойчивых кодов, выполняющими итеративные алгоритмы декодирования. Тем не менее в некоторых случаях использования, таких как IoT (Internet of Things – интернет вещей) с низким энергопотреблением, нельзя применять большие коды из-за сложности их декодирования и их несоответствия относительно небольшим полезным нагрузкам, с которыми приходится сталкиваться. При меньшей длине кода матрица проверки четности (ПЧ) кодов LDPC не становится более разреженной; свойство «низкой плотности» теряется, и становится неизбежным наличие коротких циклов в ПЧ-матрице. Как следствие, производительность алгоритма декодирования, основанного на распространении доверия (BP), также известного как sum-product (SP), становится низкоэффективной. В такой ситуации предлагается представить алгоритм BP в виде нейронной сети (НС), что позволяет адаптивно взвешивать сообщения, которыми обмениваются в процессе декодирования.
Рассматривается линейный блочный код C длиной n и разрядом k. Связанная матрица генератора размером k × n и соответствующая матрица проверки четности размером (n – k) × n обозначаются как G и H соответственно. Матрица проверки четности может быть представлена в виде двудольной графовой модели, называемой графом Таннера, определенного типа факторного графа (ФГ). Исследование способа идентификации циклов в графах Таннера LDPC кодов на основе пересечений коротких замкнутых структур в протографах было рассмотрено в работе [7]. Такое представление обеспечивает эффективное итеративное декодирование на основе классических алгоритмов передачи сообщений, таких как BP. Этот алгоритм направлен на то, чтобы сходиться к передаваемому кодовому слову путем итеративного обмена «предположениями» между узлами графа о вероятных значениях полученных битов кодового слова. Обычно обмениваемые сообщения связаны с логарифмическими коэффициентами правдоподобия (LLR) полученных битов, и правило обновления sum-product может быть применено к различным узлам, используя следующие уравнения:
– правило обновления SP, примененное к переменному узлу i для вычисления сообщения для контрольного узла j:
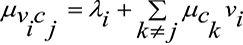 ,(1)
,(1)
где 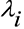 – предшествующее значение LLR, полученное переменным узлом i,
– предшествующее значение LLR, полученное переменным узлом i,
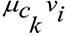 – сообщения, полученные переменным узлом от соседних контрольных узлов k.
– сообщения, полученные переменным узлом от соседних контрольных узлов k.
– правило обновления SP, применяемое к контрольному узлу j для вычисления сообщения для переменного узла i:
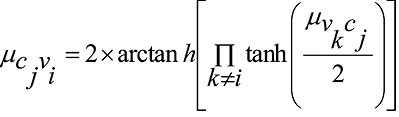 ,(2)
,(2)
где 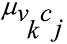 – сообщения, полученные контрольным узлом j от соседних переменных узлов k;
– сообщения, полученные контрольным узлом j от соседних переменных узлов k;
– правило обновления SP, применяемое к переменному узлу i для вычисления бита i для последующего LLR:
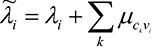 .(3)
.(3)
Поскольку ФГ не является циклическим, необходимо применить итеративное декодирование путем передачи сообщений туда и обратно между переменным и контрольным узлами, используя уравнения (1) и (2), прежде чем прийти к удовлетворительному решению. Алгоритм нейросетевого распространения доверия (NBP) предлагает научиться взвешивать сообщения и вводить LLR уравнений (1), (2) и (3), чтобы уменьшить негативное влияние коротких циклов на конечную производительность декодирования.
По мере увеличения количества слоев в нейронной сети улучшаются возможности обработки данных моделей. Искусственная нейронная сеть состоит из нескольких нейронов, соединяющих друг друга с другими ребрами. Нейронные сети обеспечивают входной уровень, несколько скрытых слоев и выходной слой, что позволяет выполнять более точные и сложные задачи определения и классификации образов. Поскольку нейронная сеть содержит несколько скрытых слоев, она называется глубокой нейронной сетью. В моделях глубокой нейронной сети (ГНС) каждый нейрон и связанные с ним ребра имеют свои характерные особенности. На каждом нейроне есть функция активации и параметр смещения, а также параметр веса на ребре, соединенном с нейроном. Функция активации представляет собой нелинейное преобразование выходного сигнала нейрона. Входной сигнал умножается на вес, прибавляется к смещению, а затем производится для получения активного выходного сигнала. В ГНС вес и смещение силы используются для контроля связей между нейронами и смещения нейронов. Функции активации, вес и смещения в ГНС взаимодействуют друг с другом, и, регулируя их, можно контролировать силу связей, смещений и выходных результатов между нейронами, тем самым достигая обучения и прогнозирования нейронной сети.
Предлагается архитектура НС для выполнения алгоритма NBP, применяемого для декодирования линейных блочных кодов. В предлагаемом способе принимающему устройству больше не требуется предварительное знание используемой схемы кодирования. Как следствие, ему необходимо изучить как топологию ФГ, так и вес NBP. Предлагаемый декодер основан на пользовательской архитектуре ячеек рекуррентной нейронной сети (РНС), которая использует механизмы распределения веса и стробирования. Сначала правила SP будут описаны как эффективные матричные операции для универсальных линейных блочных кодов. Затем предлагаемые операции будут использоваться для РНС.
На каждой итерации NBP декодер запускается путем обновления сообщений из переменных в контрольные узлы 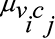 , следуя рассчитанному по весу выражению (1) (входные сообщения, полученные от контрольных узлов
, следуя рассчитанному по весу выражению (1) (входные сообщения, полученные от контрольных узлов 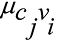 , инициализируются значением 0 на первой итерации). Это вычисление может быть реализовано с использованием плотного слоя НС, как показано на рис. 1, где Nпеременных и Nпроверочных обозначают количество переменных и контрольных узлов в ФГ, ω(Aj) – нелинейная функция, применяемая к параметрам факторного графа для представления как механизмов стробирования (т. е. бинарного выбора), так и механизмов взвешивания. Например, если ω(Aj) определено как ступенчатая функция, то вычислительный график будет воспроизводить стандартный алгоритм BP с двоичными весами. Коэффициенты βi не должны проходить через функцию ω, потому что нет необходимости в сокращении каких-либо входных данных.
, инициализируются значением 0 на первой итерации). Это вычисление может быть реализовано с использованием плотного слоя НС, как показано на рис. 1, где Nпеременных и Nпроверочных обозначают количество переменных и контрольных узлов в ФГ, ω(Aj) – нелинейная функция, применяемая к параметрам факторного графа для представления как механизмов стробирования (т. е. бинарного выбора), так и механизмов взвешивания. Например, если ω(Aj) определено как ступенчатая функция, то вычислительный график будет воспроизводить стандартный алгоритм BP с двоичными весами. Коэффициенты βi не должны проходить через функцию ω, потому что нет необходимости в сокращении каких-либо входных данных.
Поскольку декодирование BP является итеративным алгоритмом, вышеупомянутые операции должны повторяться несколько раз для достижения хорошей производительности. РНС может использоваться для выполнения такого итеративного декодирования в рамках НС.
Активация нейрона в слое, отличном от входного, представляет собой сумму произведений его входных данных и параметров веса, соответствующих соединениям, которые вводят эти входные данные. Рассмотрим j-й нейрон в скрытом слое и примем j = 2. Если входной сигнал равен (1,1; 2,4; 3,2; 5,1; 3,9), а конечный выходной параметр равен (0,52; 0,75; 0,97), если веса, заданные для нейрона второго скрытого слоя, задаются вектором (–0,33; 0,07; –0,45; 0,13; 0,37), то активация будет произведена следующим образом:
(–0,33; 1,1) + (0,07; 2,4) + (–0,45; 3,2) + (0,13; 5,1) + (0,37; 3,9) = 0,471.(4)
Теперь добавим к этому необязательное смещение или пороговое значение, например, 0,679, чтобы получить 1,15, и используем сигмовидную функцию, заданную I(1 + exp(–x)), при x = 1,15 выходной сигнал этого нейрона скрытого слоя будет равен 0,7595. Если вычисленный выходной параметр также оказывается равным (0,61; 0,41; 0,57; 0,53), в то время как желаемое значение равно (0,52; 0,25; 0,75; 0,97). Очевидно, существует несоответствие между желаемым и вычисленным. Различия по компонентам приведены в векторе (–0,09; –0,16; 0,18; 0,44). Этот вектор используется для формирования другого вектора, где каждый компонент является произведением компонента ошибки, соответствующего вычисленного компонента шаблона и дополнения последнего относительно 1. Для первого элемента ошибка равна –0,09, вычисленный элемент эталонного значения равен 0,61, а его дополнение равно 0,39. Умножая их вместе, получаем –0,02. Аналогично вычисляя другие компоненты, получаем вектор, равный (–0,02; –0,04; 0,04; 0,11). Теперь необходимы веса соединений между вторым нейроном в скрытом слое и различными выходными нейронами. Если эти веса заданы вектором (0,85; 0,62; –0,10; 0,21), то ошибка второго нейрона в скрытом слое может быть вычислена с использованием его выходных данных. Ошибка равна:
0,7595((1 – 0,7595)(0,85; –0,02) + (0,62; –0,04) + (–0,045)(–0,10; 0,4) + (0,21; 0,11)) = –0,0041.(5)
Далее необходим параметр скорости обучения для этого уровня. Теперь оно установлено равным 0,2. Умножив этот выходной сигнал второго нейрона на параметр скорости обучения, равный 0,2 в скрытом слое, получим 0,1519. Каждый из компонентов вектора (–0,02; –0,04; 0,04; 0,11) теперь умножается на 0,1519, что является последним достигнутым вычислением. Результатом является вектор, который корректирует веса соединений, идущих от второго нейрона в скрытом слое к выходным нейронам. Эти значения заданы в векторе (–0,003; –0,006; 0,006; 0,017). После добавления этих корректировок веса, которые будут использоваться в следующем цикле для связей между вторым нейроном в скрытом слое и выходными нейронами, становятся весами в векторе (0,847; 0,614; ... 0,094; 0,227).
На рис. 2 предлагается структурированная ячейка РНС, адаптированная для выполнения нейросетевого BP-декодирования линейных блочных кодов.
Ячейка рекуррентной нейронной сети построена на основе двух типов обучаемых параметров веса:
– стробирующие веса: wG представляют топологию факторного графа и используются для соответствующего выбора сообщений на различных этапах процесса декодирования. Чтобы представить такое поведение при бинарном выборе, к этим весам применяется сигмоидальная функция активации σ;
– веса NBP: веса wΣ и wOUT используются для улучшения производительности схемы декодирования аналогично механизму NBP.
Все веса распределяются между различными итерациями РНС. Веса стробирования также распределяются внутри любой заданной итерации между различными операциями алгоритма BP. Структурированная архитектура НС гарантирует, что изученный алгоритм декодирования аналогичен NBP, но позволяет изучать топологию ФГ. В предлагаемой архитектуре вышеупомянутые функции ω, θ, γ и ψ могут быть определены следующим образом:
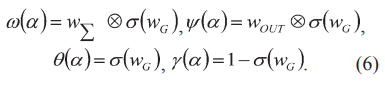
Система обработки сообщений выбирает сообщения, используя модифицированную функцию обработки σ(wG). Эта функция в значительной степени действует как сигмовидная функция, но обеспечивает лучшее обратное распространение градиента в режиме насыщения сигмоидной функции, тем самым улучшая обучаемость вентиля (за счет дополнительных обучаемых параметров). Можно отметить, что выбранная архитектура взвешивает сообщения только на определенных этапах. Использование разных параметров веса перед операциями и OUT кажется эффективным.
Чтобы оценить производительность предлагаемой ячейки РНС, в TensorFlow определяется сквозная модель НС со следующими настраиваемыми слоями. Системная модель показана на рис. 3, где ячейки, выделенные серым цветом, не поддаются обучению, а белым цветом – поддаются.
В данной системной модели рекуррентной нейронной сети подаваемые на вход информационные слова x кодируются с использованием систематических версий кодов Боуза – Чоудхури – Хоквингема БЧХ (15,11) или БЧХ (15,7), применяется двоичная фазовая модуляция (BPSK), затем символы кодового слова проходят через канал с аддитивным белым гауссовским шумом (АБГШ). С учетом используемой модуляции и канала вычисляется LLR принятых выборок.
Предварительная обработка LLR: для облегчения обучения РНС значения LLR нормализуются до диапазона [–1, +1] в соответствии с максимальным абсолютным значением LLR в каждом кодовом слове. Затем LLR передается в соответствии с заданным числом итераций. К нормализованным кодовым словам применяется итерационный алгоритм расчета весовых коэффициентов. Это могло бы позволить НС компенсировать недостаточный диапазон нормализации кодовых слов, с одной стороны, а также внести разнообразие в итерации РНС, изменив баланс между входными данными LLR и сообщениями из предыдущей итерации, с другой стороны. Предлагаемая закрытая ячейка NBP РНС используется для декодирования принятых кодовых слов. Нейросетевой алгоритм BP должен изучить схему кодирования, используемую в источнике.
При обработке выходных данных вместо извлечения только результата последней итерации BP выходные данные всех итераций объединяются повторно с использованием взвешенной суммы. Таким образом, уровень РНС используется в конфигурации «многие ко многим». Такой подход упрощает обратное распространение градиента, вводя его обратно на каждой итерации BP. Это также позволяет системе придавать большее значение результатам итерации, которые являются наиболее надежными с точки зрения опыта обучения. Зная положение систематических битов кода, затем применяется уровень определяемой выборки для подбора этих битов, и применяется сигмовидная функция для сжатия декодированного логарифмического коэффициента правдоподобия либо до 0, либо до 1.
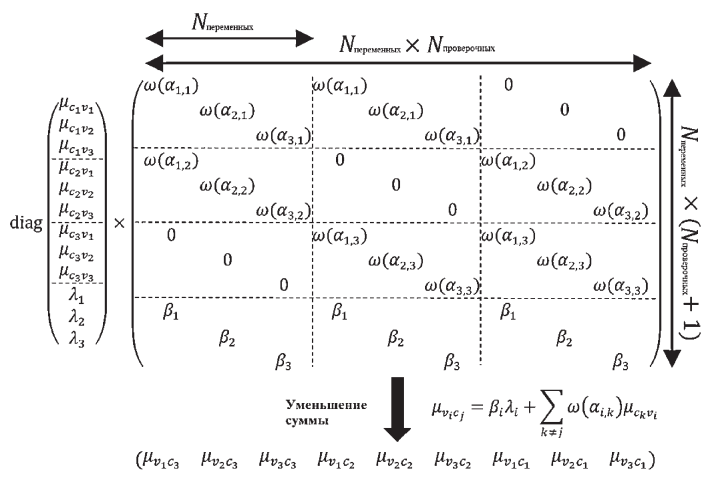
Рис. 1. Реализация взвешенной функции уравнения (1) с использованием плотного слоя
Примечание: составлено авторами по источнику [8].
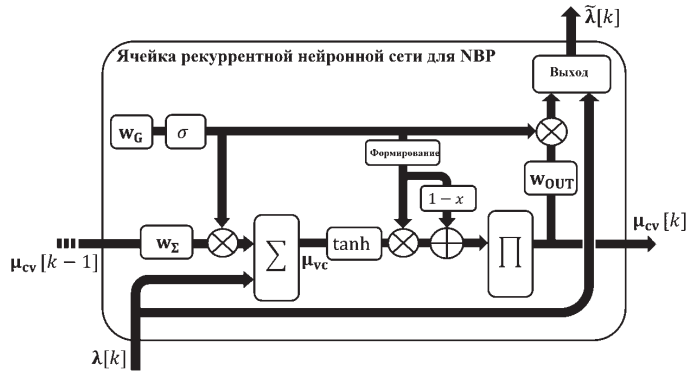
Рис. 2. Предлагаемая закрытая ячейка РНС для выполнения NBP-декодирования линейных блочных кодов
Примечание: составлено авторами по источнику [8].
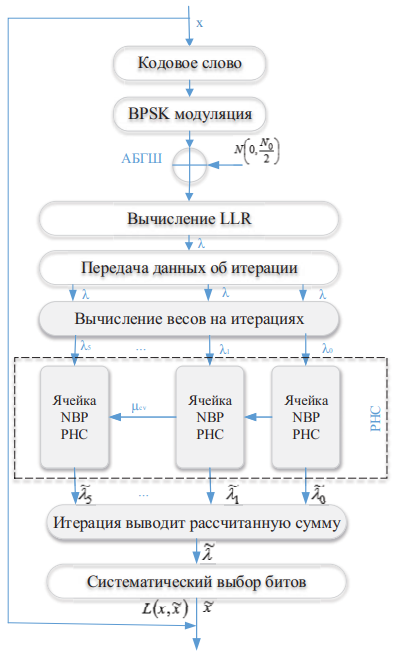
Рис. 3. Системная модель рекуррентной нейронной сети
Примечание: составлено авторами на основании данных, полученных в исследовании.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Структура автоматического кодирования обеспечивает простой процесс обучения, поскольку функция потерь может быть вычислена как двоичная перекрестная энтропия между исходными информационными словами x и декодированными словами x˜. Для обоих кодов обучение выполняется с использованием случайно выбранных информационных битов, разделенных на слова размером k. Количество слов, используемых для обучения, в 10 раз превышает общее количество возможных слов, 2k. Уровень шума, используемый на этапе обучения, зафиксирован на уровне 4 дБ. Механизм регуляризации со смещением ℓ2 применяется для ограничения полученных весовых коэффициентов NBP, которые находятся слишком далеко от 1.
Модель оценивалась на наборе данных, состоящем из случайно выбранных слов. Для получения надежных результатов вместо фиксированного количества тестируемых слов было исправлено количество ошибок, которых необходимо достичь. Производительность лучшей модели среди 50 тренировок, обозначенной как «NBP РНС», сравнивается с базовыми показателями максимального правдоподобия (ML) и стандартного декодирования BP для обоих кодов, как показано на риc. 4.
Все кривые производительности отображаются в виде частоты ошибок блока (количество ошибочно декодированных кодовых слов среди всех обработанных кодовых слов).
Предлагаемая модель способна обучаться декодированию обоих кодов и превосходит стандартный алгоритм BP, особенно для кода БЧХ (15,7), где прирост производительности до 1 дБ значительно сокращает разрыв при декодировании с максимальным правдоподобием.
На рис. 5 приведена частота битовых ошибок для кода БЧХ с N = 15, а для БЧХ (15,7) и БЧХ (15,11) получено улучшение до 0,9 и 1,0 дБ соответственно.
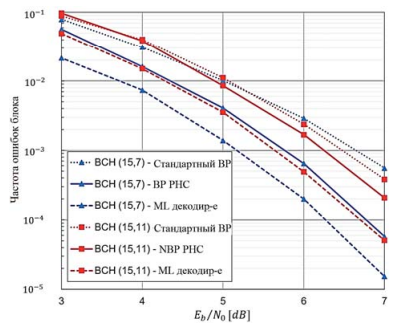
Рис. 4. Частота ошибок блока предложенной модели по сравнению со стандартными декодерами BP и максимального правдоподобия для кодов БЧХ (15,11) и БЧХ (15,7)
Примечание: составлено авторами на основании данных, полученных в исследовании.
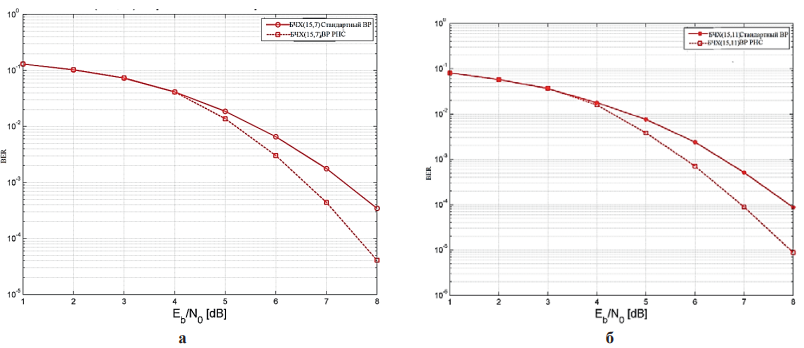
Рис. 5. Результаты BER для кода БЧХ: а – обученного с использованием матрицы проверки для алгоритмов стандартного BP; б – нейросетевого BP
Примечание: составлено авторами на основании данных, полученных в исследовании.
ЗАКЛЮЧЕНИЕ
Представлена эффективная архитектура РНС со стробированием для декодирования линейных блочных кодов. Эта архитектура улучшает процесс итеративного декодирования BP, используя подход нейросетевого BP, при котором на приемной стороне не требуется предварительных знаний об используемой схеме кодирования. Вычислительный граф разработан несложным, универсальным и масштабируемым для больших кодов. Основными преимуществами разработанной архитектуры являются:
– контролируемое количество обучаемых параметров и вычислений в нейронной сети благодаря распределению веса и эффективному вычислительному графу;
– структурированная архитектура, обеспечивающая применение алгоритма NBP для декодирования линейных блочных кодов;
– улучшенная производительность по сравнению со стандартным декодером BP благодаря применению нейросетевого алгоритма BP;
– повышенная гибкость декодера благодаря его возможностям обучения.
Декодер РНС может быть использован для повышения производительности и альтернативного снижения вычислительной сложности алгоритма декодирования коротких и средней длины кодов в беспроводных системах передачи информации.
Планируется изучение возможностей такой структурированной архитектуры для схемы декодирования больших кодов, где невозможно предоставить все кодовые слова в обучающем наборе данных.
Список литературы
1. Зинченко М. Ю., Левадний А. М., Гребенко Ю. А. Реализация LDPC декодера на ПЛИС и оптимизация потребляемой мощности // T-Comm: Телекоммуникации и транспорт. 2020. Т. 14, № 3. С. 4–10.
2. Хорошайлова М. В. Архитектура канального кодирования на основе ПЛИС для 5G беспроводной сети с использованием высокоуровневого синтеза // Вестник Воронежского государственного технического университета. 2018. Т. 14, № 2. С. 99–105.
3. Хорошайлова М. В. Архитектура для стохастических LDPC-декодеров c использованием эффективной площади кристалла на основе ПЛИС // Вестник Воронежского государственного технического университета. 2018. Т. 14, № 1. С. 95–100.
4. Башкиров А. В., Хорошайлова М. В., Демихова А. С. Разработка архитектуры слепого распознавания линейного блочного кодирования с использованием каскадной сети // Вестник Воронежского государственного технического университета. 2023. Т. 19, № 6. С. 130–137.
5. Башкиров А. В., Муратов А. В., Хорошайлова М. В. и др. Низкоплотностные коды малой мощности декодирования // Радиотехника. 2016. № 5. С. 32–37.
6. Silver D., Huang A., Maddison C. J. et al. Mastering the game of Go with deep neural networks and tree search // Nature. 2016. Vol. 529, no. 7587. P. 484–489.
7. Овинников А. А. Способ идентификации циклов в графах Таннера LDPC кодов на основе пересечений коротких замкнутых структур в протографах // Цифровая обработка сигналов. 2016. № 4. С. 26–30.
8. Mandic D. P., Chambers J. A. Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures and Stability. London : Wiley, 2001. 308 p.
Об авторах
А. А. ПироговРоссия
кандидат технических наук, доцент
М. В. Хорошайлова
Россия
кандидат технических наук, доцент
Э. В. Сёмка
Россия
кандидат физико-математических наук, доцент
Рецензия
Для цитирования:
Пирогов А.А., Хорошайлова М.В., Сёмка Э.В. Разработка архитектуры нейросетевого декодирования, основанной на системах стробирования и распределения весовых коэффициентов. Вестник кибернетики. 2024;23(3):46-55. https://doi.org/10.35266/1999-7604-2024-3-6
For citation:
Pirogov A.A., Khoroshailova M.V., Syomka E.V. Development of a neural network decoding architecture based on gating and weight distribution systems. Proceedings in Cybernetics. 2024;23(3):46-55. (In Russ.) https://doi.org/10.35266/1999-7604-2024-3-6















