Перейти к:
Применение метода вейвлет-анализа данных для построения прогнозной модели
https://doi.org/10.35266/1999-7604-2024-3-9
Аннотация
Работа посвящена разработке модели прогнозирования цены на любой продукт на основе исследования входных данных с помощью метода вейвлет-анализа. Данный метод является удобным инструментом для обработки и преобразования различных типов исходных данных. Каждый элемент рыночного механизма связан с ценой, которая является основным критерием, воздействующим на спрос и предложение. Процессы планирования, стимулирования и управления экономической деятельностью на всех стадиях воспроизводства связаны с ценообразованием, и предвидение последствий принимаемых решений является достаточно важной задачей. В ходе проведенных экспериментов на данных из открытых источников были получены удовлетворительные результаты; установлено, что строить прогноз возможно не более чем на три последующих дня.
Ключевые слова
Для цитирования:
Чубарова О.В., Чубаров А.В., Ликсонова Д.И. Применение метода вейвлет-анализа данных для построения прогнозной модели. Вестник кибернетики. 2024;23(3):82-89. https://doi.org/10.35266/1999-7604-2024-3-9
For citation:
Chubarova O.V., Chubarov A.V., Liksonova D.I. Application of wavelet data analysis for forecast model development. Proceedings in Cybernetics. 2024;23(3):82-89. (In Russ.) https://doi.org/10.35266/1999-7604-2024-3-9
ВВЕДЕНИЕ
В настоящее время используется большое количество традиционных методов анализа для прогнозирования цен. К ним можно отнести методы анализа данных и машинного обучения (например, алгоритм градиентного бустинга, факторная регрессионная модель, метод корреляционно-регрессионного анализа и др.). Безусловно, такие методы имеют преимущества и недостатки. При рассмотрении процесса изменения цен ценовой ряд можно отнести к временному ряду. Одним из основных методов обработки такого ряда является спектральный анализ (Фурье-анализ), который позволяет охарактеризовать частотный состав исследуемого сигнала [1][2]. Недостатком Фурье-анализа является то, что частотные компоненты носят глобальный характер в силу существования в пределах от –∞ до +∞, это условие естественным образом ограничивает его использование на практике. Существует форма кратковременного преобразования Фурье. Однако и у этой формы существует недостаток, происходящий от небезызвестного принципа Гейзенберга. Поэтому решением задачи исследования временных рядов могут стать преобразования с переменным разрешением, такие как вейвлет-преобразования [3]. Таким образом, основной задачей данной работы является моделирование временных рядов с применением математического аппарата вейвлет-анализа.
МАТЕРИАЛЫ И МЕТОДЫ
Сравнительно молодой термин «вейвлет» введен в середине 1980-х гг. в статье А. Гроссмана и Ж. Морле, посвященной анализу свойств сейсмических и акустических сигналов [3]. Сейчас это известно как «вейвлет-преобразование», которое переводит сигнал из временного представления в частотно-временное. При решении практических задач анализ различных зависимостей на основе вейвлетов получил широкое применение [4].
Анализ одномерного сигнала с помощью вейвлет-преобразования состоит в его разложении по базису. Базисные функции должны обладать определенными свойствами солитоноподобной функции (вейвлета) за счет масштабных изменений и переносов. Каждая из функций этого базиса характеризует как определенную пространственную (временную) частоту, так и ее локализацию в физическом пространстве (времени). Преобразование выполняется отдельно для различных сегментов сигнала во временной области. Базисные функции определены компактно, это позволяет говорить о финитности получаемых последовательностей.
В случае когда сигнал представляет собой нестационарный случайный процесс, для задач анализа и синтеза, оптимизации параметров моделей сигналов и выделения сигналов на фоне шумов различного происхождения целесообразно применить вейвлет-преобразование. Благодаря высокому разрешению во временной области возможно выделять и анализировать импульсные составляющие, проектируя на основе полученных данных различные графические модели, удобные для восприятия [5].
Для временного ряда с помощью методов вейвлет-анализа необходимо получить количественные и качественные оценки, характеризующие нестационарность (хаотичность) исследуемого процесса, затем построить авторегрессионную математическую модель типа ARMA [6] для коэффициентов разложения, сделать их прогноз, после чего выполнить вейвлет-реконструкцию для предсказания исходного сигнала.
В первую очередь необходимо выполнить вейвлет-разложение исходного временного ряда. В результате этого на каждом уровне получаемый на предыдущем шаге низкочастотный сигнал разделяется на низкочастотную и высокочастотную части.
Исходный сигнал (обозначим его как x) после разложения на N слоев можно представить следующим образом:
x = D1 + D2 + ... + DN + AN , (1)
где D1, D2, …, DN – это первый, второй и другие N слоев соответственно (высокочастотные сигналы);
AN – это низкочастотный сигнал, полученный путем разложения N-го слоя.
Таким образом, необходимо получить прогнозные значения D1, D2, …, DN и AN, после чего выполнить вейвлет-реконструкцию для предсказания исходного сигнала [7].
Представим блок-схему работы алгоритма прогнозирования (рис. 1).
Рассмотрим последовательность шагов для разложения по методу вейвлет-анализа.
- Необходимо разложить выбранные данные с использованием вейвлет-анализа. Выбираем в качестве вейвлет-функции вейвлеты Добеши с n = 4, которые являются достаточно известными типами и используются во многих практических приложениях. Вейвлеты порядка N (dbN) отличны от нуля лишь на интервале длиной (2N – 1) и имеют 2Nотличных от нуля коэффициентов фильтров [8]. Количество уровней разложения – 2.
- Создаем и восстанавливаем модель ARMA для каждого коэффициента слоя.
- По построенным моделям определяем вейвлет-коэффициенты, для чего определяем количество шагов, которое следует предсказать каждой модели ARMA. Для этого проверяем количество коэффициентов после вейвлет-разложения всех исходных данных и находим разницу.
- Для предсказания исходного сигнала производим вейвлет-реконструкцию.
В результате выполнения данной последовательности шагов получаем модель, которая позволит построить необходимый прогноз временного ряда.
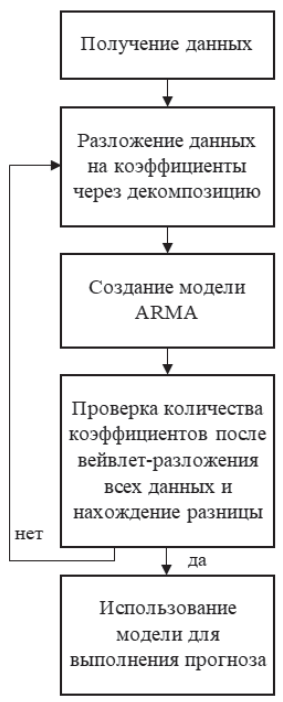
Рис. 1. Блок-схема работы алгоритма прогнозирования
Примечание: составлено авторами на основании разработанного алгоритма.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В качестве исходной информации для исследования были взяты данные из открытых источников, в частности цена закрытия акций на торгах некоторых компаний. Были сформированы обучающая и тестовая выборки.
Из исходной выборки выделим значения «цена закрытия» и разделим их на тиккеры. Для каждого тиккера выделяем обучающую выборку и 5 точек для построения прогноза. На обучающей выборке применяем вейвлет-преобразование с уровнем глубины 2, в результате чего получаем коэффициенты разложения D1, D2, A2, которые затем используем для настройки авторегрессионной модели ARMA.
Покажем пример полученной модели по обучающей выборке для тиккера «CLL» (рис. 2). Значение по оси абсцисс – номер точки (соответствует временному промежутку равному суткам), по оси ординат – значение цены закрытия.
Построим прогноз цены закрытия на 5 дней вперед по полученной модели. Результаты прогнозирования и реальные значения цены представлены в табл. 1: показаны реальные значения из теста (real), предсказанные (predict), сигнал рассогласования (err) и относительная ошибка в процентах (err_rate).
Приведем на рис. 3 предсказание на тестовой выборке (укрупненно для 5 точек) по модели ARMA, предсказанные точки обозначены кружочками, реальные – звездочками.
Было проведено моделирование на разных тиккерах и для разных периодов прогнозирования. Полученные результаты позволяют говорить об эффекте прогнозирования модели на небольшие промежутки времени, то есть чем длительней период прогнозирования, тем больше растет ошибка. В результате было принято решение не строить прогноз на период более чем 3 дня.
Покажем на примере тиккера «A-share», как выглядят модели ARMA для глубины равной 2 (рис. 4–6). На рисунках пунктирной линией представлены истинные данные, сплошной – значения модели.
Анализируя модели вейвлет-коэффициентов, можно понять необходимость фильтрации исходной последовательности. Цель состоит в том, чтобы подавить шумовую часть сигнала и восстановить основной тренд.
При вейвлет-анализе сигнал разделяется на сглаженный (аппроксимирующие коэффициенты) и шумовой (детализирующие коэффициенты). К шумовой части целесообразно применить вейвлет-фильтрацию. Поскольку шумовая компонента больше отражается в детализирующих коэффициентах Dj, обрабатывают обычно их. Самый простой способ удаления шума – придать нулевые значения коэффициентам, меньшим некоторой пороговой величины. Эта процедура называется пороговой обработкой или трешхолдингом коэффициентов [8].
Полученные детализирующие вейвлет-коэффициентов D1, D2, …, DN – 2, DN – 1 обнуляют все положительные (отрицательные) значения, имеющие амплитуду, меньшую (большую), чем некоторые положительные (отрицательные) пороги, устанавливаемые симметрично относительно нулевого уровня [8]. Для задачи фильтрации лучшим вариантом будет ситуация, когда остальные элементы векторов остаются без изменения, то есть реализуется так называемый жесткий порог. При решении практических задач также можно столкнуться с использованием мягкого порога, когда элементы последовательностей, находящиеся вне ограниченной порогами полосы, сдвигаются по направлению к нулевому уровню на величину высоты порога.
Продемонстрируем результат применения фильтрации исходной последовательности и покажем результат прогнозирования на 3 дня. На рис. 7 представлена полученная модель для тиккера «XOM».
Результаты прогнозирования и реальные значения цены для выбранных данных представлены в табл. 2.
Приведем на рис. 8 предсказание на тестовой выборке (укрупненно для 3 точек).
Видно, что применение трешхолдинга позволило уменьшить ошибку прогнозирования. Высокой точности прогнозирования временного ряда, безусловно, не ожидается, но важным является отслеживание тенденции роста или падения цены закрытия, что вполне отслеживается в прогнозе.
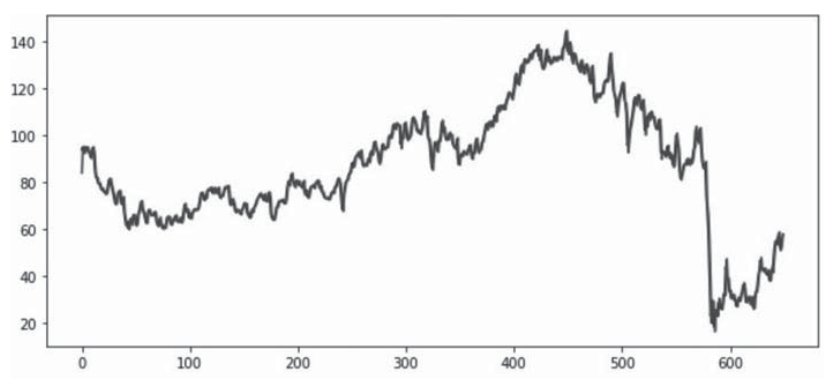
Рис. 2. Модель прогнозирования тиккера «CLL» с использованием вейвлет-анализа
Примечание: составлено авторами на основании данных, полученных в исследовании.
Таблица 1
Результаты прогнозирования
|
№ |
real |
predict |
err |
err_rate |
|
0 |
28,56 |
28,80 |
0,24 |
0,86 |
|
1 |
29,30 |
28,75 |
–0,54 |
1,86 |
|
2 |
27,75 |
29,06 |
1,32 |
4,75 |
|
3 |
27,82 |
29,17 |
1,35 |
4,87 |
|
4 |
27,94 |
29,20 |
1,26 |
4,50 |
Примечание: составлено по модели ARMA.
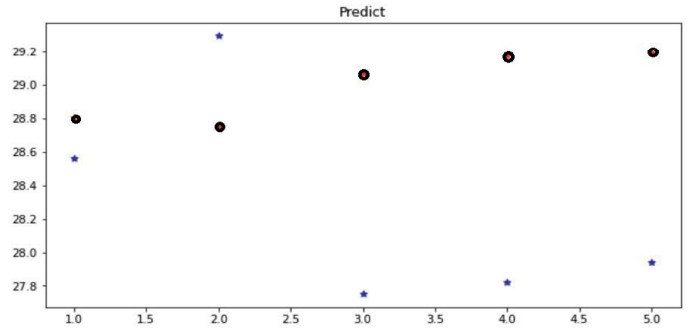
Рис. 3. Предсказание на тестовой выборке по модели ARMA
Примечание: составлено авторами на основании данных, полученных в исследовании.
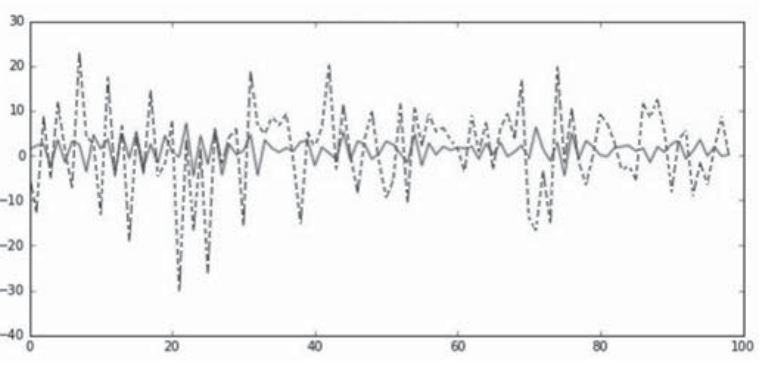
Рис. 4. Модель ARMA для слоя коэффициента D1
Примечание: составлено авторами на основании данных, полученных в исследовании.
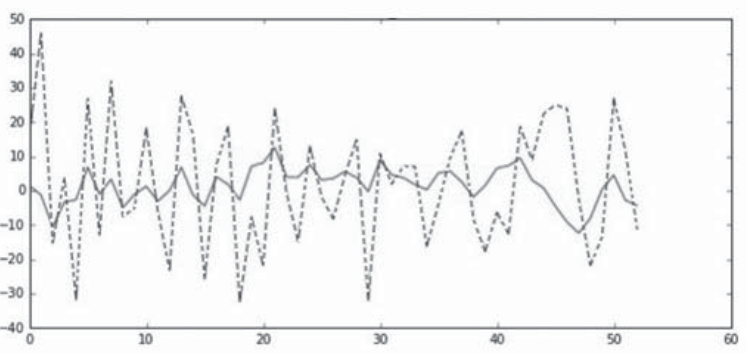
Рис. 5. Модель ARMA для слоя коэффициента D2
Примечание: составлено авторами на основании данных, полученных в исследовании.
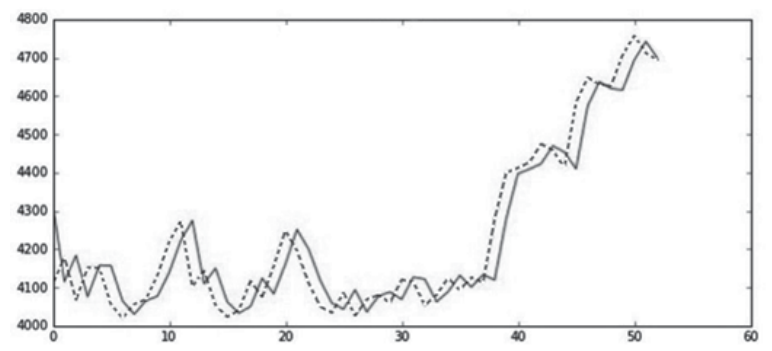
Рис. 6. Модель ARMA для слоя коэффициента A2
Примечание: составлено авторами на основании данных, полученных в исследовании.
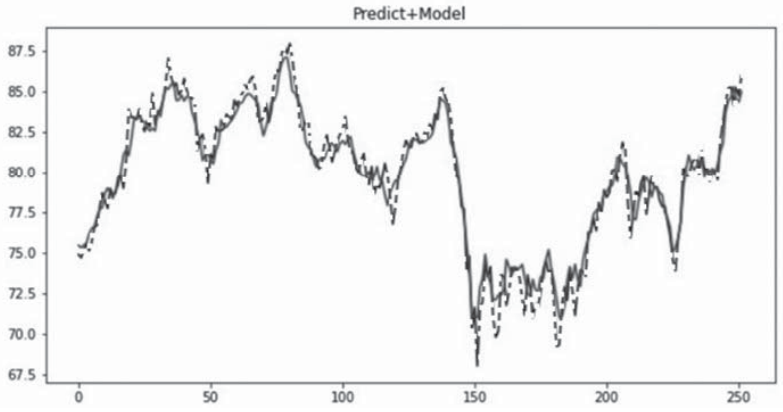
Рис. 7. Модель с фильтрацией для тиккера «XOM»
Примечание: составлено авторами на основании данных, полученных в исследовании.
Таблица 2
Результаты прогнозирования для тиккера «XOM»
|
№ |
real |
predict |
err |
err_rate |
|
0 |
87,05 |
87,53 |
0,47 |
0,55 |
|
1 |
86,10 |
87,75 |
1,66 |
1,92 |
|
2 |
85,04 |
87,23 |
2,18 |
2,57 |
Примечание: составлено по модели ARMA.
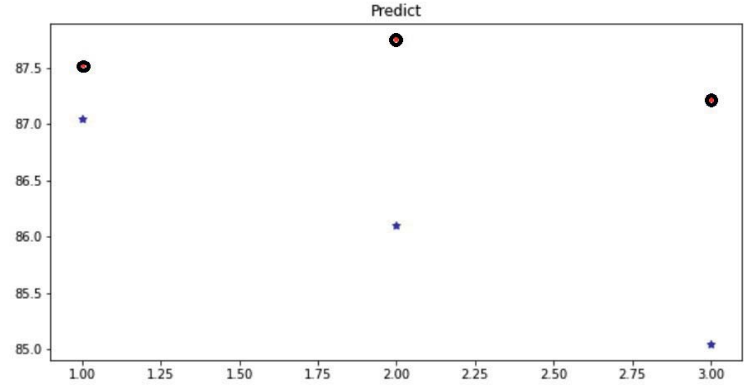
Рис. 8. Предсказание на тестовой выборке для тиккера «XOM»
Примечание: составлено авторами на основании данных, полученных в исследовании.
ЗАКЛЮЧЕНИЕ
Проведя исследования данного подхода на разных тиккерах за разный период, времени можно сделать следующие выводы:
− использование вейвлет-анализа для временных рядов является эффективным инструментом;
− модель прогнозирования имеет более высокую точность прогнозов на небольших временных промежутках;
− при вейвлет-реконструкции для предсказания исходного сигнала целесообразно использовать фильтрацию.
В перспективе для моделирования вейвлет-коэффициентов каждого слоя после вейвлет-разложения можно попробовать иные методы, например, нейронные сети.
Список литературы
1. Латыпова Н. В., Тучинский Л. И. Ряды Фурье. Ижевск : Удмуртский университет, 2011. 80 с.
2. Жук В. В., Натансон Г. И. Тригонометрические ряды Фурье и элементы теории аппроксимации. Л. : Изд-во ЛГУ, 1983. 188 с.
3. Grossman A., Morlet J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape // SIAM Journal on Mathematical Analysis. 1984. Vol. 15, no. 4. P. 723–736.
4. Нагорнов О. В., Никитаев В. Г., Простоквашин В. М. и др. Вейвлет-анализ в примерах. М. : НИЯУ МИФИ, 2010. 120 с.
5. Новиков И. Я., Протасов В. Ю., Скопина М. А. Теория всплесков : моногр. М. : Физматлит, 2005. 615 с.
6. Афанасьев В. Н., Юзбашев М. М. Анализ временных рядов и прогнозирование. М. : Финансы и статистика, 2001. 228 с.
7. Анализ и модели временных рядов. URL: https://www.statmethods.ru/statistics-metody/modelivremennykh-ryadov/ (дата обращения: 15.05.2024).
8. Петров Г. А., Шуранов Е. В. Практика использования вейвлет-анализа в дефектоскопии. СПб. : Балт. гос. техн. ун-т, 2012. 64 с.
Об авторах
О. В. ЧубароваРоссия
кандидат технических наук, доцент
А. В. Чубаров
Россия
кандидат технических наук
Д. И. Ликсонова
Россия
кандидат технических наук
Рецензия
Для цитирования:
Чубарова О.В., Чубаров А.В., Ликсонова Д.И. Применение метода вейвлет-анализа данных для построения прогнозной модели. Вестник кибернетики. 2024;23(3):82-89. https://doi.org/10.35266/1999-7604-2024-3-9
For citation:
Chubarova O.V., Chubarov A.V., Liksonova D.I. Application of wavelet data analysis for forecast model development. Proceedings in Cybernetics. 2024;23(3):82-89. (In Russ.) https://doi.org/10.35266/1999-7604-2024-3-9















