Перейти к:
Оценка минимального достижимого уровня боковых лепестков функции неопределенности радиоимпульсных последовательностей
https://doi.org/10.35266/1999-7604-2024-3-11
Аннотация
В радиолокации и связи широко используются сложные сигналы, что определяет актуальность синтеза, исследования и оптимизации подобных сигналов. Целью статьи является получение расчетных формул оценки минимальной границы достижимого уровня боковых лепестков нулевого сечения функции неопределенности дискретно кодированных радиоимпульсных последовательностей. Введено понятие коэффициента оптимальности, показывающего превышение уровня боковых лепестков над потенциально достижимым минимальным значением. Показано, что радиоимпульсные последовательности на основе кодов Баркера являются оптимальными по критерию минимального уровня боковых лепестков нулевого сечения функции неопределенности. Приведены результаты проведенного анализа оптимальности многофазных радиоимпульсных последовательностей на основе кода Фрэнка, многофазных последовательностей на основе кода Чу и фазоманипулированных М-последовательностей. Полученные результаты могут быть использованы в радиолокации и связи.
Ключевые слова
Для цитирования:
Дёмко А.И., Алмазова Е.Г. Оценка минимального достижимого уровня боковых лепестков функции неопределенности радиоимпульсных последовательностей. Вестник кибернетики. 2024;23(3):96-102. https://doi.org/10.35266/1999-7604-2024-3-11
For citation:
Dyomko A.I., Almazova E.G. Assessment of minimum achievable sidelobes level of ambiguity function for radio pulse sequences. Proceedings in Cybernetics. 2024;23(3):96-102. (In Russ.) https://doi.org/10.35266/1999-7604-2024-3-11
ВВЕДЕНИЕ
В радиолокации, радионавигации и электрической связи широко применяются сложные сигналы, имеющие произведение длительности на ширину спектра больше единицы. Способность совместного разрешения по дальности и скорости определяется функцией неопределенности сигнала [1], которая характеризует степень отличия сигнала от своих копий, сдвинутых по времени и частоте во всем диапазоне возможных значений. Функция неопределенности характеризуется областью сильной корреляции (главный максимум) и областью слабой корреляции (боковые лепестки). Наличие боковых лепестков является нежелательным фактором, ухудшающим качество решения радиолокационных, радионавигационных и связных задач. В связи с этим актуальной является оценка оптимальности сигнала с точки зрения степени близости уровня боковых лепестков функции неопределенности к минимально достижимой величине.
МАТЕРИАЛЫ И МЕТОДЫ
Для радиотехнических систем, обработка сигнала в которых позволяет использовать несколько периодов повторения, можно использовать периодическую функцию неопределенности (ФН, ПФН), существуют сигналы с нулевым уровнем боковых лепестков нулевого сечения ПФН (сигналы с идеальными периодическими корреляционными свойствами) [2]. При обработке одного периода сигнала следует рассматривать импульсную (одиночную) ФН (1), уровень боковых лепестков нулевого сечения которой ненулевой и зависит от конкретного сигнала.
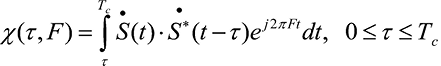 ,(1)
,(1)
где 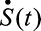 – комплексная форма представления сигнала;
– комплексная форма представления сигнала;
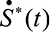 – комплексно-сопряженный сигнал;
– комплексно-сопряженный сигнал;
τ – временной сдвиг;
F – частотный сдвиг;
Тс – длительность сигнала.
Для примера на рис. 1 приведено тело неопределенности (трехмерное графическое изображение импульсной ФН) многофазной радиоимпульсной последовательности на основе кода Фрэнка из 64 элементов [3, 4].
Нормирование графика выполнено относительно начала координат x(0,0). Центр изображения (τ = 0, F = 0) соответствует главному максимуму ФН, где оба сигнала в подынтегральном выражении (1) максимально похожи друг на друга. Остальная область тела неопределенности меньшего уровня содержит боковые лепестки (в идеальном случае должны отсутствовать), характеризующие степень непохожести сигналов подынтегрального выражения (1) при отдалении от начала координат (τ ≠ 0, F ≠ 0). Наблюдается сложная структура боковых лепестков во всем интервале возможных временных задержек и частотных сдвигов (1).
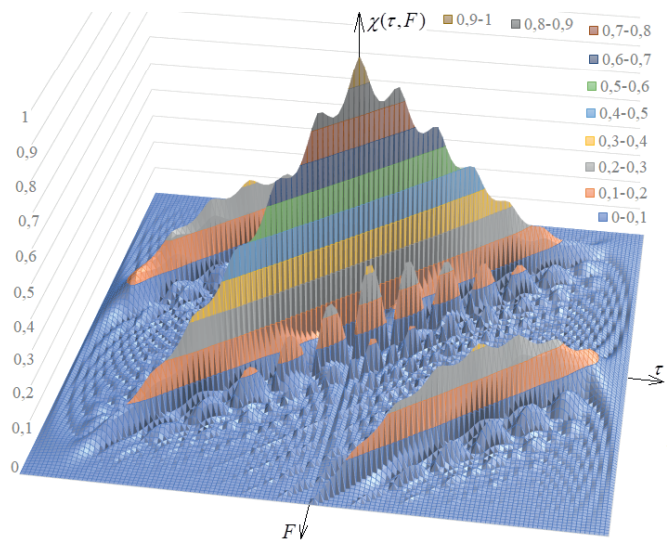
Рис. 1. Огибающая нормированного тела неопределенности сигнала на основе кода Фрэнка для последовательности из 64 элементов
Примечание: составлено авторами на основании данных, полученных в исследовании.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Определим нижнюю оценку уровня боковых лепестков нулевого сечения ФН, ниже которой уровень боковых лепестков получить невозможно для дискретно кодированных сигналов в виде радиоимпульсных последовательностей.
Радиоимпульсная последовательность из N радиоимпульсов:
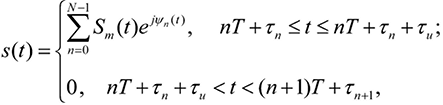 (2)
(2)
где Sm(t) – амплитуда радиоимпульса (возможна внутриимпульсная амплитудная, частотная или фазовая модуляция);
n – порядковый номер радиоимпульса;
Т – период следования радиоимпульсов;
ψn(t) – начальная фаза n-го радиоимпульса;
τn – сдвиг радиоимпульса относительно тактового (nT) момента времени;
τи – длительность радиоимпульса;
N – число радиоимпульсов в последовательности.
Tc = NT. (3)
Можно не ограничивать вид последовательности, допуская как однородные последовательности (следующие с одинаковым сдвигом радиоимпульсов относительно предыдущих, с модуляцией одного параметра, например начальной фазы радиоимпульсов), так и различные варианты неоднородных и разнопараметрических радиоимпульсных последовательностей.
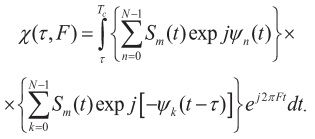 .(4)
.(4)
Найдем значения ФН при нулевом частотном сдвиге F (нулевое сечение функции неопределенности) при двух значениях сдвига по оси задержек:
а) нулевом (τ = 0), когда при вычислении интеграла (4) пересекаются все радиоимпульсы с одинаковыми номерами;
б) максимальном (τ = NT – T), когда пересекаются только последний радиоимпульс исходной последовательности с первым радиоимпульсом задержанной последовательности.
Значение функции неопределенности при нулевом (τ = 0) временном сдвиге:
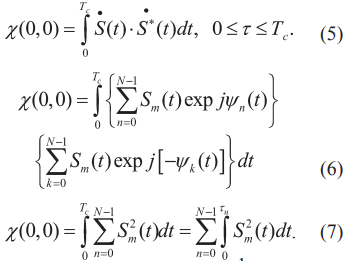
Для получения замкнутых форм выражения (7) ограничимся рассмотрением вариантов радиоимпульсных последовательностей с прямоугольной огибающей радиоимпульсов:
Sm(t) = Sm = const,(8)
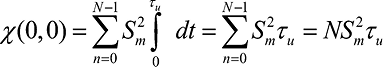 . (9)
. (9)
Абсолютное значение нулевого сечения функции неопределенности при нулевом временном сдвиге (9) пропорционально энергии радиоимпульса и числу радиоимпульсов в последовательности.
Вычислим значение нулевого сечения функции неопределенности при максимальном временном сдвиге, когда пересекаются только два радиоимпульса:
τmax = (N – 1)T. (10)
При этом в подынтегральном выражении (6) исчезают суммы, поскольку ненулевым остается лишь интеграл от произведения последнего радиоимпульса первой последовательности с первым радиоимпульсом второй последовательности.
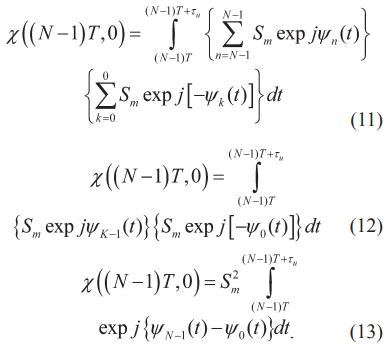
Дальнейшие преобразования интеграла (13) требуют конкретизации закона изменения фазы ψ(t), однако модуль интеграла от гармонической функции не зависит от аргумента гармонической функции, а определяется только пределами интегрирования, поэтому верхнюю оценку интеграла можно записать в виде:
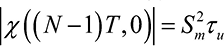 . (14)
. (14)
На основании выражений (9) и (14) можно произвести оценку нормированной величины бокового лепестка нулевого сечения функции неопределенности при сдвиге по оси задержки на величину (N – 1)T. Назовем эту величину коэффициентом оценки уровня боковых лепестков дискретно кодированных сигналов kN – 1.
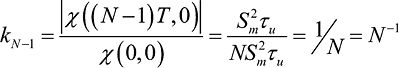 . (15)
. (15)
Расчетная формула для вычисления коэффициента оценки уровня боковых лепестков kK – 1 в логарифмических единицах.
kN – 1 = 201g(N– 1 ) = – 201g(N), дБ.(16)
Очевидно, что при любых меньших временных сдвигах kT (k ≠ N – 1) уровень боковых лепестков нулевого сечения функции неопределенности может как больше, так и меньше, но максимальное значение Mmax уровня боковых лепестков не может быть меньше, чем величина kN – 1. Для примера на рис. 2 изображено нормированное нулевое сечение ФН многофазной радиоимпульсной последовательности на основе кода Фрэнка из 256 элементов и коэффициент оценки уровня боковых лепестков k255.
Уровень боковых лепестков при таком числе элементов в последовательности составляет Mmax = –34 дБ. Боковые лепестки располагаются симметрично относительно главного максимума (вне зависимости от знака временной задержки), имеют сложную структуру и больший динамический диапазон (на рисунке 29 дБ – от минус 34 дБ до минус 63 дБ, хотя минимальные значения достигают минус 100 дБ).
Практическая полезность коэффициента оценки уровня боковых лепестков kN – 1 определяется двумя факторами:
а) kN – 1 определяет минимально достижимый уровень боковых лепестков нулевого сечения функции неопределенности при данном числе элементов в последовательности для данной радиоимпульсной последовательности;
б) kN – 1 соответствует значению уровня бокового лепестка при максимально возможной величине временного сдвига ± (N – 1)T.
Введем параметр, характеризующий величину отличия уровня боковых лепестков Mmax нулевого сечения функции неопределенности от коэффициента оценки уровня боковых лепестков kN – 1 и назовем его коэффициентом оптимальности kопт:
kопт = kN – 1 – Mmax = – 20lg(N) – Mmax , дБ.(17)
Коэффициент оптимальности большинства сигналов является отрицательным: чем больше по модулю его значение, тем в большей степени корреляционные свойства отличаются от оптимальных.
Известны бинарные коды Баркера [5] для 3, 4, 5, 7, 11 и 13 элементов в последовательности. Уровень боковых лепестков нулевого сечения функции неопределенности радиоимпульсных последовательностей на основе кодов Баркера совпадает с (16), поэтому для них коэффициент оптимальности kопт равен нулю, следовательно такие сигналы имеют минимально возможный уровень боковых лепестков.
На рис. 3 приведены зависимости коэффициента оптимальности для многофазных последовательностей на основе кода Фрэнка, многофазных последовательностей на основе кода Чу [6, 7] и псевдослучайных последовательностей максимальной длины (М-последовательностей) [8].
Как видно, для многофазных и фазоманипулированных радиоимпульсных последовательностей наиболее оптимальными (корреляционные параметры которых максимально приближаются к потенциально достижимым) являются последовательности небольшой длины. При увеличении длины последовательности становятся менее оптимальными, следовательно увеличиваются возможности для дополнительной оптимизации с целью улучшения корреляционных свойств сигналов [9].
Аналогично можно оценить степень отличия от оптимальных (по критерию максимального уровня боковых лепестков нулевого сечения функции неопределенности) для других радиоимпульсных последовательностей.
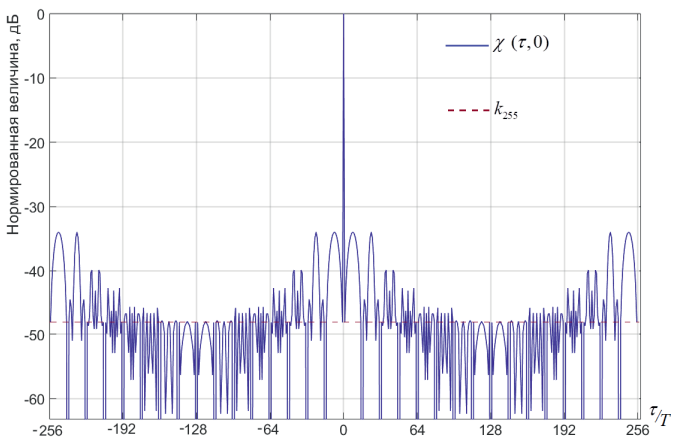
Рис. 2. Функция неопределенности многофазной радиоимпульсной последовательности на основе кода Фрэнка из 256 элементов и коэффициент оценки уровня боковых лепестков k255
Примечание: составлено авторами на основании данных, полученных в исследовании.
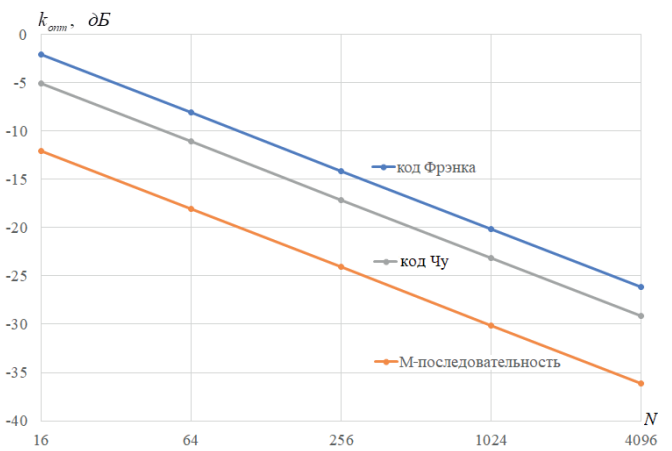
Рис. 3. Зависимость коэффициента оптимальности от числа элементов в последовательности
Примечание: составлено авторами на основании данных, полученных в исследовании.
ЗАКЛЮЧЕНИЕ
Для радиоимпульсных сигналов уровень бокового лепестка на границах максимальной задержки не зависит от вида модуляции, определяясь числом элементов в последовательности N.
Коэффициент оценки уровня боковых лепестков радиоимпульсной последовательности kN – 1 (18):
kN – 1 = – 201g(N), дБ(18)
определяет минимально-достижимый уровень боковых лепестков нулевого сечения функции неопределенности при данном числе элементов N в последовательности для данной радиоимпульсной последовательности и соответствует значению уровня бокового лепестка при максимально возможной величине временного сдвига ± (N – 1)T.
Коэффициент оптимальности kопт (19) характеризует отличие максимального уровня боковых лепестков радиоимпульсных последовательностей Mmax нулевого сечения функции неопределенности от потенциально достижимого:
kопт = kN – 1 – Mmax = – 201g(N) – Mmax , дБ.(19)
Коэффициент оптимальности kопт радиоимпульсных сигналов на основе бинарных кодов Баркера равен нулю, т. е. такие сигналы имеют минимально достижимый уровень боковых лепестков нулевого сечения функции неопределенности.
Для многофазных последовательностей на основе кода Фрэнка, многофазных последовательностей на основе кода Чу и М-последовательностей коэффициент оптимальности kопт уменьшается при увеличении числа радиоимпульсов N в последовательности со скоростью 6 дБ/окт.
Список литературы
1. Вакман Д. Е. Сложные сигналы и принцип неопределенности в радиолокации. М. : Сов. Радио, 1965. 304 c.
2. Кук Ч., Бернфельд М. Радиолокационные сигналы. Теория и применение / пер. с англ. ; под ред. В. С. Кельзона. М. : Сов. Радио, 1971. 567 с.
3. Дёмко А. И. О связи корреляционных свойств сигналов на основе кодов Фрэнка с погрешностями ихформирования // Вестник кибернетики. 2023. Т. 22, № 3. С. 23–31.
4. Frank R., Zadoff S., Heimiller R. Phase shift pulse codes with good periodic correlation properties (corresp.) // IRE Transactions on Information Theory. 1962. Vol. 8, no. 6. P. 381–382.
5. Дворников С. В., Дворников С. С., Марков Е. В. Модифицированные импульсные последовательности на основе кодов Баркера // Труды учебных заведений связи. 2022. Т. 8, № 1. С. 8–14. https://doi. org/10.31854/1813-324X-2022-8-1-8-14.
6. Chu D. Polyphase codes with good periodic correlation properties (corresp.) // IEEE Transactions on information theory. 1972. Vol. 18, no. 4. P. 531–532.
7. Zhou Z., Helleseth T., Parampalli U. A family of polyphase sequences with asymptotically optimal correlation // IEEE Transactions on Information Theory. 2018. Vol. 64. no. 4. P. 2896–2900.
8. Сенин А. И. Корреляционные свойства последовательностей, построенных на основе М-последовательностей и последовательностей Уолша // Вестник Московского государственного технического университета им. Н. Э. Баумана. Серия «Приборостроение». 2014. № 5. С. 88–97.
9. Вакман Д. Е., Седлецкий Р. М. Вопросы синтеза радиолокационных сигналов. М. : Сов. радио, 1973. 312 с.
Об авторах
А. И. ДёмкоРоссия
кандидат технических наук, доцент, почетный работник высшего образования РФ
Е. Г. Алмазова
Россия
старший преподаватель
Рецензия
Для цитирования:
Дёмко А.И., Алмазова Е.Г. Оценка минимального достижимого уровня боковых лепестков функции неопределенности радиоимпульсных последовательностей. Вестник кибернетики. 2024;23(3):96-102. https://doi.org/10.35266/1999-7604-2024-3-11
For citation:
Dyomko A.I., Almazova E.G. Assessment of minimum achievable sidelobes level of ambiguity function for radio pulse sequences. Proceedings in Cybernetics. 2024;23(3):96-102. (In Russ.) https://doi.org/10.35266/1999-7604-2024-3-11















