Перейти к:
Анализ и сравнение блочных алгоритмов симметричного шифрования
https://doi.org/10.35266/1999-7604-2024-4-6
Аннотация
. В современном мире криптография стала неотъемлемой частью информационной безопасности. В условиях постоянного развития технологий и увеличения объемов, передаваемых данных, необходимость их надежной защиты становится крайне актуальной. Эта статья посвящена сравнительному анализу современных симметричных алгоритмов шифрования. Критериями сравнения были приняты безопасность, сложность, производительность, применимость, а также стандартизация.
Ключевые слова
Для цитирования:
Поддубный И.В., Брагинский М.Я. Анализ и сравнение блочных алгоритмов симметричного шифрования. Вестник кибернетики. 2024;23(4):60–68. https://doi.org/10.35266/1999-7604-2024-4-6
For citation:
Poddubnyy I.V., Braginsky M.Ya. Analysis and comparison of block symmetric encryption algorithms. Proceedings in Cybernetics. 2024;23(4):60–68. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-6
ВВЕДЕНИЕ
Сложно спорить с тем, что криптография играет одну из главных ролей в защите информации в цифровом мире. Вопросы, связанные с криптобезопасностью, стали особенно актуальны с появлением исследований квантовых вычислений. Симметричное шифрование является крайне распространенным за счет своих особенностей, связанных с высокой эффективностью, позволяющим не терять производительность даже при увеличении скорости обмена информацией.
Цель данного исследования заключается в сравнительном анализе алгоритмов симметричного шифрования блочного типа. Задачи исследования включают: оценку устойчивости алгоритмов к различным видам атак, анализ требований к ресурсам, производительности, а также оценку сложности реализации конкретных алгоритмов.
Невзирая на значительное количество исследований в этой теме, некоторые вопросы требуют дополнительного изучения. Например, вопросы, связанные с совместимостью алгоритмов шифрования с современными протоколами передачи данных, и их адаптация к новейшим угрозам безопасности. Нельзя также не обратить внимание на вопрос производительности алгоритмов в различных условиях их применения.
МАТЕРИАЛЫ И МЕТОДЫ
Существуют два основных типа симметричных алгоритмов: блочные и потоковые шифры. Блочный шифр оперирует блоками открытого и зашифрованного текстов, размер которых зачастую равен 64 бита. Потоковый шифр взаимодействует с открытым и зашифрованным текстом, обрабатывая по одному биту, байту или слову из 32 бит. Главной особенностью, отличающей один тип от другого, можно считать тот факт, что блочный шифр преобразует один и тот же блок открытого текста в один и тот же блок шифротекста, а потоковый шифр один и тот же символ при каждом шифровании превращает в разные символы шифротекста. В этой работе рассматриваются алгоритмы блочного типа.
Данное исследование касается трех блочных алгоритмов шифрования: Data Encryption Standard (далее – DES), FEAL (Fast data Encipherment Algorithm) и ГОСТ 28147-89. Эти алгоритмы были выбраны в связи с их широкой применяемостью и значимостью в области информационной безопасности.
Алгоритм DES, разработанный в 1975 г. и принятый как стандарт годом позже, представляет собой блочных шифр, оперирующий 64-битовыми блоками. То есть на вход алгоритму поступает открытый текст длинной 64 бита, а в результате работы алгоритма на выходе получится 64 бита зашифрованного текста. Длина ключа, используемого при шифровании, равняется 56 битам. Причем он представляется в виде 64-битовой числовой последовательности, но каждый восьмой бит является битом проверки на четность для проверки правильности ключа.
Алгоритм DES использует исключительно стандартную арифметику и логические операции над блоками, что позволяло легко реализовывать его даже на аппаратуре 1970-х годов. В нем применяются два основных метода шифрования: смещение и перестановка. Такая комбинация этих методов повторяется 16 раз, то есть выполняется 16 раундов. Причем для каждого нового раунда исходный 56-битный ключ используется для генерации новых наборов 48-битных подключей, используя специальную заданную последовательность перестановок.
Перед первой и после заключительной перестановок выполняется специальная перестановка, при которой входной блок переставляется по заданной последовательности перестановок. Важно отметить, что заключительная перестановка является обратной по отношению к начальной, что позволяет использовать один и тот же алгоритм как для шифрования, так и для расшифровки. Затем блоки разделяются на две 32-битовые последовательности: левую и правую. Затем выполняется 16 раундов. Затем происходят операции перестановки с расширением, операция XOR с ключом, подстановка с помощью S-блоков и прямая перестановка.
Расширяющая перестановка позволяет расширить правую половину данных с 32 бит до 48. Основной криптографической целью данной операции является усиление лавинного эффекта, из-за которого возрастает зависимость битов результата от битов исходных данных за счет влияния одного бита на две подстановки. То есть алгоритм DES спроектирован так, чтобы зависимость каждого бита шифротекста от каждого бита открытого текста и каждого бита ключа возникала как можно раньше.
Подстановка с помощью S-блоков представляет из себя восемь таблиц (эти таблицы являются константами и доступны во многих источниках, например [1]), состоящих из четырех строк и шестнадцати столбцов. Каждый элемент является 4-битовым числом. 48-битовое сообщение делится на каждый из восьми S-блоков и преобразуется по следующему правилу: из 6 бит на входе S-блока берется первый и шестой бит, они объединяются и образуют 2-битовое число, которое соответствует строке таблицы, а биты со второго по пятый образуют 4-битовое число, которое соответствует столбцу. Найденное 4-битовое число и является искомой подстановкой. Важно отметить, что подстановка с помощью S-блоков является ключевым этапом всего алгоритма DES, так как другие этапы алгоритма являются линейными и поддаются анализу. В свою очередь, описанные подстановки являются нелинейными, и именно они обеспечивают этому алгоритму криптостойкость. Затем прямая перестановка перетасовывает все биты сообщения по специальному P-блоку (так же, как и S-блок он является константой [1]). При этом никакие биты не теряются и не используются дважды. С точки зрения затрат памяти DES позволяет использовать крайне малое ее количество. Это связано с длинной ключа 56 битов и оперируемым 64-битовым блоком данных.
К сожалению, алгоритм шифрования DES с 2012 г. является крайне нерекомендованным к использованию [2]. Причем в научных кругах его критиковали практически с самого его появления [3]. Основными темами для обсуждения стали длина ключа, множество констант в виде S-блоков и количество итераций самого алгоритма.
Длина ключа является крайне важным аспектом любого алгоритма шифрования. Это связано с возможностью его получения методом грубой силы – обычным перебором всех возможных значений ключа. В момент разработки алгоритма было понимание того, что лишь суперкомпьютер за 20 млн долл. сможет раскрыть ключ за один день, однако уже к 1990 г. стало очевидно, что стандарт DES в течение нескольких лет полностью утратит свою криптостойкость.
Вопросы, касающиеся S-блоков, связаны с озабоченностью, что во время их разработки государственные структуры США оставили намеренные лазейки, позволяющие без труда осуществлять криптоанализ алгоритма. Также в научных источниках можно найти различные замечания об особенностях составления S-блоков, но использовать их для атак на алгоритм так и не получилось [4].
Вопросы, связанные с количеством раундов, обращаются к выбору именно 16 раундов. Описанный выше лавинный эффект возникает после 8 раундов [5]. Причем при попытке применить в алгоритме менее 16 раундов, он начинает быть уязвим к атаке с известным открытым текстом.
Алгоритм FEAL был впервые опубликован в 1987 г. В нем используется 64-битовый блок и 64-битовый ключ. Он является идейным преемником рассмотренного выше алгоритма DES, но с усовершенствованной функцией раунда и попыткой увеличения скорости шифрования за счет уменьшения количества раундов.
Шифрование в алгоритме начинается с операции XOR над правой половиной, полученной в результате разделения исходной последовательности на две 32-битовые последовательности. Затем они проходят через n раундов (важно отметить, что в первой редакции алгоритм насчитывал лишь 4 раунда), на каждом из которых правая половина комбинируется с 16 битами ключа действиями, описанными ниже, и суммируется операцией XOR с левой половиной. Затем половины переставляются. После n раундов начинается этап, при котором половины не переставляются. Левая и правая половины суммируются операцией XOR и сцепляются в один 64-битовый блок. Затем операцией XOR он суммируется с другими 64 битами ключа, и на этом алгоритм заканчивается. Полный алгоритм проиллюстрирован на рис. 1 [6].
Комбинирование в алгоритме FEAL заключается в преобразовании 32 бит данных и 16 бит ключа при помощи разделения данных на 8-битовые фрагменты, суммирования операцией XOR и заменой друг друга. Внутри этой функции используется две функции, которые определены следующим образом.
В алгоритме FEAL используется функция генерации ключа, которая заключается в делении на две половины 64-битового ключа, а затем применение к ним операции XOR и функции ƒ, изображенной на рис. 2. В ней происходит разбиение двух 32-битовых последовательностей на 8-битовые блоки, которые комбинируются и заменяются. Функции ƒk для вычисления и проиллюстрированы на рис. 3. Полученные 16-битовые блоки ключа используются в основном алгоритме. Важно отметить, что алгоритм FEAL имеет крайне низкие требования к памяти благодаря небольшой длине ключа и малому количеству раундов.
Криптоанализ алгоритма уже в 1989 г. показал, что для атаки на алгоритм FEAL достаточно подобрать открытый текст размером 10000 блоков [7]. Эта научная работа спровоцировала появление усовершенствованного алгоритма FEAL-N, особенность которого заключается в переменном числе раундов, а впоследствии и FEAL-NX, который использовал 128-битовый ключ. Алгоритм этого шифра показан на рис. 4. Со временем в алгоритм привнесли динамическую функцию перестановки и назвали его FEAL-N (X)S.
Симметричный блочный криптоалгоритм ГОСТ 28147-89 был разработан в Советском Союзе в 1989 г. Этот алгоритм является 64-битовым, длина ключа шифра составляет 256 бит. Алгоритм состоит из 32 раундов, в каждом из которых применяется довольно тривиальный алгоритм шифрования. Как и в рассмотренных выше алгоритмах, открытый текст длиной 64 бита делится на две 32-битовые половины и для каждого i-го раунда выполняются две операции, используя подключ K_i:
L_i = R_(i-1); R_i=L_(i-1) ⨁ f(R_(i-1),K_i).
Одна из основных особенностей алгоритма ГОСТ заключается в использовании в шифровании секретных S-блоков, которые так же, как и ключ, должны храниться в тайне. Правая половина и i-й подключ суммируются по модулю. Затем полученная строка делится на восемь 4-битовых последовательностей, каждый из которых проходит через один из S-блоков. В качестве подключей используется исходный ключ, раздробленный на восемь 32-битовых последовательностей. Причем в каждом раунде применяется своя ключевая последовательность, просто меняя их поочередно.
В криптоанализе ГОСТ научные исследователи делают акцент на сложности проведения атаки методом грубой силы. Это связано с большой по тем временам ключевой последовательностью – 256 бит. Учитывая закон Мура, такой алгоритм в теории сможет оставаться безопасным по крайней мере 200 лет. Также нужно понимать, что секретность S-блоков и большое количество раундов, в сравнении с вышеописанным DES, повышает сложность алгоритма для атакующего еще и с позиции дифференциального и линейного криптоанализа. Стоит учитывать, что благодаря большой длине ключа и 64-битовой шифруемой последовательности ГОСТ требует для работы больше памяти, чем алгоритмы FEAL и DES.
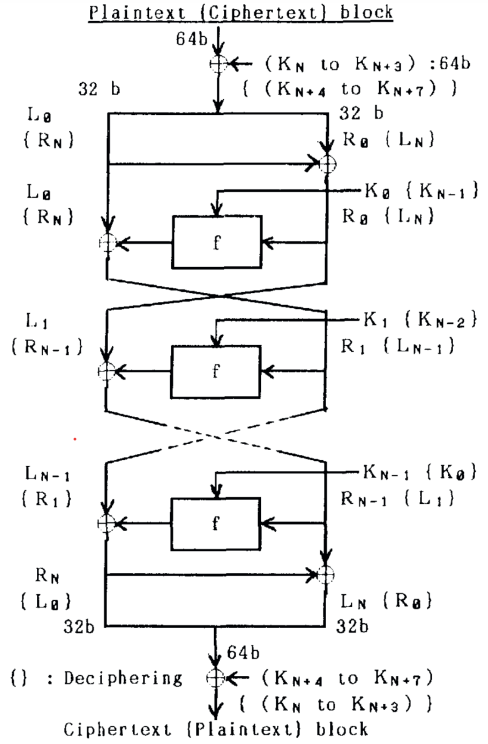
Рис. 1. Один раунд алгоритма FEAL
Примечание: взято из [6].
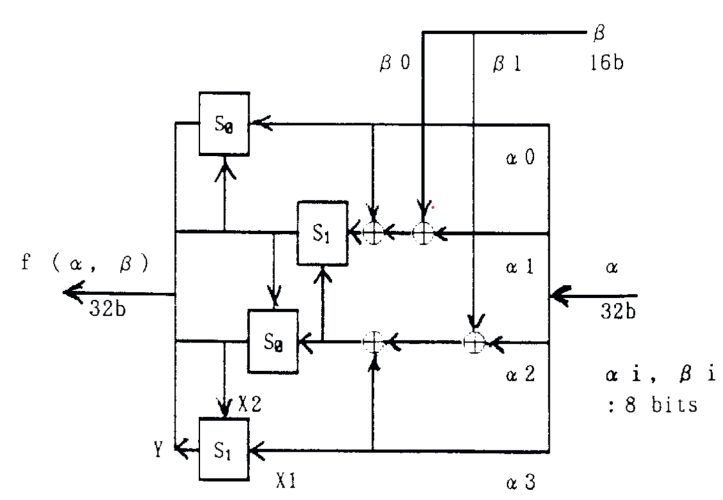
Рис. 2. Функция ƒ
Примечание: взято из [6].
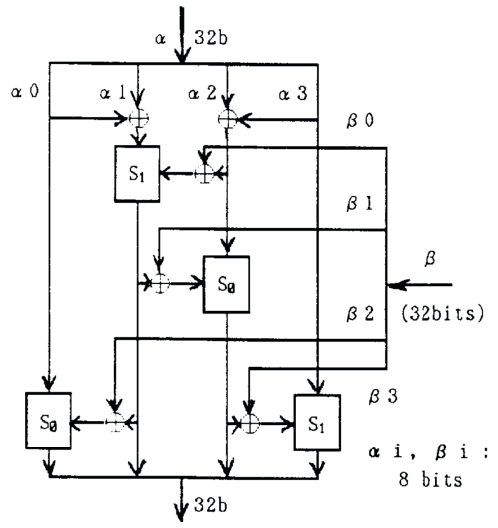
Рис. 3. Функция ƒk
Примечание: взято из [6].
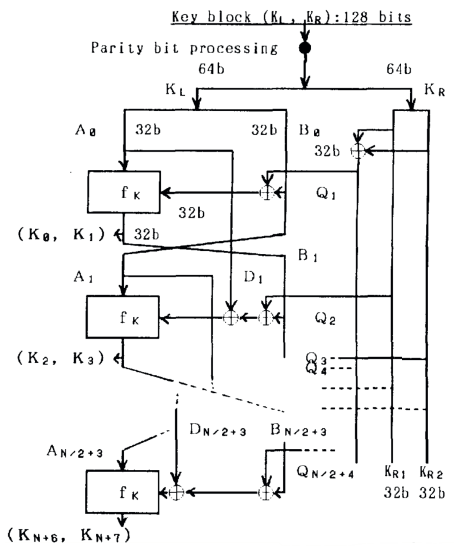
Рис. 4. Алгоритм FEAL-NX
Примечание: взято из [6].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Цель исследования заключалась в сравнительном анализе алгоритмов симметричного шифрования блочного типа. Основная гипотеза работы заключалась в том, что, несмотря на схожесть в принципах работы, описанные алгоритмы имеют значительные различия в уровне защиты и эффективности.
С точки зрения устойчивости к атакам про каждый алгоритм можно сказать следующее.
- Алгоритм ГОСТ применяется в России и ряде других стран по сей день. Его основными достоинствами являются длина ключа 256 битов, 32 раунда шифрования, а также секретные S-блоки. Это позволяет быть устойчивым на протяжении десятилетий к атаке методом грубой силы и дифференциальному криптоанализу, хотя и с некоторыми оговорками [8].
- FEAL – это алгоритм шифрования, который способен работать с ключами более 128 битов и использует сложные методы замен и подстановок, за счет чего он устойчив не только к атаке методом грубой силы, но еще и к дифференциальному криптоанализу.
- DES использует всего 56 битов ключевых данных, что делает его крайне ненадежным к атаке методом грубой силы, а за счет малого количества раундов позволяет реализовывать атаки с использованием открытых текстов и дифференциального анализа.
Для сравнения с практической точки зрения эффективности описанных алгоритмов были написаны программы на языке Си для оценки временных затрат на шифрование и дешифрование. В качестве исходных кодов применялись реализации алгоритм ГОСТ [9], алгоритм DES [10] и алгоритм FEAL [11]. В одном тесте выполнялись шифровка и дешифровка, используя в качестве входной и ключевой последовательности выходную последовательность предыдущего теста. Для первого теста открытый текст и ключевая последовательность представляет собой шестнадцатеричное число 9474B8E8C73BCA7D. Таким образом, в каждом тесте ни ключевая последовательность, ни открытый текст не повторялись дважды. Время, требуемое на эти операции, отсчитывалось программным методом. Всего для каждого алгоритма было проведено 1000 тестов, чтобы минимизировать влияние других процессов системы на итоговый результат. Тесты выполнялись подряд без изменения аппаратной и программной конфигурации тестового стенда. Итоговые графики представлены на рис. 5–7, при изучении которых можно обнаружить некоторые временные «всплески». Это связано с работой фоновых процессов в операционной системе тестового стенда.
Также были вычислены средние времена решения задач шифрования и дешифрования для каждого рассмотренного алгоритма шифрования (табл. 1).
По представленным результатам можно сделать следующие выводы.
- Алгоритм FEAL показал наилучший результат среди рассмотренных алгоритмов по времени шифрования и дешифрования. Среднее время выполнения 1000 итераций алгоритма составило около 959 мс. Это подтверждает его сравнительно высокую эффективность и делает его наиболее предпочтительным выбором для алгоритмов, требующих высокую скорость обработки данных.
- Тестирование алгоритма ГОСТ показало, что его эффективность лишь немного проигрывает алгоритму FEAL. Среднее время выполнения 1000 итераций составило около 1817 мс, что в 1,9 раза медленнее, чем алгоритм FEAL.
- DES при тестировании показал наихудшие результаты со средним результатом выполнения 1000 итераций около 8393 мс, что в 8,8 раза медленнее алгоритма FEAL. Этот результат подтверждает неактуальность этого алгоритма с точки зрения производительности и делает его непригодным в использовании в современных системах.
В заключение хочется подчеркнуть важную мысль о том, что алгоритм DES не только небезопасен с точки зрения криптоанализа, но еще и неэффективен в сравнении с аналогичными алгоритмами шифрования FEAL и ГОСТ. FEAL, в свою очередь, является эффективным для решения современных задач криптографии, а ГОСТ, занимая промежуточное положение, может быть использован для более специфичных задач, требующих алгоритмов российского производства.
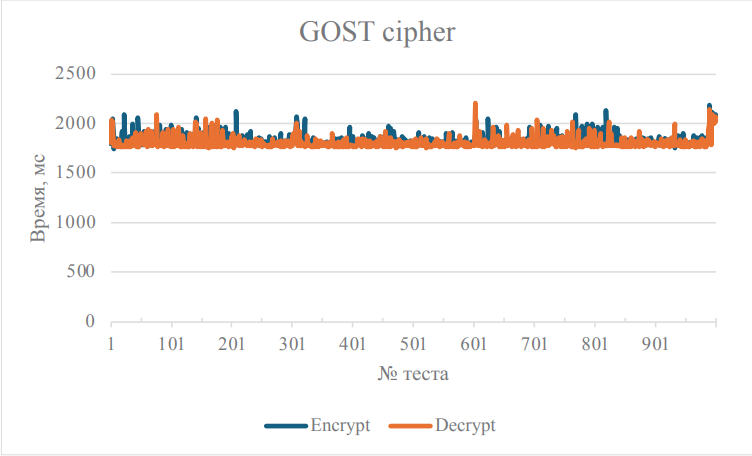
Рис. 5. График временных затрат на шифрование и дешифрование алгоритмом ГОСТ
Примечание: составлено авторами.
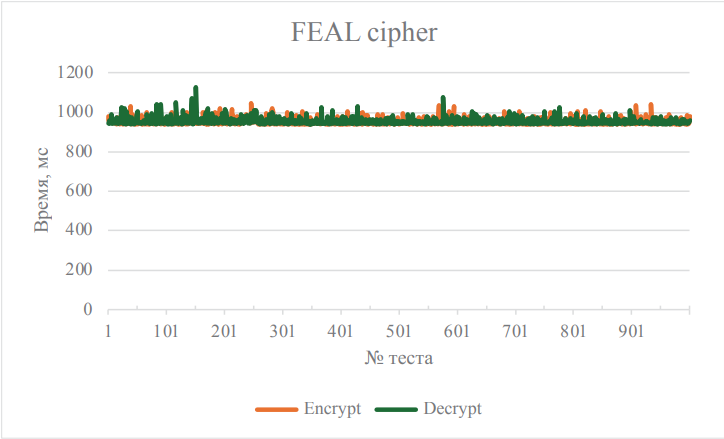
Рис. 6. График временных затрат на шифрование и дешифрование алгоритмом FEAL
Примечание: составлено авторами.

Рис. 7. График временных затрат на шифрование и дешифрование алгоритмом DES
Примечание: составлено авторами.
Таблица 1
Результаты тестирования алгоритмов шифрования
|
Название алгоритма |
Среднее время шифрования 1000 открытых текстов, мс |
Среднее время дешифрования 1000 открытых текстов, мс |
Среднее время шифрования и дешифрования 1000 открытых текстов, мс |
Отношение к наилучшему результату по среднему времени шифрования и дешифрования |
|
ГОСТ |
1825,892 |
1808,496 |
1817,194 |
1,9 |
|
FEAL |
958,322 |
959,303 |
958,8125 |
1 |
|
DES |
8399,292 |
8387,661 |
8393,4765 |
8,8 |
Примечание: составлено авторами.
ЗАКЛЮЧЕНИЕ
В рамках описанной работы были озвучены цели и задачи, направленные на оценку алгоритмов симметричного шифрования блочного типа с точки зрения их эффективности, требований к ресурсам, а также защищенности. В процессе исследования получилось подтвердить мысль о том, что, несмотря на сравнительно похожие алгоритмы, используемые в каждом из шифров, итоги анализа и тестов сильно различаются.
Алгоритм DES в ходе анализа показал свою крайне слабую защиту к криптоанализу, и он по праву является не рекомендованным к использованию. Алгоритмы ГОСТ и FEAL являются вполне актуальными и по сей день, обеспечивая надежную защиту шифруемой информации.
Анализ требований к ресурсам показал, что алгоритм FEAL требует наименьшее количество вычислительных ресурсов, что позволяет его использовать, например, в различных мобильных системах.
Тестирование производительности показало, что FEAL является наиболее эффективным алгоритмом, обеспечивая минимальные временные затраты на шифрование и дешифрование. Алгоритм ГОСТ продемонстрировал временные затраты на те же операции чуть выше, однако в разы лучше, чем алгоритм DES.
В заключение этого исследования стоит еще раз подчеркнуть важность выбора алгоритма в зависимости от конкретных требований к безопасности и производительности. Анализируя вектор развития технологий, можно полагать, что с ростом вычислительных мощностей будут появляться новые, более совершенные алгоритмы шифрования, которые будут обеспечивать высокий уровень защиты и эффективности. Важно понимать, что растущее количество кибератак делает более актуальными вопросы, связанные с кибербезопасностью, что ведет к необходимости проведения дальнейших исследований в этой области и усовершенствования существующих алгоритмов шифрования для поддержания их актуальности в вопросах, связанных с ответом на новые вызовы в области информационной безопасности.
Список литературы
1. The DES Algorithm Illustrated. URL: https://page.math.tu-berlin.de/~kant/teaching/hess/krypto-ws2006/des.htm (дата обращения: 27.09.2024).
2. Remove the highly insecure DES encryption from the User accounts. URL: https://learn.microsoft.com/en-us/services-hub/unified/health/remediation-steps-ad/remove-the-highly-insecure-des-encryption-from-user-accounts (дата обращения: 27.09.2024).
3. Denning D. E., Dorothy E. Digital signatures with RSA and other public-key cryptosystems. Communications of the ACM. USA : ACM, 1984. p. 388–392.
4. Davio M., Desmedt Y., Fosseprez M. et al. Analytical Characteristics of the DES. Advances in Cryptology. Heidelberg : Springer, 1984. p. 171–202.
5. Konheim A. G. Cryptography, a primer. New York, 1981. 432 p.
6. Miyaguchi S. The FEAL Cipher Family. Advances in Cryptology-CRYPTO’ 90. Heidelberg : Springer, 1990. p. 628–638.
7. Gilbert H., Chasse G. A Statistical Attack of the FEAL-8 Cryptosystem. Advances in Cryptology. Heidelberg : Springer, 1991. p. 22–33.
8. Ko Y., Hong S., Lee W. et al. Related Key Differen- tial Attacks on 27 Rounds of XTEA and Full-Round GOST. Heidelberg : Springer, 2004. P. 299–316.
9. Шнайер Б. Прикладная криптография: протоколы, алгоритмы и исходный код на С. 2-е изд. М. : Диалектика, 2022. 1040 с.
10. DES algorithm. URL: https://github.com/dhuertas/DES/blob/master/des.c (дата обращения: 01.10.2024).
11. feal-8.c. URL: https://github.com/deeptechlabs/encryption/blob/master/FEAL8-WI/feal-8.c (дата обращения: 01.10.2024).
Об авторах
И. В. ПоддубныйРоссия
магистрант
М. Я. Брагинский
Россия
кандидат технических наук, доцент
Рецензия
Для цитирования:
Поддубный И.В., Брагинский М.Я. Анализ и сравнение блочных алгоритмов симметричного шифрования. Вестник кибернетики. 2024;23(4):60–68. https://doi.org/10.35266/1999-7604-2024-4-6
For citation:
Poddubnyy I.V., Braginsky M.Ya. Analysis and comparison of block symmetric encryption algorithms. Proceedings in Cybernetics. 2024;23(4):60–68. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-6















