Перейти к:
О математических моделях размещения оборудования при проектировании и реконструкции предприятий
https://doi.org/10.35266/1999-7604-2024-4-9
Аннотация
Приводится обзор математических моделей размещения технологического оборудования, применяемых при решении задач проектирования и модернизации производственных цехов. Рассматриваются случаи размещения взаимосвязанного оборудования. Построена математическая модель размещения производственных линий и технологического оборудования на них. Линии соединены вертикальным виадуком, через который проводятся коммуникации. На линиях зафиксированы запрещенные зоны, где нельзя располагать другие элементы. Приведены результаты численных экспериментов с применением построенной модели нелинейного программирования и пакета CPLEX. Рассмотрены две серии тестовых примеров, когда расположение виадука фиксировалось и когда находилось его оптимальное размещение. При поиске расположения виадука получилось лучшее значение целевой функции, чем при фиксированном виадуке, но время счета увеличивалось. Модель может быть использована при проектировании и оценке размещения технологических линий с оборудованием в промышленных отраслях.
Для цитирования:
Веремчук Н.С. О математических моделях размещения оборудования при проектировании и реконструкции предприятий. Вестник кибернетики. 2024;23(4):92-99. https://doi.org/10.35266/1999-7604-2024-4-9
For citation:
Veremchuk N.S. On mathematical models of equipment placement in design and reconstruction of enterprises. Proceedings in Cybernetics. 2024;23(4):92-99. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-9
Введение
В последние годы при разработке проектных решений предприятий широко применяются математическое моделирование и методы оптимизации [1, 2]. Большое значение при этом отводится решению задач оптимального размещения технологических линий, оборудования [3, 4]. Острая необходимость в решении таких задач возникает на этапах проектирования и реконструкции производственных участков. Неоптимальное размещение может привести к серьезным затратам не только финансовым, но и ресурсным. При выполнении проектирования сначала, как правило, определяется расположение технологических линий и далее осуществляется оптимальное размещение оборудования на них. В некоторых случаях положение линий находится с учетом уже фиксированного расположения оборудования. Все это определяется спецификой предприятия и его производственной деятельностью. При реконструкции предприятий положение производственных линий фиксировано и требуется заменить некоторые единицы оборудования с целью переналадки производства, например, на выпуск новой продукции. В таких случаях часть оборудования остается на месте. Его можно рассматривать как специальные области (запрещенные зоны), где невозможно новое расположение объектов [5, 6].
Технологическое оборудование может быть связано между собой и с внешними объектами различными коммуникациями (связями). Причем могут варьироваться и способы прокладки коммуникаций, например, через специальные проходы между линиями (виадуками). При этом часто необходимо минимизировать суммарную стоимость коммуникаций. Кроме того, активное внимание уделяется вопросам минимизации занимаемой оборудованием площади. Такие задачи широко применяются в условиях ограниченности занимаемых площадей производственных цехов [4][7]. С целью сокращения суммарных затрат, связанных с размещением оборудования, следует уделять внимание проектированию и оптимальному расположению технологических линий производства в процессах проектирования, реконструкции предприятий.
В данной работе приводится обзор математических моделей размещения технологического оборудования при проектировании и реконструкции производственных цехов. Построена модель нелинейного программирования для задачи размещения линий с технологическим оборудованием. Соседние линии соединены вертикальным виадуком, через который проводятся коммуникации. На линиях имеются фиксированные прямоугольные запрещенные зоны, размещение в которых не допускается. Приведены результаты численных экспериментов с применением построенной модели нелинейного программирования и пакета CPLEX. Рассмотрены две серии тестовых примеров: первая – при фиксированном расположении виадука; вторая – когда оптимальное расположение виадука находилось в результате решения задачи. Полученные результаты могут быть полезны при проектировании и реконструкции производственных цехов.
Материалы и методы
- Математическая модель размещения единиц швейного оборудования
В работе [8] построена математическая модель размещения модулей швейного оборудования. Технологическое оборудование комплектуется в специализированные модули для обработки деталей.
При производстве одного вида изделия применяются разные виды модулей. Это диктуется технологической картой производства продукции. Модуль – это прямоугольник длины li и ширины hi (рис. 1).
С учетом направления швейного потока в цехе размещение модулей осуществляется вдоль осевых линий. Требуется разместить модули на линиях так, чтобы минимизировать площадь под оборудованием (рис. 1).
Пусть m – число линий, а n – количество модулей. Переменная xik принимает значение 1, если модуль с номером i находится на линии с номером k, и 0 – иначе.
xik {0,1}, i = 1, ..., m; k = 1, ..., m.(1)
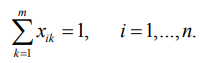 (2)
(2)
Дополнительные ограничения на размещение модулей можно записать так:
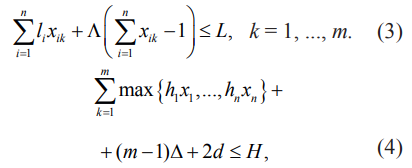
где L и H – длина и ширина производственного участка, Λ – минимально допустимые расстояния между модулями, Δ – минимальное расстояние между оборудованием на соседних линиях, d – минимальное допустимое расстояние.
Максимальная суммарная длина модулей на линиях определяется выражением:
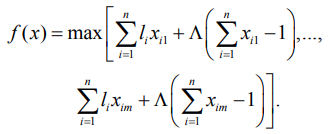 (5)
(5)
Ширина окаймляющего прямоугольника g(x*), содержащего все оборудование, для некоторого набора булевых переменных x* = (x*ik), i = 1, ..., n, k = 1, ..., m, определяется выражением:
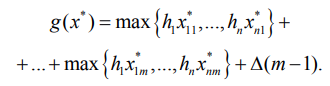
Соотношения между сторонами окаймляющего прямоугольника можно записать в виде:
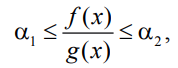 (6)
(6)
где α1 и α2 – параметры.
В результате решения требуется минимизировать площадь окаймляющего прямоугольника:
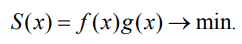 (7)
(7)
Для решения задачи (1)–(7) предложены алгоритмы последовательно-одиночного размещения [8].
- Модель многокритериальной оптимизации
В процессе конструкторско-технологической подготовки производства часто требуется решать многокритериальные оптимизационные задачи, например для предприятий промышленности [9]. При этом возникает необходимость рассматривать решение задач размещения технологического оборудования.
Пусть J = {1, ..., n} – множество номеров размещаемых объектов с длиной и шириной , M = {1, ..., m} – множество номеров осевых линий, переменная если объект j расположен на линии k, иначе ј Ј, k M.
Модель целочисленного программирования имеет вид [10]:
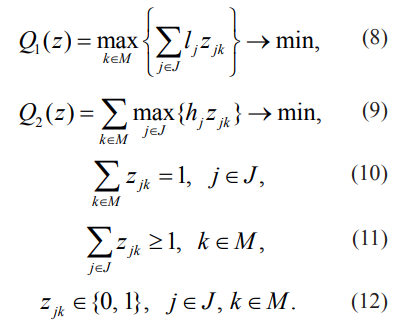
Рассматриваются два критерия – минимизация максимальной суммарной длины объектов на линиях (8) и минимизация суммарной ширины максимальных по ширине объектов на каждой линии (9). Условия расположения объектов на линиях заданы в ограничениях (10) и (11).
В работе [10] для поиска оптимального решения задачи (8)–(12) применялся метод уступок и решалась серия однокритериальных задач.
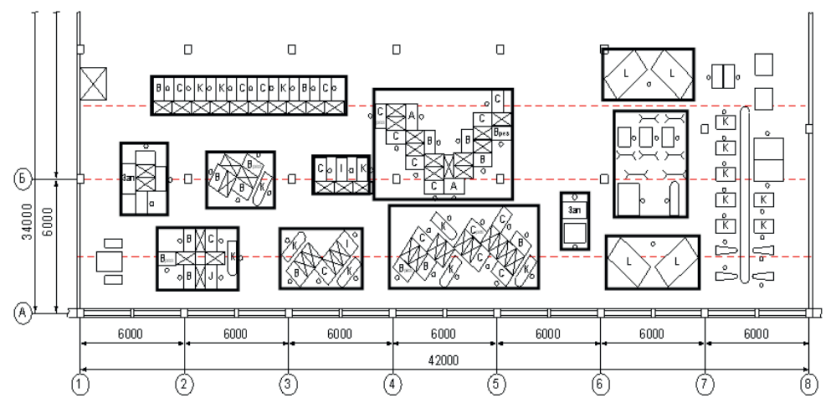
Рис. 1. Пример расположения технологических линий
Примечание: скриншот автора.
Таблица 1
Решение задач при фиксированном виадуке
|
№ |
n |
m |
hmax |
x0 |
G |
t |
|
1 |
3 |
4 |
4 |
9 |
960 |
0,17 |
|
2 |
3 |
4 |
7 |
9 |
1137 |
0,10 |
|
3 |
5 |
5 |
4 |
22 |
3211 |
0,14 |
|
4 |
5 |
5 |
15 |
22 |
4333 |
0,15 |
|
5 |
10 |
4 |
4 |
21 |
7455 |
114 |
|
6 |
10 |
4 |
10 |
21 |
8583 |
116 |
|
7 |
12 |
5 |
7 |
7 |
8726 |
246 |
|
8 |
12 |
5 |
10 |
12 |
9695 |
419 |
|
9 |
15 |
10 |
8 |
10 |
21794 |
34 |
|
10 |
15 |
10 |
15 |
20 |
27254 |
70 |
|
11 |
17 |
12 |
18 |
21 |
33005,5 |
149 |
|
12 |
17 |
12 |
25 |
30 |
42806,5 |
65 |
|
13 |
20 |
15 |
12 |
14 |
33437 |
125 |
|
14 |
20 |
15 |
15 |
21 |
39661 |
132 |
|
15 |
25 |
20 |
8 |
10 |
70455 |
112 |
|
16 |
25 |
20 |
10 |
14 |
75039 |
173 |
Примечание: составлено авторами.
Таблица 2
Решение задач при нефиксированном виадуке
|
№ |
n |
m |
hmax |
x0 |
G |
t |
|
1 |
3 |
4 |
4 |
6 |
802 |
0,19 |
|
2 |
3 |
4 |
7 |
6 |
979 |
0,12 |
|
3 |
5 |
5 |
4 |
11 |
2093 |
0,17 |
|
4 |
5 |
5 |
15 |
11 |
3215 |
0,20 |
|
5 |
10 |
4 |
4 |
9 |
5166 |
162 |
|
6 |
10 |
4 |
10 |
9 |
6294 |
188 |
|
7 |
12 |
5 |
7 |
9 |
8630 |
612 |
|
8 |
12 |
5 |
9 |
12 |
9675 |
1219 |
|
9 |
15 |
10 |
13 |
10 |
21149 |
149 |
|
10 |
15 |
10 |
13 |
20 |
27159 |
152 |
|
11 |
17 |
12 |
14 |
21 |
32188,5 |
362 |
|
12 |
17 |
12 |
14 |
30 |
38362,5 |
230 |
|
13 |
20 |
15 |
14 |
14 |
33270 |
773 |
|
14 |
20 |
15 |
14 |
21 |
39563 |
572 |
|
15 |
25 |
20 |
16 |
10 |
65073 |
786 |
|
16 |
25 |
20 |
16 |
14 |
71881 |
933 |
Примечание: составлено авторами.
Результаты и их обсуждение
Модель размещения взаимосвязанных объектов
Рассмотрим случай размещения взаимосвязанных объектов на линиях. Пусть положение линий неизвестно и его требуется найти. Для удобства рассмотрим случай двух линий.
Заданы два параллельных отрезка длиной LS с фиксированными на них прямоугольниками – запрещенными зонами. Расположение новых элементов в запрещенных зонах недопустимо. Отрезки будем далее называть линиями. С целью возможности обслуживания оборудования линии должны быть на таком расстоянии друг от друга, чтобы между ними выполнялись прямые проезды.
Задано множество новых прямоугольных объектов (оборудование), центры которых связаны коммуникациями между собой и с зонами. Коммуникации между объектами и зонами на разных линиях должны проходить через вертикальную составляющую (виадук).
Задача состоит в нахождении оптимального размещения линий и новых объектов на них вне запрещенных зон так, чтобы суммарная стоимость коммуникаций объектов между собой и с зонами, а также площадь, занимаемая линиями с оборудованием, были минимальны.
Пусть Xi и Fj – это объекты и зоны с длиной и высотой li , hxi и pi, hfi, и центрами (xi, yi) и (b1i, b2i), где i I = {1, ..., n} и Обозначим через wij ≥ 0, uik ≥ 0 стоимость связей между Xi и Fj, Xi и Xk для i, ј Ј, i < k, соответственно. Пусть линии параллельны оси Ох и левая граница каждой из них находится в точке (0, Lyt), где t = 1,2, Ly1 ≤ Ly2, δ – расстояние между линиями. Положение линий определяется в ходе решения задачи, поэтому значения Lyt неизвестны.
Представим множество J в виде объединения 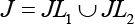 , где Lyt – множество номеров зон на линии с номером t, t = 1,2.
, где Lyt – множество номеров зон на линии с номером t, t = 1,2.
Вертикальный виадук, соединяющий линии, обозначим через V, а абсциссу точки его расположения – через x0. Отметим, что высота виадука V будет равна Ly2 – Ly1.
Задача заключается в поиске расположения линий и объектов X1, ..., Xn на них вне запрещенных зон F1, ..., Fm так, чтобы они не пересекались друг с другом и суммарная стоимость связей объектов между собой и с зонами, а также площадь окаймляющего прямоугольника S = LS • Ly2 были минимальны.
С учетом вышесказанного условия минимизации площади S будут соответствовать условиям минимизации величины Ly2.
Введем булевы переменные: zit = 1, если Xi размещается на линии с номером t, i I, t = 1,2, и zit = 0 иначе.
Математическая модель для нефиксированных линий с виадуком и запрещенными зонами записывается так:
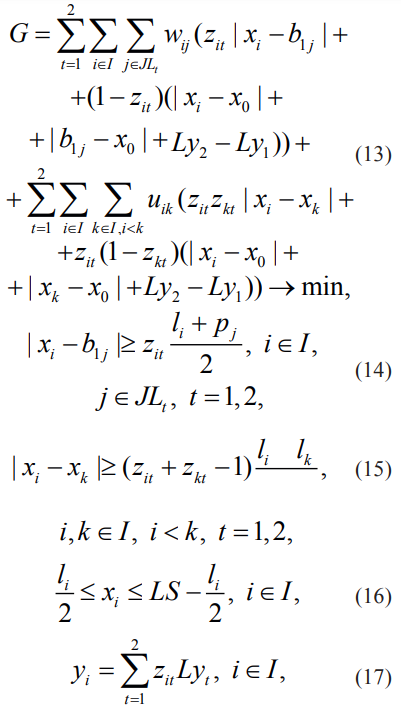
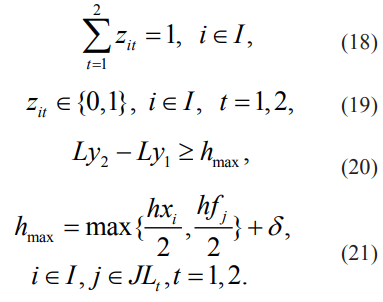
Построенная модель (13)– (21) может быть решена, например, с помощью решателя BARON.
Для случая фиксированных линий (Ly1, Ly2, x0 известны) модель (13)–(19) рассматривалась в работах [11, 12].
Результаты экспериментов с моделью размещения взаимосвязанных объектов
Отметим, что модель (13)–(21) нелинейна. Для нахождения локального оптимума задачи проведены две серии тестовых экспериментов с применением модели (13)–(21) и пакета CPLEX. Первая серия связана с поиском расположения производственных линий и объектов на них с фиксированным виадуком между линиями. Во второй серии находилось не только расположение линий и объектов на них, но также и оптимальное размещение виадука. Результаты экспериментов для каждой серии тестовых задач представлены в табл. 1 и 2, где t – это время счета в секундах в пакете CPLEX.
По результатам экспериментов можно отметить, что при поиске расположения виадука получено лучшее значение целевой функции, чем при фиксированном виадуке, но время счета увеличивалось.
- Модели, применяемые при модернизации цехов
При фиксированном расположении линий математическая модель (13)–(19) размещения технологического оборудования применяется при реконструкции и модернизации производственных предприятий на этапе проектирования. Для ее решения доказаны свойства, позволяющие декомпозировать задачу и рассматривать ее как дискретную, разработаны алгоритмы точного и приближенного решений [11, 12].
Заключение
Математические модели размещения технологического оборудования широко применяются при решении задач проектирования и модернизации производственных цехов. На этапах проектирования, как правило, положение линий с оборудованием определяется, на этапах модернизации – фиксировано. Часто при реконструкции цехов часть оборудования остается на месте, этот случай в приведенных моделях учитывается в качестве наличия запрещенных зон.
Построена модель нелинейного программирования для размещения линий и оборудования на них с учетом запрещенных зон. Приведены результаты численных экспериментов с применением построенной модели и пакета CPLEX. Рассмотрены две серии тестовых примеров. При поиске расположения виадука получилось лучшее значение целевой функции, чем при фиксированном виадуке, но время счета увеличивалось.
Область применения поставленной задачи – сфера машиностроения, проектирование технологических цехов, модернизация и переналадка имеющегося производственного оборудования.
Список литературы
1. Yue L., Guan Z., He C. et al. Slotting optimization of automated storage and retrieval system (AS/RS) for efficient delivery of parts in an assembly shop using genetic algorithm: A case Study // IOP Conference Series: Materials Science and Engineering. 2017. Vol. 215, no. 1. P. 012002.
2. Osinuga I. A., Bolarinwa A. A., Kazakovtsev L. A. A modified particle swarm optimization algorithm for location problem // IOP Conference Series: Materials Science and Engineering. 2019. Vol. 537, no. 4. P. 042060.
3. Dziki K., Krenczyk D. Mixed-model assembly line balancing problem with tasks assignment // IOP Conference Series: Materials Science and Engineering. 2019. Vol. 591, no. 1. P. 012013.
4. Sosedko V. V., Yanishevskaya A. G. Methods and means of determining the optimal location of industrial enterprises // IOP Conference Series: Journal of Physics: Conference Series. 2019. Vol. 1210, no. 1. P. 012136.
5. Prakash M. A., Raju K., Raju V. R. Facility location problems in the presence of two elliptical forbidden regions // Materials Today: Proceedings. 2018. Vol. 5, no. 2. P. 4000–4007.
6. Prakash M. A., Raju K., Raju V. R. Facility location in the presence of mixed forbidden regions // Interna- tional Journal of Applied Engineering Research. 2018. Vol. 13, no. 1, P. 91–97.
7. Akash P. L., Abyson S., Babu G. A firefly algorithm approach for multirow facility layout problem // IOP Conference Series: Materials Science and Engineering. 2018. Vol. 396, no. 1. P. 012072.
8. Легких С. А., Забудский Г. Г., Нагорная З. Е. Автоматизация проектирования планов производственных участков и цехов швейных предприятий // Естественные и технические науки. 2005. № 4. С. 261–266.
9. Chen R., Lu J., Zhang H. et al. Research on scheduling problem of discrete manufacturing workshop for major equipment in complicated environment // IOP Conference Series: Materials Science and Engineering. 2019. Vol. 688, no. 5. P. 055048.
10. Zabudskii G. G., Amzin I. V. Algorithms of compact location for technological equipment on parallel lines // Sibirskii Zhurnal Industrial’noi Matematiki. 2013. Vol. 16, no. 3. P. 86–94.
11. Zabudsky G. G., Veremchuk N. S. Numerical research of placement problem on lines with forbidden zones and routing communications // Journal of Physics: Conference Series. 2021. Vol. 1791, no. 1. P. 012089.
12. Zabudsky G. G., Veremchuk N. S. Optimization of the location of interconnected facilities on parallel lines with forbidden zones // Journal of Applied and Industrial Mathematics. 2021. Vol. 15, no. 4. P. 716–727.
Об авторе
Н. С. ВеремчукРоссия
кандидат физико-математических наук, доцент
Рецензия
Для цитирования:
Веремчук Н.С. О математических моделях размещения оборудования при проектировании и реконструкции предприятий. Вестник кибернетики. 2024;23(4):92-99. https://doi.org/10.35266/1999-7604-2024-4-9
For citation:
Veremchuk N.S. On mathematical models of equipment placement in design and reconstruction of enterprises. Proceedings in Cybernetics. 2024;23(4):92-99. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-9















