Перейти к:
Метод выбора управляющего решения при диапазонных входных сигналах для детерминированно-стохастической модели
https://doi.org/10.35266/1999-7604-2024-4-11
Аннотация
В статье рассмотрена область применения алгоритмов управления многокомпонентной динамической системой с неопределенными параметрами, меняющимися в зависимости от нестабильного диапазонного потока входных данных. Предложенная методика направлена на упрощение процесса анализа и отбора диапазонов данных с различным уровнем актуальности, используемых для формирования управляющего воздействия. Представлена математическая модель, описывающая соотношения между запасами данных и потоками, что позволяет выявить ключевые параметры системы и сосредоточиться на их дальнейшей детализации. Допущение о переходе данных между классами основывается на автоматической актуализации данных, что отражает реальные условия эксплуатации системы. Изначально классы данных не имеют строгой иерархии, однако их объем изменяется в зависимости от временных интервалов, причем наиболее значительные изменения происходят ближе к концу исследуемого периода. Эти изменения обусловлены внутренними перемещениями данных между классами и внешними потоками данных. Ожидаемый поток данных рассчитывается на основе начального запаса и вероятности перехода, что согласуется с предположением о пропорциональности потоков запасам. Общее число новых данных равно числу выбывающих данных.
В результате сравнения стандартных технологий алгоритмизации и кодирования с предлагаемым методом и последующей оценки выявлено повышение производительности системы, а также предсказуемость критических состояний, которые могут возникнуть в любой момент при наличии неопределенных параметров. Реализована программная модель считывания и интерпретации входных сигналов, идентификации и корректировки артефактов, обработки входных данных, тестирования многокомпонентной динамической системы с диапазонными входными данными.
Ключевые слова
Для цитирования:
Цымай Ю.В. Метод выбора управляющего решения при диапазонных входных сигналах для детерминированно-стохастической модели. Вестник кибернетики. 2024;23(4):110–117. https://doi.org/10.35266/1999-7604-2024-4-11
For citation:
Tsymay Yu.V. Method for selecting management decision with range input signals for deterministic and stochastic model. Proceedings in Cybernetics. 2024;23(4):110–117. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-11
ВВЕДЕНИЕ
Основной задачей проектирования технических систем является повышение производительности. Если система построена на базе управляемого контроллера, то эту характеристику описывают через закон К. Мура, согласно которому каждые два года при определенной модификации управляющего устройства его производительность возрастает. Это привело к увеличению потенциала распараллеливания. Появилась необходимость использовать параллелизм за пределами уровня инструкций программируемого управляющего устройства. Несмотря на это, многие программы по-прежнему создаются последовательно, что затрудняет их эффективную работу при большом потоке данных. Большие данные и интернет вещей добавляют к проблеме эффективной параллелизации последовательной программы проблему эффективной обработки больших объемов данных. При проведении исследований очень важно быстро отличать существенные данные от неважных и, таким образом, сокращать объем обрабатываемых баз данных. При этом, по возможности, не должно быть потеряно никакой важной информации. Поскольку эти большие объемы данных генерируются многократно и непрерывно, необходимо увеличивать тактовую частоту, что предполагает не всегда возможную модернизацию микроконтроллера и периферийного блока. Задача здесь состоит в том, чтобы найти энергоэффективное решение, которое является гибким и масштабируемым для удовлетворения растущих объемов данных [1][2].
Ведущие производители технологических решений и поставщики облачных услуг, такие как Intel или Amazon, осознали эту проблему и среди прочего сделали ставку на технологию ПЛИС (программируемая интегральная логическая схема), поскольку она представляет собой производительную и энергоэффективную альтернативу многоядерным процессорам. Но для некоторых задач ПЛИС не является эффективной, т. к. многое зависит от типа обрабатываемых данных и аппаратной части управляемой технической системы [3, 4].
Реконфигурация требует времени, которое может быть недоступно для технических систем, работающих в режиме реального времени. Поэтому необходимо найти способ минимизировать или скрыть время реконфигурации и минимизировать количество необходимых реконфигураций. Кроме того, как и в случае с большинством новых технологий, до сих пор нет четкого представления о подходящей области применения и характеристиках, которые необходимо привнести в различные области, чтобы извлечь выгоду из этой технологии.
МАТЕРИАЛЫ И МЕТОДЫ
В начале 2000 г. была представлена концепция динамически реконфигурируемой системы. Она могла переключаться между 4 конфигурациями в течение одного тактового цикла, а дополнительные конфигурации могли быть загружены во время работы. Однако реконфигурируемые архитектуры имели некоторые ограничения, такие как длительное время перенастройки, жестко заданная форма конфигураций и нулевая поддержка режимов энергосбережения. Из-за этих ограничений разрабатываются архитектуры, методы разработки и инструменты, которые можно динамически перенастраивать, а также области применения динамической реконфигурации [5].
Но модернизация для программируемых систем ведет к повышению экономических затрат, глобальной перенастройке аппаратной части. Наиболее рациональным будет корректировка управляющей программы таким образом, чтобы ее можно было использовать для технических систем с неизбыточной периферией. Для реализации этой идеи применимы различные математические методы, которые позволят скорректировать управляющий алгоритм [6].
Метод Монте-Карло основан на выполнении большого числа случайных выборок для получения приближенных решений. Он широко используется в задачах, где невозможно получить точное аналитическое решение или оно сложно для вычисления. Этот метод работает следующим образом: определяется пространство поиска решений, генерируются случайные точки внутри этого пространства, вычисляются значения функции в каждой точке, результаты усредняются для получения окончательного результата. При большом потоке данных метод Монте-Карло может оказаться неэффективным из-за своей медленной сходимости. Постоянно меняющиеся входные параметры также усложняют получение стабильных результатов, так как каждое изменение требует нового набора случайных чисел и повторных вычислений [7].
Интервальный метод предназначен для нахождения гарантированных оценок решений в рамках заданных интервалов. Вместо точечного значения функция оценивается на всем интервале. Необходимо задание интервала для входных данных. Далее происходит оценка функции на всем интервале. Метод устойчив к погрешностям округления, но возникает эффект обертывания, приводящий к неограниченному росту ширины интервалов. Эффект обертывания становится серьезной проблемой при большом количестве данных и частых изменениях параметров, так как ширина интервалов может расти экспоненциально, делая результаты практически бесполезными. Это делает интервальные методы малоэффективными при исследовании детерминированных и стохастических систем [8, 9].
Метод Тейлора основан на разложении функции в ряд Тейлора для получения аппроксимации решения. Выполняется разложение функции в окрестности начальной точки. Используются несколько первых членов ряда Тейлора, оцениваются остаточные члены. Метод обладает высокой аналитической точностью, возможно использование функций высокого порядка. Но он не подходит для задач с большим потоком данных и постоянными изменениями параметров из-за высокой вычислительной сложности. Постоянные изменения параметров приводят к необходимости пересчета рядов Тейлора, что увеличивает нагрузку на ресурсы и замедляет процесс [10, 11].
Предлагаемая методика упрощает процесс анализа и отбора диапазонов данных с установленным приоритетом или уровнем актуальности, на основе которых формируется управляющее воздействие. Сегменты данных до исполнения алгоритма отбора не имеют определенного приоритета или иерархии по старшинству. Принимается допущение, что их объем меняется в любой момент времени, но сами изменения фиксируются в конце исследуемого временного промежутка. Это позволит описывать поведение системы интервальной шкалой времени. Цена деления такой шкалы будет соответствовать целому постоянному временному интервалу (Т), в пределах которого фиксируются изменения в динамической системе.
Размеры сегментов данных меняются по двум событиям. Первое событие связано с наличием потоков, направленных в систему. Второе событие инициируется внутренним перемещением между сегментами. Из базового сегмента некоторое количество данных nij(T) перемещается в соседний сегмент в следующий момент времени. Некоторое количество данных njk+1(T) исключается из базового сегмента как неактуальное. Тогда набор данных в текущем сегменте в следующий момент состоит из оставшихся, прошедших критериальный отбор, значений и вновь появившихся актуальных данных n0i(Т + 1).
В результате можно описать состояние потока входных данных в результате критериального отбора в текущий и следующий момент времени (1):
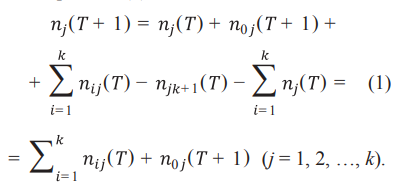
Число оставшихся в базовом сегменте данных будет определяться по формуле (2):
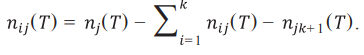 (2)
(2)
Потоки перехода между сегментами отобранных данных управляются совокупностью факторов:
– количество переходов связано с вакантным диапазоном nik+1(T);
– автоматический переход в связи с повышением актуальности.
Последнее будет выбрано основным допущением модели в связи с большей вероятностью осуществления в реальной системе. Тогда соотношение между потоками и уже классифицированными данными определяется как nij(T)/ni(T) (i = 1, 2, …, k + 1) и является константой (если в модели не учитывать статистические колебания).
Спрогнозируем размеры диапазонов данных. Если учитывать коэффициент пропорциональности, то модель детерминированная, но когда ее свойства не будут адекватны реальной системе и модель будет генерировать неточные данные для долгосрочного моделирования, то есть появятся значительные изменения при разных ni(T) (уход одного значения из базы данных не предсказуем), то есть в модели появляется элементы стохастичности.
Поэтому необходимые методы теории вероятности, которая позволит количественно оценить неопределенности. Допустим, что перемещения в сегментах данных не связаны между собой причинно-функциональной зависимостью. Отдельные данные в исходном сегменте характеризуется вероятностью pij-перехода в следующий сегмент в течение одного момента времени по установленной временной шкале. Вероятность ухода одного из значений ωi будет определяться статистической выборкой [12]. Тогда такое развитие событий описывается формулой (3):
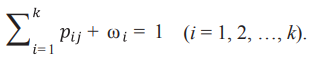 (3)
(3)
Отдельные данные могут оставаться в уже занятом сегменте, а при изменении критериев отбора переместиться в следующий сегмент или покинуть базу данных в связи с неактуальностью.
Новый набор данных будет описываться по формуле (4) общим количественным входным потоком и способом распределения по сегментам. Если входной поток является фиксированной величиной, то число новых данных соответствует числу выбывших:
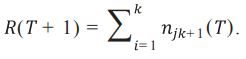 (4)
(4)
Распределение новых данных описывается формулой (5) и соответствует допущениям, принятым выше:
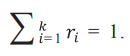 (5)
(5)
Модель поведения данных в сегментированном хранилище при изменении их актуальности позволила:
– учесть детерминированные и стохастические характеристики технической системы;
– применить генетический алгоритм, используемый для формирования и корректировки управляющего сигнала.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Для тестирования предлагаемого алгоритма использовалась модель системы управления движущимся объектом (рис. 1 а). В качестве пути рассматривалось прохождение произвольной траектории в лабиринте (рис. 1 б).
Объект управления получал управляющий сигнал от устройства управления о начале движения. Его координаты фиксировались посредством датчиков, наличие препятствий определялось через срабатывание датчиков. В данном эксперименте можно выделить следующие параметры: входные сигналы хi, описывающие момент срабатывания датчиков; выходные сигналы yj, описывающие результат срабатывания системы; основные события в системе. Состояния системы меняются в результате появления любого входного сигнала и полностью совпадают со значениями yj, поэтому здесь они не описываются. Определены основные события в системе:
- Начало процесса движения.
- Получение контрольного сигнала с датчика о препятствии.
- Контрольный сигнал.
- Изменение положения объекта управления (поворот или поступательное движение с реверсом).
- Движение по новой траектории.
Каждое событие инициируется набором входных сигналов хi. Наличие того или иного сигнала соответствует логической единице. Фрагмент псевдокода вероятностной модели скоростного движения объекта управления показан на рис. 2. Результаты реакции на препятствие без корректирующего алгоритма показаны на рис. 3. Реализация процесса цифровой фильтрации данных на основе генетического алгоритма и результаты тестирования показаны на рис. 4.
Алгоритм строится на базе знания о весе каждой точки входного сигнала и процессе распределения по методу генетического отбора через программируемую функцию взвешивания. Результаты тестирования измененного входного сигнала показывают определение препятствий с большей точностью, что позволило выстроить относительно равномерную траекторию движения объекта управления.
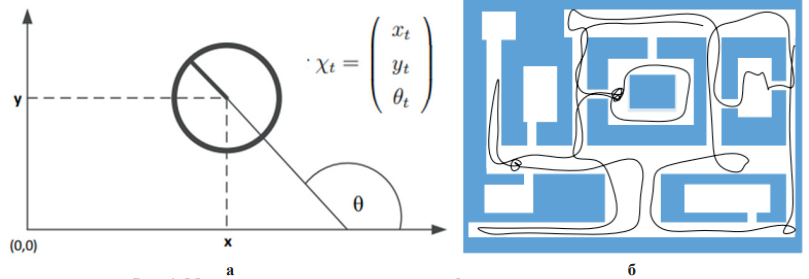
Рис. 1. Модель управления движущимся объектом с учетом траектории:
а – модель системы управления движущимся объектом; б – произвольной траектории в лабиринте
Примечание: составлено автором на основании данных, полученных в исследовании.
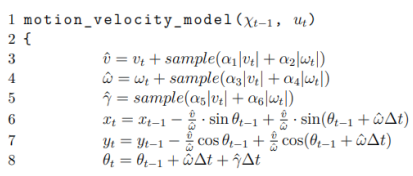
Рис. 2. Фрагмент псевдокода вероятностной модели скоростного движения объекта управления
Примечание: составлено автором на основании данных, полученных в исследовании.
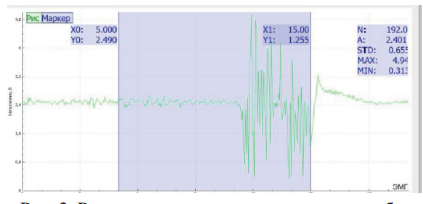
Рис. 3. Результаты реакции на препятствие без корректирующего алгоритма
Примечание: составлено автором на основании данных, полученных в исследовании.
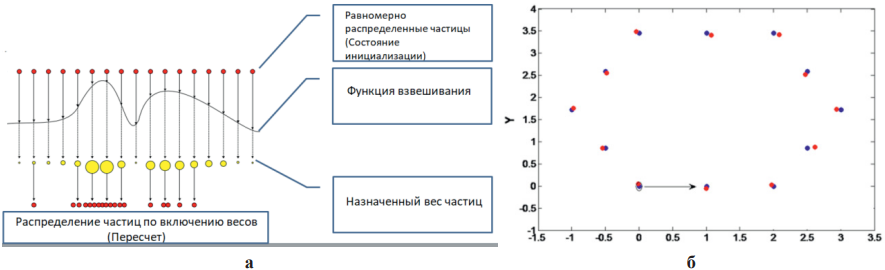
Рис. 4. Реализация процесса цифровой фильтрации данных: а – алгоритм фильтрации, б – апробация после фильтрации
Примечание: составлено автором на основании данных, полученных в исследовании.
ЗАКЛЮЧЕНИЕ
Таким образом, в рамках исследования раскрыты основные аспекты, использующиеся при исследовании динамических систем с неопределенными параметрами, приведены сферы их применения; описан алгоритм формирования диапазонов данных в зависимости от их актуальности для динамической системы. Выполнен анализ методов, которые используются при моделировании процессов функционирования сложных технических систем, изучены возможные способы их применения; проведен детальный анализ методов, которые используются при моделировании процессов с неопределенными параметрами, меняющимися в процессе функционирования или при запуске нового цикла; изучены и описаны наиболее важные факторы, влияющие на процессы корректировки управляющего сигнала. Рассмотрены средства моделирования динамических систем.
В дальнейшем необходимо описать критерии оценки динамических систем с неопределенными параметрами, выбрать наиболее существенные параметры для моделирования и оценки; выполнить анализ внешних помех и степень их влияния на динамическую систему с неопределенными параметрами; выполнить численный анализ изменения внутренних состояний технической системы под воздействием внешних факторов; выполнить анализ степени влияния динамических параметров на статические характеристики, произвести корректировку констант; выполнить моделирование поведения системы в предельных диапазонах, определить критические точки работы технической системы; выполнить анализ неопределенных параметров, вызывающих случайное поведение технической системы. Это позволит более точно выполнить программную реализацию алгоритмов исследования состояний имитационной модели многокомпонентной динамической системы с неопределенными параметрами.
Список литературы
1. Nyrkov A. P., Kardakova M. V., Kolesnichenko S. V. et al. Modeling the Operating Range of the Fire Safety System Response Parameters on Board. In: 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), January 27–30, 2020, St. Petersburg and Moscow, Russia. 2020. p. 434–437. https://doi.org/10.1109/EICon-Rus49466.2020.9038955.
2. Борисов А. В. Алгоритм робастной фильтрации марковских скачкообразных процессов по высокочастотным считающим наблюдениям // Автоматика и телемеханика. 2020. № 4. С. 3–20.
3. Афанасьева О. В., Колесниченко С. В., Новожилов И. М. Теоретические аспекты анализа структурных сдвигов при исследовании процессов динамики сложных технических и социально-экономических систем // Инновации. 2018. № 10. С. 108–112.
4. Железнов Э. Г., Комиссаров П. В., Цымай Ю. В. Исследование эргатических систем управления // Современные наукоемкие технологии. 2021. № 4. С. 37–41.
5. Васильев Ф. П., Иваницкий А. Ю. Линейное программирование. М. : МЦНМО, 2020. С. 412.
6. Колесниченко С. В. Исследование подходов по оценке качества сложных технических систем на различных стадиях разработки // Записки Горного института. 2014. Т. 208. С. 244–248.
7. Железнов Э. Г., Пахарев М. Д., Колесниченко С. В. и др. Модель оценки процессов функционирования сложного транспортного предприятия : патент 2021617682 Рос. Федерация № 2021616649 ; заявл. 28.04.2021 ; опубл. 18.05.2021. URL: https://www. elibrary.ru/download/elibrary_45823909_50270059. PDF (дата обращения: 15.11.2024).
8. Srivastava N., Hinton, G., Krizhevsky A. et al. Drop- out: A simple way to prevent neural networks from overfi tting // Journal of Machine Learning Research. 2014. Vol. 15. P. 1929–1958.
9. Абрамов О. В. Дестабилизирующие факторы и случайные процессы изменения параметров технических устройств и систем // Надежность и качество сложных систем. 2024. № 1. С. 13–20.
10. Курганов В. М., Дорофеев А. Н., Грязнов М. В. Функционал путевого листа в transportation management system // Вестник СибАДИ. 2022. Т. 19, № 2. С. 216–223. https://doi.org/10.26518/2071-7296-2022-19-2-216-223.
11. Иваненко В. И. Применение технологий big data в принятии управленческих решений и повышении эффективности бизнеса // Стратегии развития социальных общностей, институтов и территорий : материалы IX Междунар. науч.-практ. конф. в 2-х т., 17–18 апреля 2023 г., г. Екатеринбург. Уральский федеральный университет имени первого Президента России Б. Н. Ельцина, 2023. Т. 1. С. 31–36.
12. Budkov Yu. A., Sergeev A. V., Zavarzin S. V. et al. Two-component electrolyte solutions with dipolar cations on a charged electrode: Theory and computer simulations // Journal of Physical Chemistry C. 2020. Vol. 124, no. 30. P. 16308–16314.
Об авторе
Ю. В. ЦымайРоссия
аспирант, ассистент кафедры математического моделирования и прикладной информатики, старший преподаватель
Рецензия
Для цитирования:
Цымай Ю.В. Метод выбора управляющего решения при диапазонных входных сигналах для детерминированно-стохастической модели. Вестник кибернетики. 2024;23(4):110–117. https://doi.org/10.35266/1999-7604-2024-4-11
For citation:
Tsymay Yu.V. Method for selecting management decision with range input signals for deterministic and stochastic model. Proceedings in Cybernetics. 2024;23(4):110–117. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-11















