Перейти к:
Триангуляция методом измельчения плоской области, заданной системой неравенств
https://doi.org/10.35266/1999-7604-2025-1-2
Аннотация
На текущий момент времени актуализируется интеграция компьютерных технологий практически во всех, как бытовых, так и профессиональных, сферах жизнедеятельности человека. В связи с этим происходит активное развитие новых средств и методов решения задач посредством использования цифровых и информационных технологий. Одним из наиболее актуальных направлений развития является компьютерная геометрия. На текущий момент существует ряд задач, требующих решения в данной области, одной из которых является триангуляция методом измельчения плоской области, заданной системой неравенств. Основной целью представленной статьи является разработка и программная реализация алгоритма триангуляции, основанного на методе измельчения плоской области, заданной системой неравенств. В результате работы проанализированы различные алгоритмы триангуляций, в том числе алгоритма измельчения плоской области, заданной системой неравенств. Проведен анализ схемы работы приложения, а также проанализированы способы его применения. Теоретическая значимость исследования заключается в изучении общих понятий, свойств и алгоритмов триангуляции. Практическая значимость исследования состоит в приведении программной реализации алгоритма измельчения плоской области. Результаты работы могут быть использованы в последующих исследованиях, подразумевающих необходимость применения триангуляции методом измельчения плоской области.
Ключевые слова
Для цитирования:
Зорькин Д.Ю., Тарасова И.А., Клячина Н.В. Триангуляция методом измельчения плоской области, заданной системой неравенств. Вестник кибернетики. 2025;24(1):11-18. https://doi.org/10.35266/1999-7604-2025-1-2
For citation:
Zorkin D.Yu., Tarasova I.A., Klyachina N.V. Triangulation of plane domain by grinding method defined by system of inequalities. Proceedings in Cybernetics. 2025;24(1):11-18. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-2
ВВЕДЕНИЕ
Основной целью статьи является разработка и программная реализация алгоритма триангуляции, основанного на методе измельчения плоской области, заданной системой неравенств. В рамках статьи решается ряд задач, каждой из которых посвящены отдельные разделы работы – рассмотрение основных понятий и определений триангуляции, а также выполнение разработки и тестирования программы на языке программирования Python с представлением визуальных примеров.
МАТЕРИАЛЫ И МЕТОДЫ
Пусть имеется множество точек, которое изначально представляет собой набор вершин графа. Необходимо провести такие ребра, чтобы все внутренние области графа образовывали треугольники. Триангуляция представляет собой плоский граф, каждая внутренняя область которого является треугольником [1]. Также данный метод триангуляции применим для разбиения фигур в многомерных пространствах (рис. 1). Существует множество различных подходов и методов для разделения областей на треугольники [2].
Выпуклая триангуляция представляет собой триангуляцию, в которой минимальный многоугольник, охватывающий все треугольники, является выпуклым.
Такая невыпуклая триангуляция называется невыпуклой [3].
Задачи построения триангуляции заключаются в следующем: пусть задан такой набор точек, что, расположив его на плоскости, каждая точка будет иметь две координаты: (x, y). Нужно, чтобы эти точки были соединены таким образом, чтобы в результате получилась триангуляция [4].
Перед тем как углубляться в подробное изучение метода измельчения, нужно рассмотреть основную суть алгоритма. Рассмотрим на примере произвольной области, ограниченной кривыми. Для корректного выполнения триангуляции области точки, находящиеся на границе триангуляции внутри области, должны смещаться к границам области с использованием градиентного спуска по следующей формуле (1):
(x1, y1) = (x0, y0) + α * gradF(x0, y0),(1)
где α – сдвиг с определенным шагом;
(x0, y0) – начальные координаты точек;
gradF – градиентная функция;
F(x; y) – функция, зависящая от двух переменных.
Точки (x1, y1) представляют собой новые координаты исходных точек (x0, y0) после их сдвига по заданной формуле.
Сдвиг выполняется для того, чтобы точки приблизились к границам области, не выходя за их пределы [5].
Рассмотрим алгоритм измельчения триангуляционной области более подробно.
Дано конечное множество точек {Pi} в плоскости R² и триангуляция T = {Tj}, где каждый треугольник содержит три точки из {Pi}, а каждая точка является вершиной хотя бы одного треугольника. Обозначим минимальный угол триангуляции как α(T). Объединение всех треугольников образует многоугольник. Пусть Ω – ограниченная область в R²; триангуляцией области Ω называется триангуляция конечного набора точек в замыкании Ω. Треугольники с двумя или тремя вершинами на границе ∂Ω называются граничными, остальные – внутренними [6].
Для построения треугольной сетки предлагаем подход с одним проходом по вершинам: выбираем небольшое количество точек из Ω и строим начальную триангуляцию, затем применяем процесс измельчения для повышения точности. Качество триангуляции определяется минимальным синусом углов треугольников, что влияет на погрешность при вычислении функций и их производных. Алгоритм измельчения состоит из следующих последовательных шагов [7]:
- Зафиксируем натуральное число q.
- Для каждого внутреннего треугольника Tk:
– выбираем одну из его вершин;
– делим стороны, выходящие из этой вершины, на q равных отрезков;
– проводим через полученные точки прямые, параллельные другим сторонам треугольника;
– в результате треугольник Tk разбивается на q² подобных треугольников.
При таком разбиении минимальный угол новой триангуляции остается равным (рис. 2) α(T), обеспечивая высокое качество сетки и более точное приближение границы области.
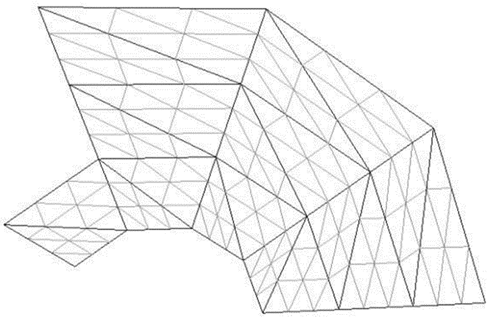
Рис. 1. Вид триангуляции
Примечание: составлено авторами.
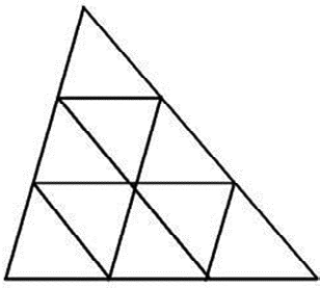
Рис. 2. Разбиение треугольника на 9 подобных треугольников (q = 3)
Примечание: составлено авторами.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Отдельно рассмотрим программную реализацию алгоритма измельчения.
Данная программа выполняет триангуляцию области, ограниченной функциями F1(x) и G1(x), измельчение треугольников и применение градиентного спуска к крайним точкам триангуляции.
В качестве примеров, рассмотрим области, ограниченные неравенствами.
Пример 1 (2):
y ≥ x 2; y ≤ 1. (2)
Из данного неравенства следует, что нижняя функция ограничена параболой, а верхняя функция ограничена прямой.
Далее программа осуществляет вывод следующих графиков.
На изображении (рис. 3) также видны следующие элементы:
- Синие точки – начальные точки для триангуляции.
- Фиолетовые линии – границы треугольников начальной триангуляции.
- Красная линия – граница области y= x2.
- Синяя горизонтальная линия – граница области y= 1.
В частности, это изображение соответствует начальной стадии построения триангуляции перед применением алгоритма измельчения. Граничные точки размещены так, что они образуют три треугольника, полностью лежащих внутри заданной области [8].
На изображении (рис. 4) демонстрируется триангуляция после применения алгоритма измельчения до сдвига точек, находящихся на границе триангуляции внутри области.
Процесс измельчения заключается в следующем:
- Для каждой стороны начального треугольника вычисляется средняя точка.
- Эти средние точки добавляются как новые вершины.
- Затем начальный треугольник делится на несколько более мелких треугольников, используя новые средние точки [9].
В результате после применения алгоритма измельчения количество треугольников увеличивается, что приводит к более детализированной и точной триангуляции. Визуальный результат:
- Вершины новых треугольников отмечены синими точками.
- Границы новых треугольников отмечены фиолетовыми линиями.
На графике (рис. 5) показана триангуляция Делоне для точек, перемещенных по градиенту функции F(x; y). Точки снова отмечены синим цветом, а треугольники образованы ребрами пурпурного цвета. Границы области остаются теми же (красная и синяя линии). Точки были перемещены по градиенту, не выходя за границы области.
Этот график (рис. 6) показывает сдвиг точек с помощью стрелок, указывающих направление и величину перемещения. Исходные точки отмечены синим цветом. Стрелки, нарисованные зеленым цветом, показывают сдвиг каждой точки.
Описание:
- Синие точки представляют исходные координаты.
- Зеленые стрелки указывают направление и величину сдвига точек. В некоторых случаях стрелки могут быть очень короткими или отсутствовать, если точки остались на месте (например, точки на границах).
Пример 2 (3):
y – x 2 > 0; y – x < 0. (3)
Из данного неравенства следует, что нижняя функция ограничена параболой, а верхняя функция ограничена прямой.
На этом изображении (рис. 7) показана начальная триангуляция области, ограниченной параболой и прямой. Синие точки показывают начальные узлы, и треугольники построены на основе этих точек.
На этом изображении (рис. 8) показана триангуляция после измельчения начальных треугольников. Дополнительно введенные точки (на серединах ребер начальных треугольников) добавлены, что привело к увеличению количества треугольников. Этот процесс увеличивает число разбиений в области и обеспечивает более точное представление геометрии области.
На этом подграфике показана триангуляция после применения градиентного спуска к граничным точкам. Точки на границе перемещаются под действием градиентных сил, чтобы лучше соответствовать граничным условиям. Сравнение с предыдущим подграфиком показывает, что точки и треугольники были смещены ближе к реальным границам. Триангуляция после сдвига точек представлена на рис. 9 и 10 соответственно.
Пример 3 (криволинейная трапеция).
Пусть Ω – плоская область, которая будет задана при помощи системы неравенств (4):
0 ≤ x ≤ 3,
{x 2 – 3 × x – 2 ≤ y ≤ 3 × x – x 2}. (4)
Получится следующая триангуляция криволинейной трапеции, построенная при помощи алгоритма измельчения (рис. 11–12).
Разработанный в рамках исследования алгоритм триангуляции основывается на методе измельчения плоской области, ограниченной системой неравенств. Этот подход был реализован с помощью программной реализации, обеспечил высокую точность построения триангуляции благодаря градиентному сдвигу точек к границам области [10].
Графики, представленные на рис. 3–12, демонстрируют эффективность предложенного метода. Использование измельчения позволило значительно увеличить количество треугольников в пределах области, тем самым обеспечив более детализированную и точную аппроксимацию ее границ.
Интересно сравнение этого метода с классическим алгоритмом Делоне. Алгоритм измельчения показывает явные преимущества при обработке областей с большим разбиением треугольников. В частности, по сравнению с исследованиями А. В. Скворцова, который акцентировал внимание на триангуляции Делоне для ограниченных областей, метод измельчения позволяет более точно контролировать форму и расположение граничных треугольников за счет применения градиентного сдвига [10].
Стоит отметить, что минимальный угол треугольников триангуляции, как было показано в исследованиях А. А. Клячина, влияет на точность вычислений при аппроксимации функций на этой триангуляции. Наши результаты подтверждают, что применение метода измельчения позволяет сохранять достаточно высокие значения минимальных углов треугольников, что способствует уменьшению погрешности вычислений. Однако, как и в любом численном методе, существует ряд ограничений. Во-первых, эффективность алгоритма напрямую зависит от начального распределения точек и формы области. В некоторых случаях, когда область имеет сложную форму или большое количество точек на границе, алгоритм может требовать значительных вычислительных ресурсов. Во-вторых, при очень мелкой триангуляции может возникать проблема накопления ошибок при многократном измельчении, что требует дополнительной оптимизации на стадии градиентного сдвига точек.
В дальнейшем планируется исследовать возможности комбинирования метода измельчения с другими подходами к триангуляции, а также расширение программы для работы с многомерными областями.
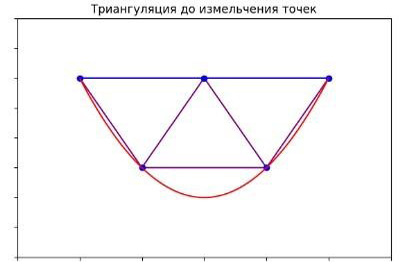
Рис. 3. Первоначальная триангуляция до сдвига точек
Примечание: составлено авторами.
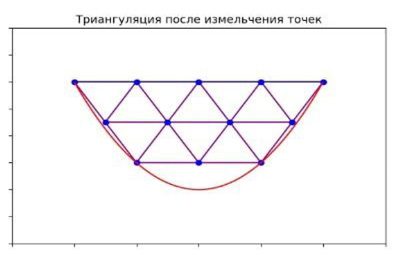
Рис. 4. Триангуляция после применения алгоритма измельчения
Примечание: составлено авторами.
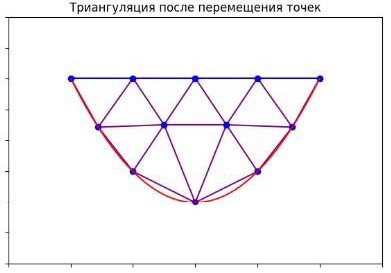
Рис. 5. Триангуляция после применения алгоритма измельчения
Примечание: составлено авторами.
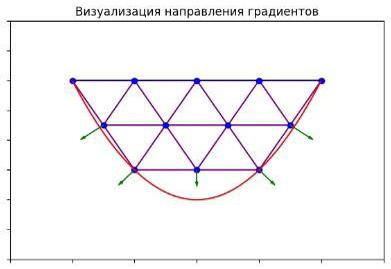
Рис. 6. Визуализация градиентов сдвига
Примечание: составлено авторами.
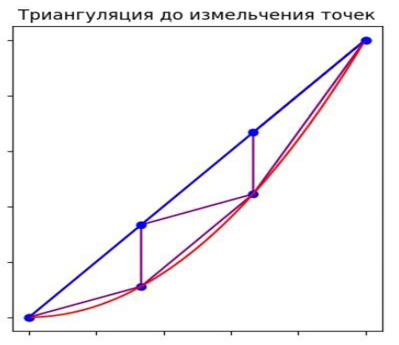
Рис. 7. Первоначальная триангуляция до применения алгоритма
Примечание: составлено авторами.
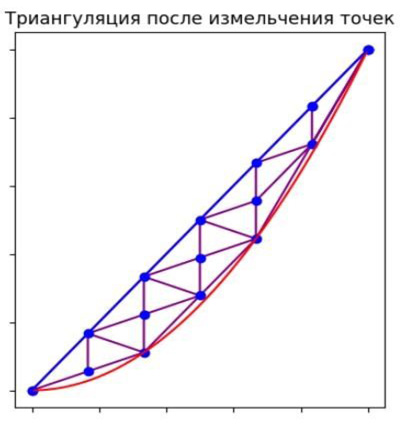
Рис. 8. Алгоритм измельчения до сдвига точек
Примечание: составлено авторами.
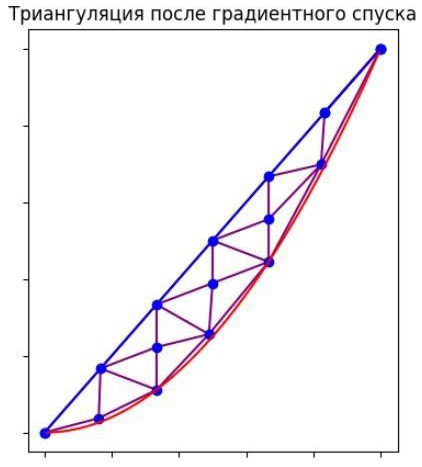
Рис. 9. Триангуляция после сдвига точек
Примечание: составлено авторами.
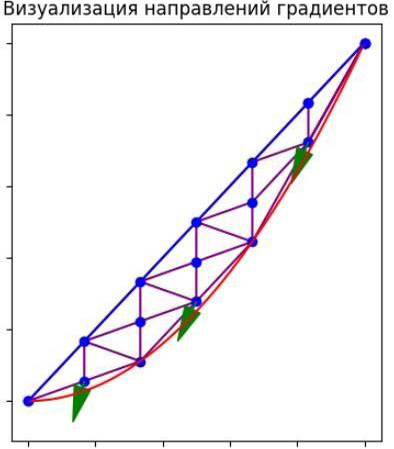
Рис. 10. Триангуляция после сдвига точек
Примечание: составлено авторами.
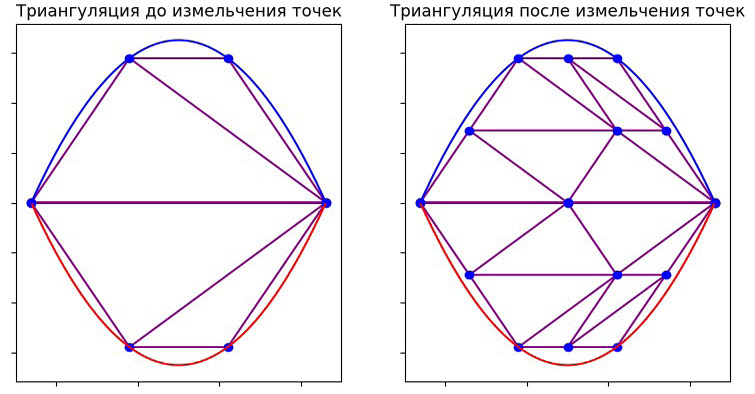
Рис. 11. Триангуляция до применения и после применения алгоритма измельчения до сдвига точек
Примечание: составлено авторами.
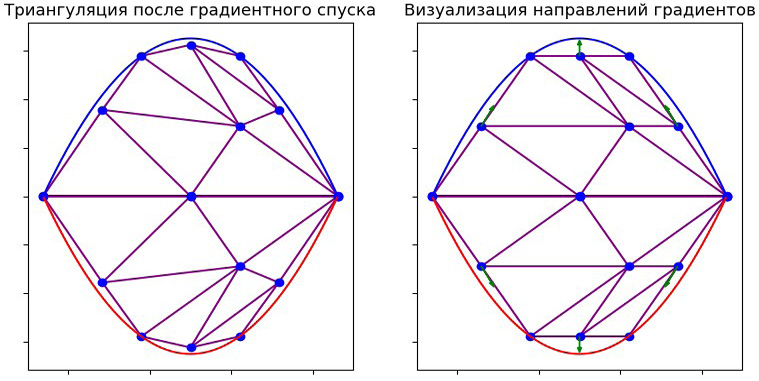
Рис. 12. Триангуляция после сдвига точек (предоставлена визуализация направления градиентов)
Примечание: составлено авторами.
ЗАКЛЮЧЕНИЕ
Таким образом, основной целью представленной работы являлось выполнение разработки и программной реализации алгоритма триангуляции, основанного на методе измельчения плоской области, заданной системой неравенств. Триангуляция применяется как эффективный метод разбиения, в частном случае это алгоритм измельчения произвольной триангуляционной поверхности. В заключение необходимо отметить, что триангуляция может применяться в таких областях, как медицина, физика, химия и другие научные сферы.
Триангуляция является основным методом создания геодезических сетей на большой территории и по сей день, только сейчас эти алгоритмы разбиения непосредственно применяются не вручную, а при помощи различных программных инструментов. Ведь процесс ручной триангуляции является более долгим, чем с помощью программ. Этим обуславливается актуальность данной темы. Результаты работы могут быть применены при решении различных практических задач в профессиональных сферах жизнедеятельности человека.
Список литературы
1. Грузинцев И. О., Якобовский М. В. Алгоритмы адаптивного измельчения трехмерных расчетных сеток // Параллельные вычислительные технологии (ПАВТ’2019) : Короткие статьи и описания плакатов XIII Междунар. науч. конф., 02–04 апреля 2019 г., г. Калининград : Издательский центр ЮУр-ГУ. С. 223–231.
2. Мендакулов Ж. К. Анализ чувствительности алгоритма триангуляции к ошибкам в измерении углов для задач определения местоположения внутри помещений // Вестник Алматинского университета энергетики и связи. 2019. № 3. С. 26–34.
3. Клячин А. А. Построение триангуляции плоских областей методом измельчения // Вестник Волгоградского государственного университета. Серия 1, Математика. Физика. 2017. № 2. С. 18–28.
4. Бородин О. В., Иванова А. О. Комбинаторное строение граней в триангуляциях на поверхностях // Сибирский математический журнал. 2022. Т. 63, № 4. С. 796–804.
5. Скворцов А. В. Обзор алгоритмов построения триангуляции Делоне // Вычислительные методы и программирование. 2002. Т. 3, № 1. С. 14–39.
6. Петрова М. А., Синельщикова О. Ю. Триангуляция в системе Li2ZNP2O7–Na2ZNP2O7–K2ZNP2O7 // Журнал неорганической химии. 2022. Т. 67, № 2. С. 216–223.
7. Перевезенцев В. Н., Кириков С. В., Свирина Ю. В. Анализ условий формирования деформационной фасетки при взаимодействии плоского скопления решеточных дислокаций с границей зерна // Физика металлов и металловедение. 2020. Т. 121, № 10. С. 1019–1025.
8. Фроленков С. А. Применение метода триангуляции для диагностики контактной сети // Наука и образование транспорту. 2020. № 1. С. 365–368.
9. Клячин В. А., Широкий А. А. Триангуляция Делоне многомерных поверхностей // Вестник СамГУ – Естественнонаучная серия. 2010. № 4. С. 51–55.
10. Скворцов А. В. Алгоритмы построения триангуляции с ограничениями // Вычислительные методы и программирование. 2002. Т. 3, № 1. С. 82–92.
Об авторах
Д. Ю. ЗорькинРоссия
преподаватель
И. А. Тарасова
Россия
заведующий кафедрой, доцент
Н. В. Клячина
Россия
старший преподаватель
Рецензия
Для цитирования:
Зорькин Д.Ю., Тарасова И.А., Клячина Н.В. Триангуляция методом измельчения плоской области, заданной системой неравенств. Вестник кибернетики. 2025;24(1):11-18. https://doi.org/10.35266/1999-7604-2025-1-2
For citation:
Zorkin D.Yu., Tarasova I.A., Klyachina N.V. Triangulation of plane domain by grinding method defined by system of inequalities. Proceedings in Cybernetics. 2025;24(1):11-18. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-2















