Перейти к:
Имитационное моделирование и анализ систем массового обслуживания
https://doi.org/10.35266/1999-7604-2025-1-8
Аннотация
Основное внимание в рассматриваемой статье уделяется системам с фиксированным максимальным числом требований, ожидающих обслуживания. Это означает необходимость учета не только наличия очереди, но и ее конечной емкости, что добавляет сложности в анализ подобных систем. Введение таких ограничений может привести к более реалистичным моделям, отражающим реальные условия эксплуатации систем массового обслуживания. Понимание основных концепций теории массового обслуживания помогает не только структурировать исследование, но и определить направления для дальнейших разработок. В статье представлено изучение существующих моделей и систем массового обслуживания с целью выявления лучших практик и возможных недостатков. Сравнительный анализ позволяет не только адаптировать проверенные решения под новые условия, но и избежать ошибок прошлых исследований.
Ключевые слова
Для цитирования:
Богнюков А.А., Зорькин Д.Ю., Шведов Е.Г. Имитационное моделирование и анализ систем массового обслуживания. Вестник кибернетики. 2025;24(1):53-59. https://doi.org/10.35266/1999-7604-2025-1-8
For citation:
Bognyukov A.A., Zorkin D.Yu., Shvedov E.G. Simulation modeling and analysis of queuing systems. Proceedings in Cybernetics. 2025;24(1):53-59. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-8
ВВЕДЕНИЕ
Основной целью статьи является изучение и анализ областей применения и особенностей имитационного моделирования. Актуальность работы обусловлена растущей сложностью современных систем и процессов. Современные системы становятся все более сложными и взаимосвязанными, что затрудняет их анализ. Имитационное моделирование позволяет исследовать эти системы в виртуальной среде, проводить эксперименты и анализировать результаты без риска для реальной инфраструктуры или оборудования.
Большинство изучаемых и подлежащих моделированию объектов являются сложными системами, и это утверждение можно считать фундаментальным в контексте современных исследований и разработок. Сложные системы характеризуются множеством факторов, которые делают их изучение особенно интересным и одновременно трудным. Одним из главных признаков сложной системы является невозможность рассмотрения ее элементов в изоляции [1]. Это объясняется тем, что каждый элемент тесно взаимосвязан с другими элементами системы и с внешней средой, что приводит к необходимости учитывать широкий спектр связей и взаимодействий при анализе таких систем.
Оптимизация производственных процессов является одной из ключевых областей применения имитационного моделирования, особенно в контексте современной промышленности, где эффективность и эффективное использование ресурсов становятся все более важными для конкурентоспособности компаний [2].
В рамках статьи решается ряд задач, каждой из которых посвящены отдельные разделы работы – анализ конкретных примеров применения имитационного моделирования в различных сферах, оценка эффективности имитационного моделирования и определение потенциальных направлений для дальнейшего развития имитационного моделирования.
МАТЕРИАЛЫ И МЕТОДЫ
Следует рассмотреть схему моделируемого процесса (рис. 1).

Рис. 1. Схема моделируемой системы массового обслуживания
Примечание: составлено авторами.
Входящее требование должно пройти через один из каналов обслуживания (А или B), при этом у них есть общая очередь (О1). После этого требования обслуживаются на канале обслуживания C (с очередью О2). Требования, пришедшие в момент, когда очередь достигла максимальной длины, покидают систему.
Была построена имитационная модель системы: за шаг дискретизации времени было взято время, равное 1 сек. Предположим, что в данный период не может произойти более одного события. Также построена блок-схема и произведен расчет за 30 минут. По результатам расчета найдена доля покупателей и средняя доля времени простоя прилавков. На экране выведено число отказов и их доля.
λ = 3
– макс. значение О1 = 2;
– макс. значение О2 = X;
– μА = 1;
– μB = 3;
– μC = X.
Следует рассмотреть концептуальную схему моделируемой системы массового обслуживания, представленную на рис. 2.

Рис. 2. Концептуальная схема моделируемой системы массового обслуживания
Примечание: составлено авторами.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Результатом исследования является построенный граф состояний системы с учетом вводных данных (рис. 3).
Была построена система уравнений для равновесного состояния:

– p000 = 0.154589371980676;
– p010 = 0.231884057971014;
– p001 = 0.0772946859903382;
– p011 = 0.231884057971014;
– p111 = 0.173913043478261;
– p211 = 0.130434782608696.
Была найдена доля простоя первого канала обслуживания. Это сумма вероятности нахождения системы в состоянии, когда первый канал обслуживания простаивает, или p000 + p001.
Pпростоя канала A = p000 + p001 = 0,154589371980676 + 0,0772946859903382 = 0,23188405797.
23,19 % времени с момента равновесного состояния будет простаивать первый канал обслуживания.
Найдена доля простоя второго канала обслуживания. Это сумма вероятности нахождения системы в состоянии, когда второй канал обслуживания простаивает, или p000 + p010.
Pпростоя канала B = p000 + p010 = 0,154589371980676 + 0,231884057971014 = 0,38647342995.
38,65 % времени с момента равновесного состояния будет простаивать второй канал обслуживания.
Была просчитана средняя доля простоя каналов.

Просчитаем долю отказов:
Pотказа = p211 = 0,130434782608696.
13 % времени пришедшие требования будут уходит в отказ, или доля пришедших заказов равна 0,13. В среднем p211*λ = 0,130434782608696*3=
= 0,39130434782 требований будет уходить в отказ за единицу времени.
Посчитана средняя доля обслуженных требований. Это сумма пришедших требований минус количество требований ушедших в отказ, или 3–0,39130434782 = 2,60869565218.
Pобслуживания = 1 – pотказа = 1–0,130434782608696 = = 0,86956521739.
87 % пришедших требований будет обслужено.
Код был написан на языке программирования Python, а также проведен запуск программы и анализ полученных результатов (рис. 4–6).
Было установлено, что канал А простаивает реже, хотя ожидалось обратное, согласно чему напрашивается вывод о высокой производственной загрузке и повышенной эффективности производства. Канал В, напротив, простаивает больше ожидаемого. В отношении средних показателей доля простоев ниже, чем ожидалось, а средняя доля отказов выше ожидаемых значений. При этом на такие показатели доли отказов указывают перегрузы системы. Обслуженные требования имеют взаимосвязь с долей отказов, что говорит о приближенных значениях к ожидаемым показателям.
Был проведен повторный запуск программы (рис. 7–9).
При повторном запуске характеристики канала А и В остались неизменными. Доля простоев также оказалась, как и при первом запуске, ниже ожидаемых значений. Доля отказов существенно ниже ожидаемой, что является признаком высокой пропускной способности системы или улучшенной эффективности процессов обслуживания. Можно сделать вывод, согласно которому в условиях, когда нагрузка распределяется равномерно, система способна обрабатывать большее количество задач за единицу времени без возникновения узких мест или перегрузок. Это позволяет максимизировать использование доступных ресурсов и повысить общую эффективность работы.
Для достижения состояния равновесия и повышения точности прогнозируемых значений рекомендуется продлить время работы системы. Длительное функционирование позволит системе стабилизироваться и приблизиться к теоретически предсказанным показателям работы. В условиях равновесного состояния система демонстрирует более высокую надежность и воспроизводимость результатов, что крайне важно для имитационных моделей.

Рис. 3. Граф состояний системы
Примечание: составлено авторами.

Рис. 4. Результат выполнения программы
Примечание: составлено авторами.

Рис. 5. График количества требований в очереди на конец каждой минуты
Примечание: составлено авторами.

Рис. 6. График количества отказов на конец каждой минуты
Примечание: составлено авторами.
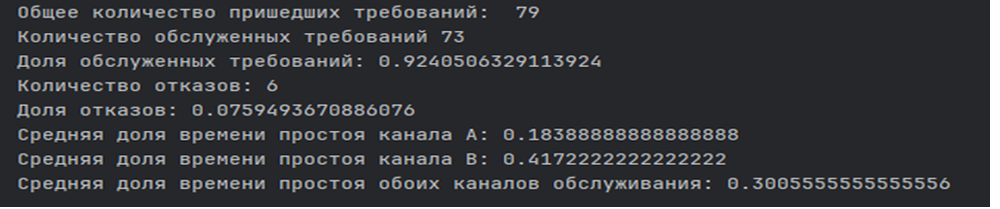
Рис. 7. Результат повторного запуска программы
Примечание: составлено авторами.

Рис. 8. График количества требований в очереди на конец каждой минуты
Примечание: составлено авторами.

Рис. 9. График количества отказов на конец каждой минуты
Примечание: составлено авторами.
ЗАКЛЮЧЕНИЕ
Таким образом, имитационные модели играют важную роль в предсказании поведения сложных систем и позволяют выявить узкие места до их возникновения в реальных условиях эксплуатации. Успешная работа такой модели свидетельствует о правильности выбранных стратегий управления и возможности их применения для оптимизации реальных систем в будущем.
Список литературы
1. Бакаева О. А., Сафонов В. И. Моделирование си-стем массового обслуживания с использованием сред программирования // Актуальные проблемы математики, механики, естествознания и образования. 2021. С. 28–33.
2. Линкина А. В., Блинов Р. А. Моделирование систем массового обслуживания (на примере решения задач геопространственной обработки данных) // Вестник Воронежского института высоких технологий. 2021. № 1. С. 36–38.
3. Астраханцева И. А., Горев С. В., Астраханцев Р. Г. Фрактальный анализ в оценке эффективности и надежности сложных технических систем // Современные наукоемкие технологии. Региональное приложение. 2023. № 4. С. 60–68.
4. Афонин В. В., Никулин В. В. Оптимизация многоканальных систем массового обслуживания при больших загрузках // Вестник Астраханского государственного технического университета. Серия: Управление, вычислительная техника и информатика. 2020. № 3. С. 105–115.
5. Бобков С. П., Русанов К. И., Галиаскаров Э. Г. Сравнение аналитического и имитационного подходов к моделированию систем массового обслуживания // Сборник научных трудов ВУЗов России «Проблемы экономики, финансов и управления производством». 2022. № 50. С. 162–168.
6. Таратун В. Е., Шаперова В. С. Имитационное моделирование как подход в решении задач систем массового обслуживания // Системный анализ и логистика. 2020. № 4. С. 35–44.
7. Афонин В. В., Федосин С. А. Моделирование систем. М. : Лаборатория знаний, 2019. 231 c.
8. Исмаил А. И. М. Имитационное моделирование систем массового обслуживания // Apriori. Серия: Естественные и технические науки. 2016. № 2. С. 9.
Об авторах
А. А. БогнюковРоссия
студент
Д. Ю. Зорькин
Россия
преподаватель
Е. Г. Шведов
Россия
андидат физико-математических наук, доцент
Рецензия
Для цитирования:
Богнюков А.А., Зорькин Д.Ю., Шведов Е.Г. Имитационное моделирование и анализ систем массового обслуживания. Вестник кибернетики. 2025;24(1):53-59. https://doi.org/10.35266/1999-7604-2025-1-8
For citation:
Bognyukov A.A., Zorkin D.Yu., Shvedov E.G. Simulation modeling and analysis of queuing systems. Proceedings in Cybernetics. 2025;24(1):53-59. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-8















