Перейти к:
Компьютерное моделирование динамики численности популяций на основе модифицированной модели Лотки – Вольтерра
https://doi.org/10.35266/1999-7604-2025-1-9
Аннотация
Статья посвящена разработке модели динамики численности популяций на основе модели «хищник – жертва», учитывающей одновременное наличие в системе нескольких видов хищников и жертв, а также случайные изменения в количестве растительности за счет антропогенного воздействия и биотических факторов. Учет растительности как источника пищи для жертв хищников дополняет модель, делая ее более реалистичной и комплексной. Графики зависимости численности популяций от времени и фазовые портреты системы помогают в визуализации результатов моделирования и выявлении основных закономерностей. В целом разработка такой программы и использование ее в учебном процессе является отличным инструментом для обучения студентов, позволяя им применить теоретические знания на практике, провести анализ данных и сделать выводы о динамике популяций в экосистеме.
Ключевые слова
Для цитирования:
Никулин Р.Н., Авдеюк О.А. Компьютерное моделирование динамики численности популяций на основе модифицированной модели Лотки – Вольтерра. Вестник кибернетики. 2025;24(1):60-67. https://doi.org/10.35266/1999-7604-2025-1-9
For citation:
Nikulin R.N., Avdeyuk O.A. Computer modeling of population dynamics based on the modified Lotka–Volterra model. Proceedings in Cybernetics. 2025;24(1):60-67. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-9
ВВЕДЕНИЕ
Во многих случаях из-за невозможности прямого исследования реальных систем используют математическое моделирование и численную реализацию построенных моделей изучаемых процессов в виде компьютерных программ [1, 2]. Одной из таких задач является исследование динамики численности популяций животных.
Наиболее известной моделью «хищник – жертва» является модель, разработанная Лотки и Вольтерра и опубликованная в 1926 г. [3], которая в дальнейшем многократно корректировалась, и ее применение вышло далеко за рамки изначальной системы «хищник – жертва». Например, данная модель нашла применение в таких областях науки, как химия, физика плазмы, гидродинамика, экономика [4], а в работе [5] показана возможность использования рассматриваемой модели в политике и истории. Указанная модель изучается в вузовском курсе биофизики, включающем лабораторный практикум. Изучение динамики популяций на примере системы «хищник – жертва» целесообразно организовать в виде виртуальной лабораторной работы.
В настоящее время существуют программы, реализующие ту или иную модификацию модели «хищник – жертва». Например, в работе [6] приведена программа, реализованная в системе Matlab, но она неудобна для проведения лабораторной работы по дисциплине «Биофизика», так как студентам предлагается изменять параметры в тексте самой программы, для чего они должны обладать навыками работы в Matlab. Была предложена программа, реализующая простейшую модель «хищник – жертва», содержащую минимум параметров и пригодную только для первоначального ознакомления с рассматриваемой системой [7].
Практический интерес представляет разработка компьютерной программы на основании свободно распространяемого ПО, реализующей модель «хищник – жертва», учитывающей антропогенное и биотическое влияние на количество растительной пищи и имеющей простой и удобный интерфейс, позволяющий в течение лабораторного занятия ознакомиться с программой, выбрать необходимые параметры, провести моделирование и анализ результатов. Целью исследования является построение компьютерной программы, адаптированной для использования в учебном процессе в качестве виртуальной лабораторной работы и реализующей модель динамики численности популяций, которая учитывает взаимодействие более двух видов животных и ряд других параметров, повышающих адекватность модели.
МАТЕРИАЛЫ И МЕТОДЫ
Для построения математической модели обычно делают следующие предположения:
– пищевые ресурсы находятся в избытке, что позволяет иметь благоприятные условия для выживания и развития всех популяций;
– у популяций, имеющих достаточное количество пищи, прирост численности в единицу времени должен быть прямо пропорционален численности вида, помноженной на коэффициент рождаемости данной популяции;
– если среди индивидуумов различных популяций возникает борьба за пищевой ресурс, то его количество для каждой популяции будет зависеть от произведения числа особей на коэффициент, характеризующий межвидовую конкуренцию;
– количество погибших особей за выбранный период времени составляет определенную долю от численности популяции;
– если определенный пищевой ресурс ограничен и его используют несколько видов, то доля этого ресурса, используемая видом в единицу времени, равна произведению численности популяции этого вида на соответствующий коэффициент;
– в системе «хищник – жертва» рост численности популяции хищников напрямую зависит от вероятности встречи с представителями популяции их жертв.
В результате можно получить систему дифференциальных уравнений, описывающую поведение двух популяций (1):
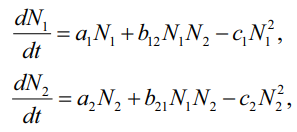 (1)
(1)
где N1, N1 – численности первой и второй популяций соответственно;
аi – коэффициенты собственных скоростей роста видов;
ci – константы самоограничения численности;
bij – константы взаимодействия видов [8].
В зависимости от значений b12 и b21 меняется тип взаимодействия видов между собой (индексы 1 и 2 относятся к разным видам).
Система дифференциальных уравнений, описывающая взаимодействие популяций типа «хищник – жертва» или «паразит – хозяин», имеет вид (2):
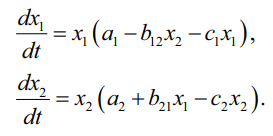 (2)
(2)
Вне зависимости от параметров системы в ее начале координат находится неустойчивый узел (3).
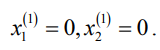 (3)
(3)
Кроме этого, существует три других потенциальных состояния равновесия (4)–(6):
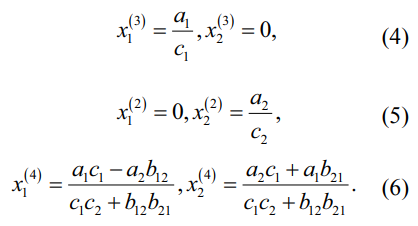
Уравнения (4)–(6) показывают, что в рассматриваемой системе возможны три случая:
– останется только популяция жертв (4);
– останется только популяция хищников (5);
– останутся обе популяции и будут сосуществовать вместе (6).
Рассмотрим третий случай, в котором популяции хищников и жертв устойчиво сосуществуют и их динамика определяется выражением (6).
Отметим, что сингулярная точка может проявляться как устойчивый узел или фокус – это зависит от соотношений параметров. Однако если в обоих уравнениях отсутствуют слагаемые, характеризующие процессы саморегуляции популяций (c1 = c2 = 0), то система уравнений (2) описывает модель Лотки – Вольтерра. Но если произойдет небольшое случайное отклонение, то эти колебания могут привести к полному вымиранию одного из видов.
Рассмотрим систему с неиссякаемым запасом растительности, который остается постоянным, что приводит безграничному увеличению популяции кроликов.
Кролики и растительность – это два ключевых фактора, определяющих бесконечное размножение кроликов. Взаимодействие между ними происходит спонтанно, что ведет к неограниченному росту популяции. Такая взаимосвязь является результатом второго закона термодинамики. Однако наличие лисиц (хищников) в такой системе влияет на характер изменения численности кроликов. Лисицы рассматривают кроликов как свою добычу и начинают охоту. Если растительности много, то возрастает число кроликов, что, в свою очередь, приводит к возрастанию численности лисиц.
С другой стороны, если учесть охоту человека на лисиц с целью добычи меха, то в данном случае лисицы выступают в роли жертв, подвергаясь истреблению или гибели по мере их размножения. Процесс охоты на лисиц можно считать способом вывода из системы энергии, тогда всю систему можно рассматривать как диссипативную структуру и описать ее системой дифференциальных уравнений. Описанный процесс имеет две стадии автокатализа с положительной обратной связью. Одна из них – «производство» кроликов, которые питаются растительностью.
Рассматриваемая система зависит от соотношения параметров и коэффициентов. При неправильно подобранных параметрах численность лисиц может оказаться настолько большой, что численность кроликов резко снизится и может достигнуть такого критического значения, после которого оно уже не восстановится, вследствие чего снизится и численность лисиц, которое также достигнет критического значения, ведущего к вымиранию популяции.
В природе такая структура имеет эффект диссипации, поэтому взаимодействие различных видов часто сопровождается циклическими колебаниями в численности популяций. Зная значения численности популяций в данный момент времени и используя рассматриваемую модель, можно предсказать эти значения в выбранный момент времени в будущем, так как изменения численности популяций носят периодический характер.
За основу возьмем систему дифференциальных уравнений, известную как модель Вольтерра для взаимодействия хищников и жертв. Ранее Лотка также применил подобную систему при изучении автокаталитических химических процессов. В связи с этим в литературе такая модель получила название модели Лотки – Вольтерра (7)–(8),
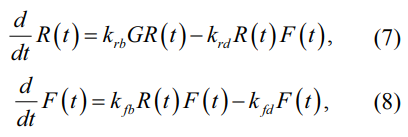
где krb – коэффициент рождаемости кроликов;
krd – коэффициент смертности кроликов;
kfb – коэффициент рождаемости лис;
kfd – коэффициент смертности лис в результате деятельности охотников.
Заметим сразу, что данная система обладает возможностью достижения устойчивого решения. Это означает, что при фиксированных материальных параметрах системы, которые не изменяются со временем, полностью определяются R0 и F0. Рассмотрим случай, когда производные в уравнениях (7) и (8) равняются нулю. Таким образом, можно разделить систему уравнений на два независимых уравнения и найти их решения (9)–(10):
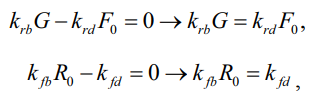 (9)
(9)
откуда:
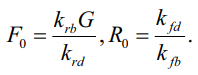 (10)
(10)
Отсюда видно, что популяция лисиц определяется исключительно параметрами кроликов, а популяция кроликов – параметрами лисиц, при этом неявно учитывается деятельность охотников.
В случае отклонения начальных параметров от установленных значений наблюдается колебательный процесс, в котором популяции периодически увеличиваются и уменьшаются в зависимости от коэффициентов и начальных параметров. В процессе охоты хищников на жертв количество последних сокращается, и когда оно достигает значения R0, численность хищников также начинает убывать вместе с уменьшением числа жертв. Сокращение численности жертв продолжается, пока количество хищников не достигнет значения F0, после чего начинает возрастать численность популяции жертв. В результате жертв становится достаточно для увеличения количества хищников и численность обоих популяций увеличивается, что приводит к повторению процесса.
Рассмотренная модель имеет несколько недостатков. С математической точки зрения система достаточно грубая, так как даже малейшие изменения хотя бы одного из коэффициентов приводят к значительным изменения в поведении системы, а с биологической – не учитывается насыщение, ограниченность ресурсов и другие факторы.
Таким образом, представленная модель, хотя и отражает взаимодействие между популяциями хищников и жертв, имеет свои ограничения как с точки зрения математики, так и с точки зрения биологии. Для полного понимания и адекватного описания рассматриваемой системы требуется учет дополнительных факторов и принципиальных свойств, характерных для таких взаимодействий.
Исходная модель «хищник – жертва» предполагает наличие только одного вида хищника и одного вида жертвы. Однако в реальности, в природе, существует множество различных видов как животных-хищников, так и жертв.
Поэтому предположим, что одновременное добавление нескольких видов жертв и хищников в исходную модель «хищник – жертва» может значительно усовершенствовать ее функционал и расширить возможности для исследования динамики популяций. Одной из таких возможностей является анализ взаимодействия различных видов хищников и жертв, а также факторов, влияющих на эти взаимодействия.
При построении более сложной модели, учитывающей одновременно несколько видов жертв и хищников, учтем, что лисицы помимо кроликов охотятся и на мышей, популяция которых M часто очень велика (11)–(14).
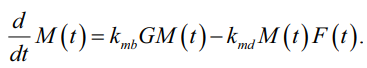 (11)
(11)
Здесь учтено, что увеличение численности мышей зависит от параметра G, который характеризует наличие растений, семенами которых они питаются. Теперь добавим в уравнение для популяции лисиц сумму (R+M), связанную с численностью двух видов жертв (кролики + мыши):
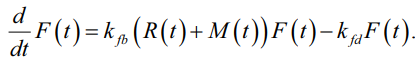 (12)
(12)
Добавим в систему еще одного хищника – популяцию сов O и соответствующее уравнение:
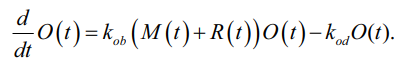 (13)
(13)
Для предотвращения неограниченного увеличения количества сов будем считать, что они сами является жертвой для других хищников (например, ястребов).
С учетом уравнений (11)–(13), система дифференциальных уравнений, описывающая взаимодействие указанных выше популяций, примет вид (14):
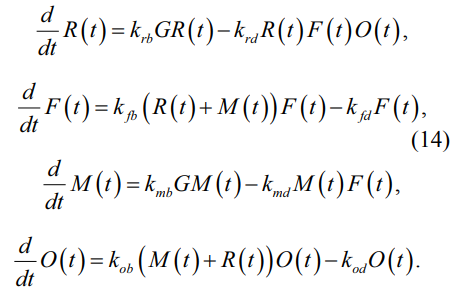
В исходной модели «хищник – жертва» не учитывается антропогенное и биотическое влияние на количество растительной пищи, которая важна для существования и развития травоядных, которые являются пищей (жертвами) для хищников. Деятельность человека приводит к изменению условий окружающей среды, что сказывается на наличии и количестве растительности, что напрямую влияет на численности и хищников, и их жертв.
Добавление случайных изменений в количестве травы, отражающее антропогенные и биотические факторы, усовершенствует модель «хищник – жертва», что позволяет более точно отражать сложную структуру экосистемы и корректно описывать биологические процессы [9, 10].
Для учета изменения среды вследствие антропогенных и абиотических факторов в первое и третье уравнения системы (14) необходимо добавить колебания параметра, характеризующего доступную растительность (15)–(16):
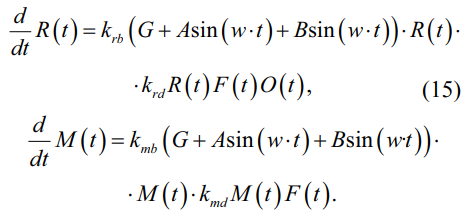
В результате система уравнений принимает окончательный вид:
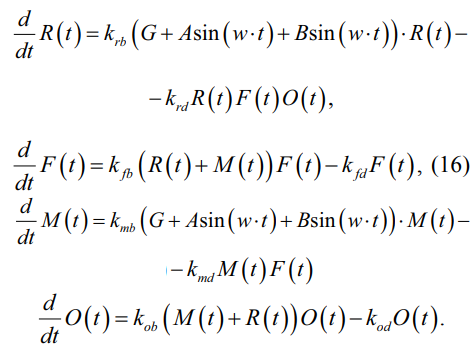
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Построенная модель позволяет установить связь между численностью популяций, коэффициентами их взаимодействия и начальными значениями популяций с учетом антропогенных и абиотических факторов и при их отсутствии, с помощью расчета изменения во времени численности рассматриваемых популяций и анализа фазовых портретов.
С целью реализации данной модели построена компьютерная программа с использованием языка Python и библиотек, необходимых для создания приложений [11–13], в которой для решения системы дифференциальных уравнений используется метод Рунге – Кутта четвертого порядка.
Скриншот окна программы с начальными параметрами приведен на рис. 1.
В качестве примера на рис. 2 приведен результат работы программы. В левой части рисунка – график изменения численностей популяций в зависимости от времени, а в правой – фазовый портрет системы.
Разработанная программа, кроме научных исследований, используется в учебном процессе в рамках изучения курса «Биофизика» в качестве компьютерной лабораторной работы.
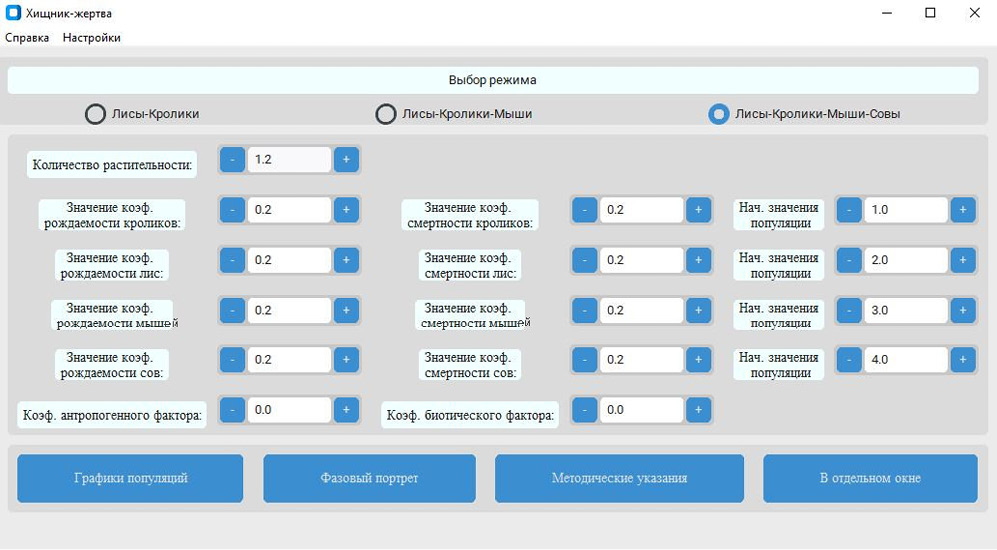
Рис. 1. Начальные параметры модифицированной модели «хищник – жертва»
Примечание: составлено авторами.
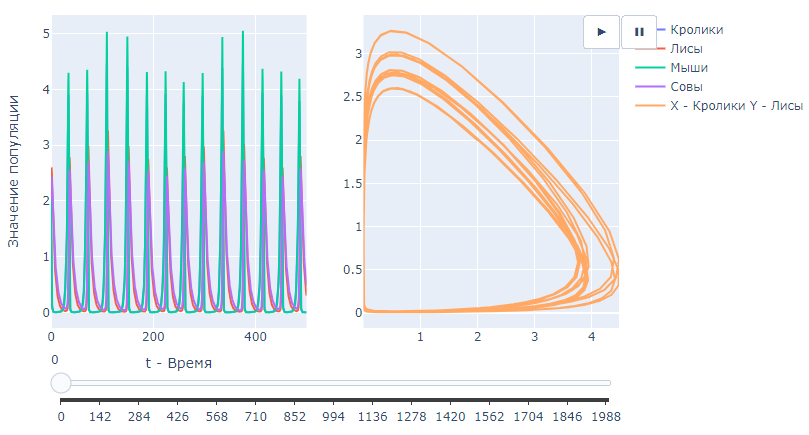
Рис. 2. Результаты моделирования
Примечание: составлено авторами.
ЗАКЛЮЧЕНИЕ
Исходя из модели Лотки – Вольтерра, была разработана модель динамики популяций, учитывающая взаимодействие нескольких видов животных, как, например, двух хищников и двух жертв. Эта модель также учитывает наличие растительности, которая является основным источником питания для жертв хищников в данном контексте. Для упрощения вычислений на основе этой модели была разработана компьютерная программа. Эта программа позволяет строить графики изменения численности популяций со временем и фазовые портреты системы на основе выбранных начальных данных. Она имеет интуитивно понятный интерфейс и предназначена для использования в учебных целях, в частности в лабораторных занятиях по дисциплине «Биофизика». Пользователи могут также ознакомиться с методическими рекомендациями, касающимися выполнения лабораторной работы по модели «хищник – жертва» внутри программы.
Список литературы
1. Никулин Р. Н., Шерстобитов С. О., Авдеюк О. А. и др. Компьютерное моделирование численности проточных и непроточных культур микроорганизмов // Инженерный вестник Дона. 2023. № 8. С. 650–658.
2. Никулин Р. Н., Никулина М. П., Грецова Н. В. и др. Моделирование биологических структур с помощью электрических эквивалентных схем замещения // Инженерный вестник Дона. 2020. № 2. С. 15.
3. Lotka A. J. Elements of physical biology. Baltimore: Williams & Wilkins, 1926. 495 p.
4. Diz-Pita E., Otero-Espinar M. V. Predator–Prey Models: A Review of Some Recent Advances // Mathematics. 2021. Vol. 9, no. 15. P. 1783. https://doi.org/10.3390/math9151783.
5. О возможности использования экологической модели в политике и в истории. URL: http://www.geokhi.ru/ DocNaturphilosophy /Analogies.pdf (дата обращения: 04.02.2025).
6. Лисы, Кролики, Мыши, Совы и Охотники. URL: http://www.geokhi.ru/DocNaturphilosophy/Bohr’s%20pair_3.pdf (дата обращения: 04.02.2025).
7. Казачков И. А., Гусева Е. Н. Компьютерная модель «Хищник-Жертва» // Современные научные исследования и инновации. 2017. № 1. С. 718–722.
8. Романовский Ю. М., Степанова Н. В., Чернавский Д. С. Математическое моделирование в биофизике. Москва – Ижевск : Институт компьютерных исследований, 2003. 402 c.
9. Тлегенов М. Т., Бекмуратов Б. М. Экологические особенности популяции Meriones tamariscinus в Низовьях Амударьи // Universum: химия и биология. 2022. № 3–1. С. 7–11.
10. Бекмуратова Д. М. Современное состояние вопроса влияния антропогенного воздействия на динамику численности млекопитающих Приаралья // Мировая наука. 2018. № 6. С. 137–140.
11. Barry Р. Head-first python: A Brain-Friendly Guide. California: O’reilly media, 2016. 624 p.
12. Rulta J. Python True Book. New York: However Publishing, 2021. 527 p.
13. Любанович Б. Простой Python. Современный стиль программирования. СПб. : Питер, 2016. 476 c.
Об авторах
Р. Н. НикулинРоссия
кандидат физико-математических наук, доцент
О. А. Авдеюк
Россия
кандидат технических наук, доцент, декан
Рецензия
Для цитирования:
Никулин Р.Н., Авдеюк О.А. Компьютерное моделирование динамики численности популяций на основе модифицированной модели Лотки – Вольтерра. Вестник кибернетики. 2025;24(1):60-67. https://doi.org/10.35266/1999-7604-2025-1-9
For citation:
Nikulin R.N., Avdeyuk O.A. Computer modeling of population dynamics based on the modified Lotka–Volterra model. Proceedings in Cybernetics. 2025;24(1):60-67. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-9















