Вычисление оценок параметров однородной вложенной кусочно-линейной регрессии с чередованием операций min и max

ВВЕДЕНИЕ

При анализе с помощью методов математического моделирования комплексных технических и социально-экономических объектов, исследователям приходится, наряду с линейными или сводящимся к линейным конструкциям, применять и весьма сложные, существенно нелинейные модельные формы. Так, в работе R. Neydorf математически обоснована возможность аппроксимационной мультипликативной и аддитивной обработки точечных экспериментальных данных для создания единой математической модели изучаемого объекта или явления в целом [1]. Предлагаемый метод называется аппроксимацией «Cut-glue», так как он основан на «разрезании» хорошо аппроксимируемых интервалов моделируемой зависимости и «склеивании» их в одну аналитическую функцию.

В работе Y. S. Lee и соавт. изучается динамика нелинейной системы с двумя степенями свободы, состоящей из заземленного линейного осциллятора, связанного с легкой массой посредством существенно нелинейной и нелинеаризуемой жесткости [2]. В статье A. V. Porubov и соавт. показано, что существенно нелинейные модели для твердых тел со сложной внутренней структурой могут быть изучены с использованием феноменологического и структурного подходов [3]. Установлено, что оба подхода приводят к одному и тому же нелинейному уравнению для бегущих продольных волн макродеформации.

Исследование T. C. Devezas и соавт. посвящено описанию новой кибернетической структуры, которая может помочь в понимании специфики своевременного развертывания повторяющихся социальных явлений, а также обеспечить основу для их применения в качестве полезных инструментов прогнозирования будущего [4]. H. Zhu и соавт. разработана новая многомерная математическая модель экономической системы с оператором опережения по времени τ и нелинейным фактором, отражающим учет ограниченной информации [5].

В статье M. E. Yahyaoui и соавт. представлена основанная на системе нелинейных дифференциальных уравнений новая математическая модель для управления циклической безработицей [6]. Производится классификация рабочей силы на три отдельных класса: принципиальные безработные, занятые лица и циклически безработные люди. В исследовании M. A. Misrol и соавт. на основе математической модели в виде задачи смешанного целочисленного нелинейного программирования изучается конфигурация нескольких систем возобновляемой энергии в экопромышленном парке, который генерирует электроэнергию для внутреннего потребления и экспортирует ее излишки в сеть [7].

В работе M. R. Khamiduulin и соавт. представлена экономико-математическая модель планирования производства, учитывающая его масштаб и выпуск бракованной продукции [8]. В статье A. H. Teru и соавт. предлагается и анализируется нелинейная математическая модель для изучения вырубки лесных ресурсов в условиях отсутствия четкой информации о полезности леса [9]. Модель имеет форму обыкновенных дифференциальных уравнений. Статья A. Aliyev посвящена анализу научных публикаций по созданию кусочно-линейных экономико-математических моделей в условиях неопределенности в конечномерном векторном пространстве [10].

Цель настоящей работы состоит в расширении класса так называемых вложенных кусочно-линейных регрессионных моделей путем рассмотрения зависимостей с чередованием операций min и max.

МАТЕРИАЛЫ И МЕТОДЫ

Пусть при анализе некоторого объекта исследователь полагает, что на зависимую (выходную) переменную y оказывают влияние m независимых (входных) переменных 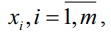 допуская тем самым наличие регрессионной связи 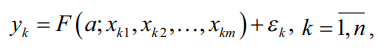(1),

(1)

где k – номер наблюдения, n – их число, а – вектор подлежащих определению параметров, F – вещественная, в общем случае нелинейная, аппроксимирующая функция, ε_k – ошибки аппроксимации. Будем считать все переменные в модели (1) детерминированными.

В работах [11, 12] одним из авторов предложено несколько форм вложенных кусочно-линейных регрессий, в частности:

– однородная вложенная кусочно-линейная регрессия первого типа (2)

е некоторого объекта исследователь полагает, что на зависиму

и

– однородная вложенная кусочно-линейная регрессия второго типа (3)

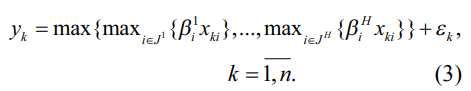
Здесь индексные множества 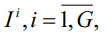 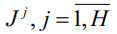представляют собой подмножества множества номеров независимых переменных {1, 2, …, m}. В том случае, когда вычисление оценок параметров вложенных кусочно-линейных регрессий производится путем минимизации сумм модулей ошибок аппроксимации:

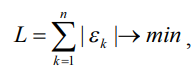
соответствующие задачи могут быть сведены (см, в частности, [13]) к задачам линейно-булева программирования (ЛБП).

По аналогии с вложенными формами (2) и (3) введем в рассмотрение однородные вложенные кусочно-линейные регрессии с чередованием операций min и max (4)–(5):

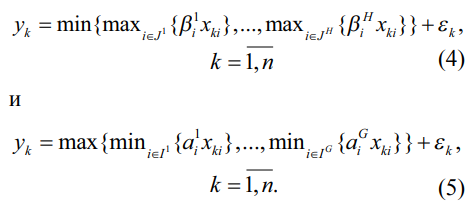
Используя вычислительный прием из работы [13], введем следующие обозначения:

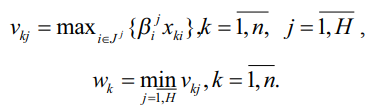
Тогда для вычисления оценок параметров регрессии (4) необходимо решить следующую задачу ЛБП (6)–(16):

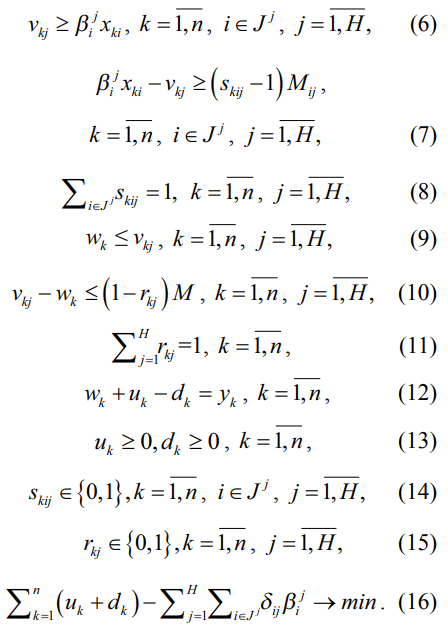
Здесь 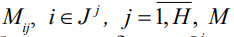 – наперед заданные большие, а 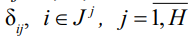,  – малые положительные числа.

Займемся теперь решением задачи идентификации параметров регрессии (5). Введем обозначения:

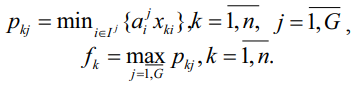
Тогда соответствующая задача ЛБП примет вид (17)–(27):

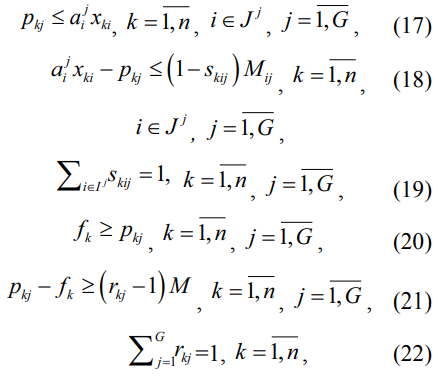
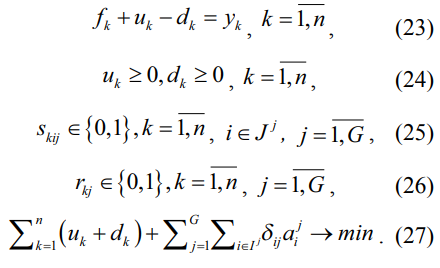
Здесь также 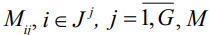 – наперед заданные большие, а 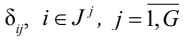,  – малые положительные числа.

Решение задач ЛБП (6)–(16) и (17)–(27) не должно вызывать вычислительных трудностей ввиду значительного количества соответствующих эффективных программных средств – например, популярная программа LPsolve (см, в частности, [14]).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Рассмотрим простой иллюстративный пример. Пусть исходная выборка данных имеет вид (таблица):

Таким образом, n = 6, m = 4.

Индексные множества J ¹ и J ² зададим в виде: J ¹ = {1,2}, J ² = {3,4}, т. е. положим H = 2.

Будем строить однородную вложенную кусочно-линейную регрессию с чередованием операций min и max (4) в форме:

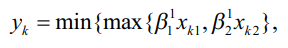
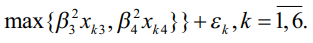
В результате решения задачи ЛБП (7)–(17) получим следующую модель 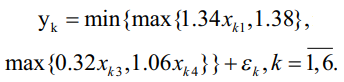(28):

 (28)

Приведем значения ключевых переменных задачи:

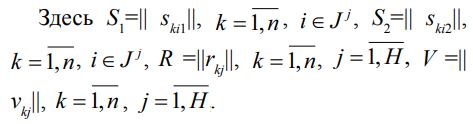
Анализ результирующих значений булевых переменных позволяет определить порядок срабатываний внешнего минимума и внутренних максимумов в модели (28). Например, в третьем наблюдении внешний минимум реализовался на первом внутреннем максимуме, который, в свою очередь, сработал на независимой переменной x₁.

ЗАКЛЮЧЕНИЕ

В работе введены однородные вложенные кусочно-линейные регрессии с чередованием операций min и max. Задачи идентификации их параметров путем минимизации сумм модулей ошибок аппроксимации сведены к задачам линейно-булева программирования. При этом значения булевых переменных позволяют установить порядок срабатывания внешнего минимума и внутренних максимумов в рассматриваемых вложенных моделях. Решен численный иллюстративный пример.