Перейти к:
О корреляционных и спектральных характеристиках кодов Баркера
https://doi.org/10.35266/1999-7604-2025-2-2
Аннотация
Исследование посвящено анализу автокорреляционных функций и спектров сигналов на основе бинарных и многофазных кодов Баркера. Цель работы – исследование влияния параметров последовательности и точности задания фаз на корреляционные и спектральные характеристики. Методология включает расчет нормированных автокорреляционных функций, оценку уровня боковых лепестков и спектральный анализ с учетом практических ограничений на фазовращатели. Показано, что многофазные коды Баркера имеют более сложную структуру автокорреляционных функций с нерегулярными боковыми лепестками по сравнению с бинарными кодами. При увеличении числа элементов спектр сигнала становится более нерегулярным, приближаясь к спектру одиночного радиоимпульса. Поскольку задание фазы с необходимой расчетной точностью практически нереализуемо, предложено использовать набор дискретных фазовращателей для сохранения приемлемых корреляционных свойств. Представлены рекомендации по выбору числа фазовращателей для достижения оптимальных характеристик. Научная новизна состоит в количественной оценке влияния квантования фазы на свойства многофазных кодов Баркера и практических рекомендациях по их реализации.
Ключевые слова
Для цитирования:
Дёмко А.И. О корреляционных и спектральных характеристиках кодов Баркера. Вестник кибернетики. 2025;24(2):14-22. https://doi.org/10.35266/1999-7604-2025-2-2
For citation:
Dyomko A.I. On correlation and spectral characteristics of Barker codes. Proceedings in Cybernetics. 2025;24(2):14-22. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-2
ВВЕДЕНИЕ
Развитие теории сигналов исторически тесно взаимосвязано с техникой их формирования и обработки. В последнее время важным фактором становится вычислительная часть, включающая в себя алгоритмы и возможности цифровых устройств. В связи с этим можно констатировать уменьшение появления новых сигналов, ориентированных на аналоговые способы формирования, и взрывной рост появления числа новых дискретно-кодированных сигналов. Сложные радиоимпульсные дискретно-кодированные сигналы могут иметь хорошие корреляционные свойства, определяемые структурой нулевого сечения функции неопределенности (ФН), автокорреляционной функцией (АКФ), при реализуемых высокостабильных схемах формирования и оптимальной обработки. Несмотря на многочисленные исследования в области сложных сигналов, дополнительные исследования в этой области имеют большое не только теоретическое, но и практическое значение.
МАТЕРИАЛЫ И МЕТОДЫ
Известны радиоимпульсные сигналы с нулевым уровнем боковых лепестков (УБЛ) нулевого сечения периодической функции неопределенности (ПФН) на основе кодов Фрэнка [1] и радиоимпульсных сигналов с квадратичным изменением начальных фаз [2]. В большинстве случаев на практике приходится иметь дело с сигналами и системами их обработки, в которых используется нулевое сечение функции неопределенности, которое для сложных сигналов имеет ненулевые боковые лепестки.
В источнике [3] обоснованы и введены усредненные параметры, характеризующие корреляционные свойства радиоимпульсных последовательностей из N радиоимпульсов, следующих с периодом Т:
1. Коэффициент оценки уровня боковых лепестков (1):
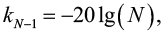 дБ, (1)
дБ, (1)
определяющий минимаксное значение УБЛ АКФ;
2. Коэффициент оптимальности (2):
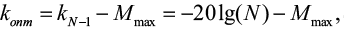 дБ, (2)
дБ, (2)
характеризующий степень превышения максимального УБЛ Mmax АКФ над потенциально достижимым.
В работе используются результаты моделирования и расчетов в программе MATLAB.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Известные коды Баркера [4] позволяют создавать дискретно-кодированные радиоимпульсные последовательности с постоянной величиной максимального бокового лепестка АКФ. Такие сигналы позиционируются как сигналы с идеальными корреляционными свойствами, для которых УБЛ АКФ совпадает с коэффициентом оценки УБЛ (1) при нулевом значении коэффициента оптимальности.
Первоначально были предложены бинарные коды Баркера [5] для последовательностей из 2, 3, 4, 5, 7, 11 и 13 элементов, причем для 2 и 4 элементов существуют по два варианта последовательностей. В дальнейшем разработаны [6], [7] и [8] многофазные коды Баркера из 6, 8, 9, 10, 12 и от 14 до 52 элементов, причем число различных последовательностей при фиксированном числе элементов достигает 3015.
Многофазные коды Баркера можно разделить на две категории:
– коды с ограниченным набором дискретных целочисленных значений фаз (3–5) в интервале от 0° до 360°;
– коды, для которых значения фазы не выбираются из ряда целочисленных значений и представляются вещественными числами с тремя знаками после запятой в интервале от 0° до 360°.
Для примера в табл. 1 приведены бинарные и многофазные коды Баркера для 13 и 14 элементов в последовательности.
Таблица 1
Значения фазы в соответствии с кодом Баркера
N/n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
13 | 0° | 0° | 0° | 0° | 0° | 180° | 180° |
13 | 0° | 0° | 180° | 180° | 60° | 60° | 120° |
14 | 0° | 0° | 1,709° | 286,585° | 347,346° | 128,366° | 90,757° |
Таблица 1. Продолжение
Значения фазы в соответствии с кодом Баркера
N/n | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
13 | 0° | 0° | 180° | 0° | 180° | 0° | |
13 | 60° | 60° | 180° | 0° | 240° | 0° | |
14 | 258,734° | 349,419° | 240,505° | 69,074° | 57,543° | 237,543° | 117,543° |
Примечание: составлено автором по [5] и [6].
В первой строке табл. 1 представлены значения фазы для бинарного кода Баркера из 13 элементов (два значения фазы: 0° и 180°). Во второй строке табл. 1 представлены значения фазы для многофазного кода Баркера из 13 элементов (пять значений фазы: 0°, 60°, 120°, 180° и 240°). В третьей строке табл. 1 представлены значения фазы для многофазного кода Баркера из 14 элементов (тринадцать значений фазы).
Существуют отличия кодов Баркера в структуре АКФ: для определенного числа элементов боковые лепестки имеют регулярную треугольную (рис. 1 и 2, первая строка табл. 1) форму (для числа элементов в последовательности 2, 3, 4, 5, 7, 11 и 13), а для других форма боковых лепестков нерегулярная (рис. 3, вторая и третья строки табл. 1).
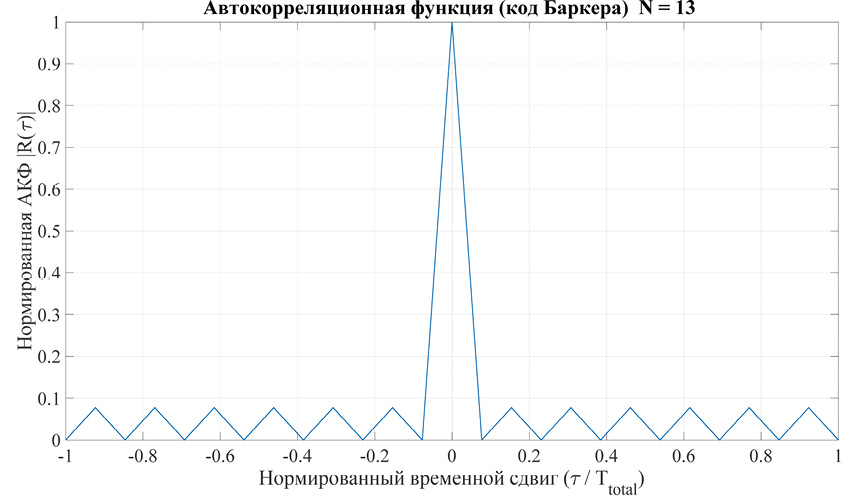
Рис. 1. Нормированная АКФ сигнала (13 элементов бинарного кода Баркера)
Примечание: составлено автором на основании данных, полученных в исследовании.
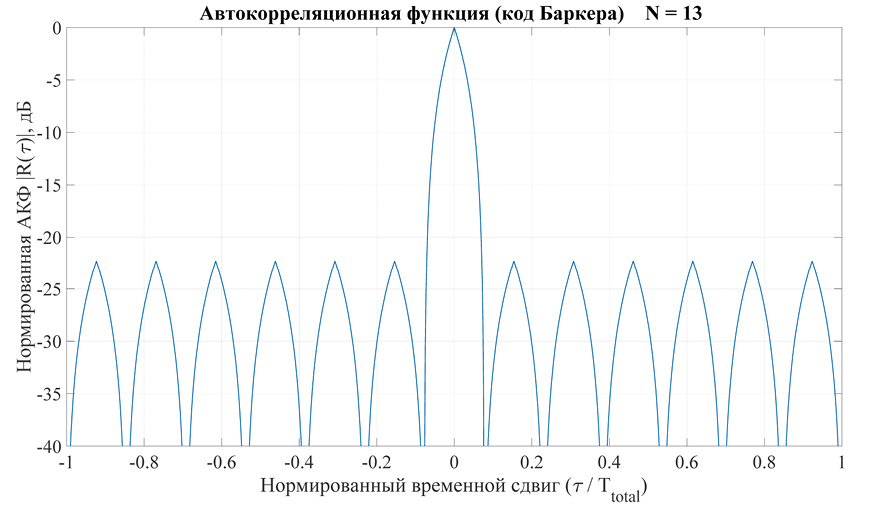
Рис. 2. Нормированная АКФ сигнала (13 элементов бинарного кода Баркера) в логарифмическом масштабе
Примечание: составлено автором на основании данных, полученных в исследовании.
Для удобства анализа и сравнения нормированная АКФ сигнала на основе бинарного кода Баркера из 13 элементов изображена в линейном (рис. 1) и логарифмическом (рис. 2) масштабах. АКФ состоит из области сильной корреляции (главного максимума) треугольной формы протяженностью 2τи по оси задержек и области слабой корреляции (боковых лепестков) при других значениях задержки.
УБЛ АКФ сигнала на основе бинарного кода Баркера из 13 элементов имеет постоянные не зависящие от задержки уровни максимальных значений (-22, 28 дБ), соответствующие (1).
Нормированная АКФ сигнала на основе многофазного кода Баркера (рис. 3) из 13 элементов имеет более сложную структуру боковых лепестков при постоянном максимальном значении боковых лепестков во всем интервале –22, 28 дБ.
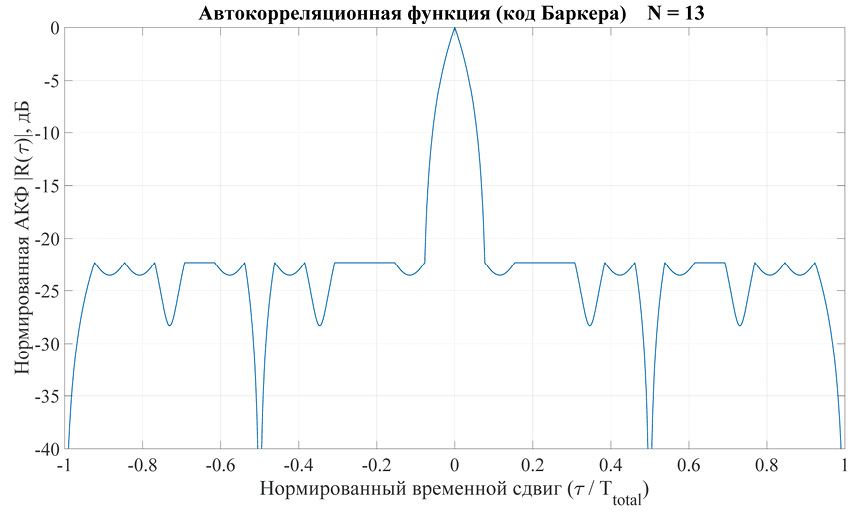
Рис. 3. Нормированная АКФ сигнала (13 элементов многофазного кода Баркера) в логарифмическом масштабе
Примечание: составлено автором на основании данных, полученных в исследовании.
На рис. 4 изображено сигнальное созвездие сигнала из 13 элементов многофазного кода Баркера, состоящее из пяти точек с поворотом на 60° между соседними значениями, причем пары точек расположены симметрично относительно друг друга (0° и 180°, 60° и 240°) со сдвигом 180°. При использовании дискретных цифровых фазовращателей [9] и [10] нужны будут лишь два фазовращателя (60° и 120°), поскольку для сигнала с нулевой фазой фазовращатель не требуется, сигнал с фазой 180° реализуется путем инвертирования сигнала с нулевой фазой, а сигнал с фазой 240° реализуется путем инвертирования сигнала с фазой 60°.
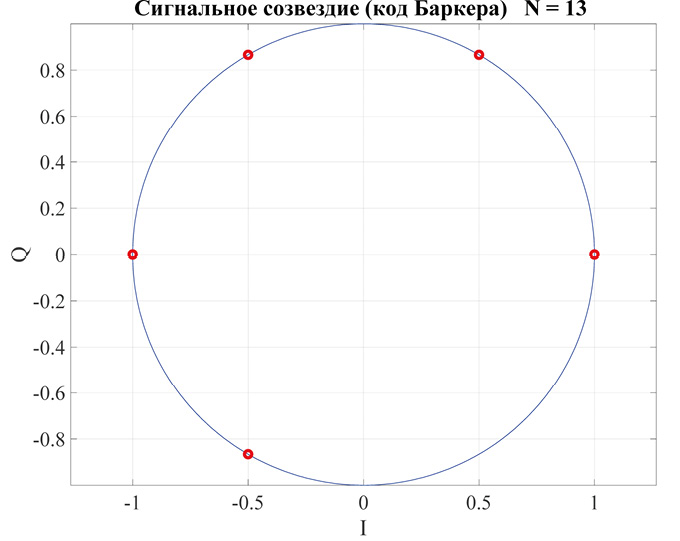
Рис. 4. Сигнальное созвездие сигнала (13 элементов многофазного кода Баркера)
Примечание: составлено автором на основании данных, полученных в исследовании.
На рис. 5 изображена нормированная АКФ многофазного кода Баркера для последовательности из 14 элементов.
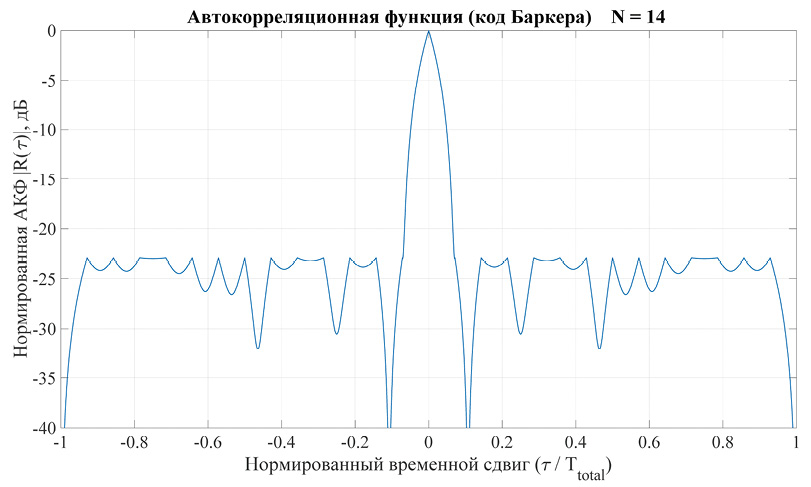
Рис. 5. Нормированная АКФ сигнала (14 элементов многофазного кода Баркера) в логарифмическом масштабе
Примечание: составлено автором на основании данных, полученных в исследовании.
Структура боковых лепестков такая же сложная, как и для многофазного кода Баркера для последовательности из 13 элементов, при постоянном максимальном значении УБЛ во всем интервале –22, 92 дБ, что также соответствует (1).
На рис. 6 изображено сигнальное созвездие сигнала на основе многофазного кода Баркера для последовательности из 14 элементов, состоящее из тринадцати точек, расположенных достаточно нерегулярно (в отличие от рис. 4) на окружности с неодинаковым поворотом между соседними значениями.
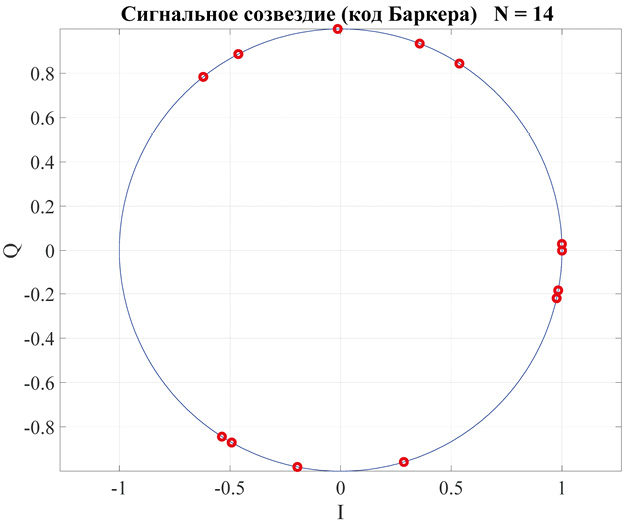
Рис. 6. Сигнальное созвездие сигнала (14 элементов многофазного кода Баркера)
Примечание: составлено автором на основании данных, полученных в исследовании.
Если оценить точность, с которой представлены в табл. 1 значения фазы для последовательности Баркера из 14 символов, то она составляет 0,00027 % (в предположении максимального значения фазы в 360°), что на практике реализовать невозможно для любых фазовращателей. Путем выполнения расчетов исследовано влияние точности задания фазовых сдвигов на корреляционные свойства рассматриваемых сигналов.
При отбрасывании дробных значений фазы структура АКФ почти не изменилась, УБЛ увеличился на 0,3 дБ, что несущественно.
Далее рассмотрено, сколько нужно дискретных фазовращателей, значения фазы которых отличаются в два раза (180°, 90°, 45°, 22,5°, 11,25°, 5,625°, 2,8125° и т. д.), чтобы обеспечить формирование сигнала на основе кода Баркера с заданной точностью. Установлено, что при использовании шести дискретных фазовращателей (минимальное значение фазового сдвига 5,625°) УБЛ возрастает на 2,18 дБ относительно расчетного (1), для семи фазовращателей (минимальное значение фазового сдвига 2,8125°) УБЛ возрастает на 0,64 дБ относительно расчетного, а для восьми фазовращателей (минимальное значение фазового сдвига 1,40625°) УБЛ возрастает на 0,58 дБ относительно расчетного. Отсюда следуют практические рекомендации (в зависимости от требований к УБЛ и разрядности памяти для хранения кодов фазы) по практическому использованию сигналов на основе кодов Баркера. При уменьшении числа дискретных фазовращателей сигнальное созвездие становится более регулярным.
На рис. 7 изображен спектр сигнала на основе бинарного кода Баркера из 13 элементов.
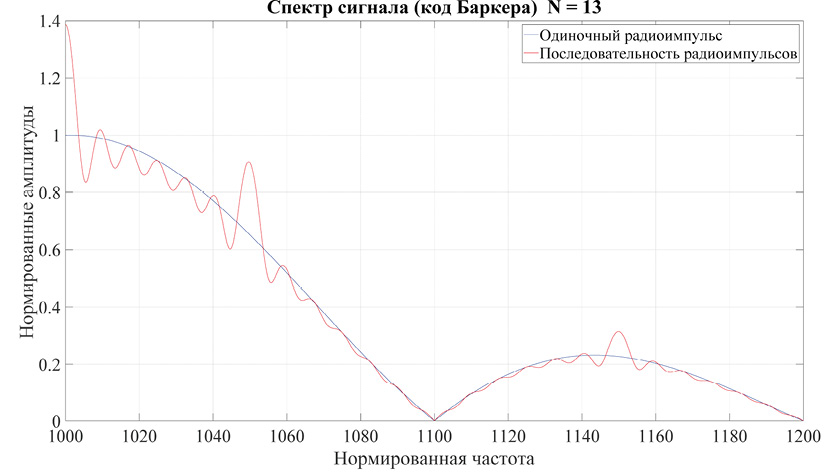
Рис. 7. Амплитудный спектр сигнала на основе бинарного кода Баркера для последовательности из 13 элементов
Примечание: составлено автором на основании данных, полученных в исследовании.
На рис. 8 изображен спектр сигнала на основе многофазного кода Баркера из 13 элементов.
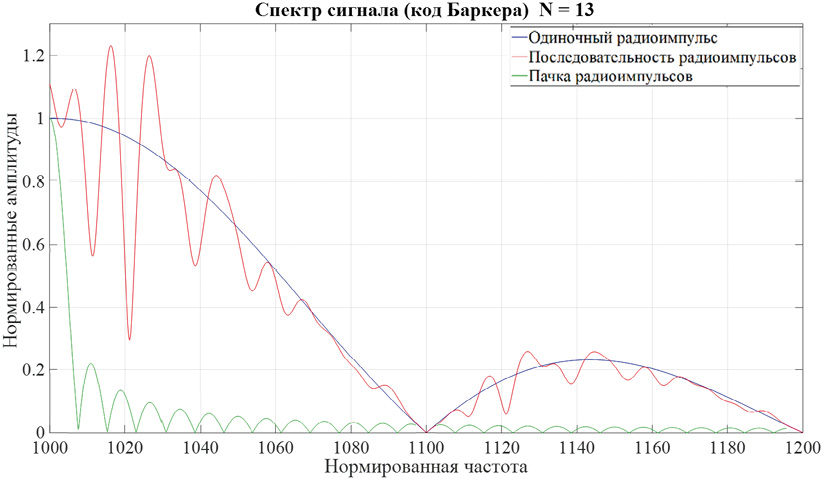
Рис. 8. Амплитудный спектр многофазного кода Баркера для последовательности из 13 элементов
Примечание: составлено автором на основании данных, полученных в исследовании.
На этом же рисунке приведен спектр одиночного импульса и спектр пачки из 13 радиоимпульсов с одинаковыми начальными фазами. Основная энергия спектральных составляющих сосредоточена в пределах участка, отстоящего от несущей частоты на обратную величину длительности радиоимпульса 1/τи. Спектр пачки радиоимпульсов намного сильнее сгруппирован около несущей частоты, что наглядно иллюстрирует сложный сигнал на основе кода Баркера: фазовая модуляция (изменение начальной фазы от импульса к импульсу) расширяет спектр по сравнению со спектром пачки радиоимпульсов.
Сравнение спектров фазоманипулированного (рис. 7) и многофазного (рис. 8) сигналов на основе кода Баркера для последовательности из 13 элементов показывает, что для сигнала с более регулярной структурой АКФ (рис. 1) огибающая спектра получается более регулярной (рис. 7).
На рис. 9 изображен спектр многофазного кода Баркера из 52 элементов. Огибающая спектра имеет нерегулярную структуру, в среднем приближаясь к огибающей одиночного радиоимпульса.
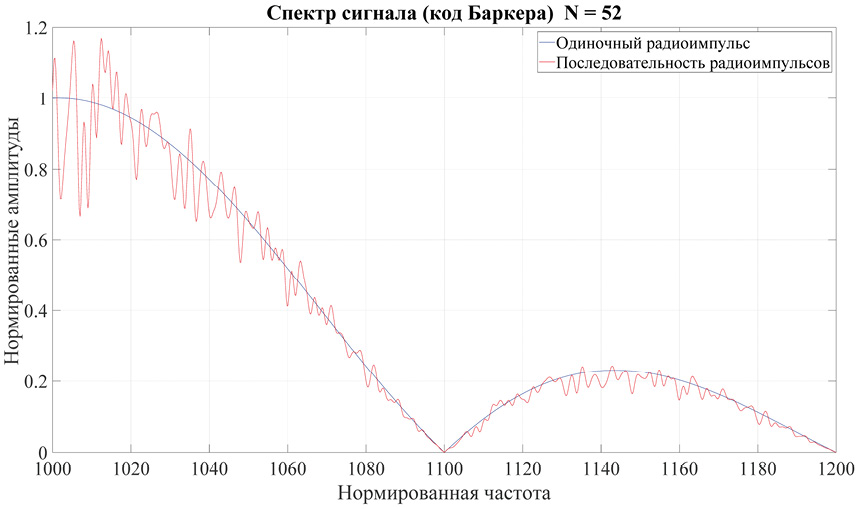
Рис. 9. Амплитудный спектр многофазного кода Баркера для последовательности из 52 элементов
Примечание: составлено автором на основании данных, полученных в исследовании.
С учетом сложного вида огибающей спектра сигнала на основе кода Баркера реализовать оптимальную обработку на основе согласованного фильтра для такого сигнала практически невозможно, следовательно, остается вариант корреляционной (одноканальной или многоканальной) обработки. При увеличении числа элементов в последовательности огибающая спектра сигнала на основе кода Баркера становится более нерегулярной, приближаясь к огибающей спектра одиночного радиоимпульса.
ЗАКЛЮЧЕНИЕ
Целью представленного исследования является анализ автокорреляционных функций и спектральных свойств кодов Баркера с акцентом на влияние длины последовательности и типа фазовых параметров на их корреляционные характеристики. Показано, что многофазные коды Баркера, хотя и имеют идеальные корреляционные свойства, очень сложны при практической реализации из-за высоких требований к точности задания фазовых сдвигов. Обоснована количественная оценка влияния квантования фазы на уровень боковых лепестков автокорреляционных функций и даны практические рекомендации по числу необходимых дискретных фазовращателей для достижения приемлемых характеристик. Данная работа восполняет существующий пробел между теоретическими свойствами кодов Баркера и ограничениями их практической реализации. Перспективным направлением дальнейших исследований является разработка схем фазовращателей с повышенной точностью для более полного использования идеальных свойств кодов Баркера в практических приложениях.
Список литературы
1. Фрэнк Р. Л. Многофазные коды с хорошими непериодическими корреляционными свойствами // Зарубежная радиоэлектроника. 1963. T. 17, № 12. С. 39–44.
2. Chu D. Polyphase codes with good periodic correlation properties // IEEE Transactions on Information Theory. Vol. 18, no. 4. P. 531–532. https://doi.org/10.1109/TIT.1972.1054840.
3. Дёмко А. И., Алмазова Е. Г. Оценка минимального достижимого уровня боковых лепестков функции неопределенности радиоимпульсных последовательностей // Вестник кибернетики. 2024. Т. 23, № 3. С. 96–102.
4. Дворников С. В., Дворников С. С., Марков Е. В. Модифицированные импульсные последовательности на основе кодов Баркера // Труды учебных заведений связи. 2022. Т. 8, № 1. С. 8–14.
5. Кук Ч., Бернфельд М. Радиолокационные сигналы. Теория и применение / пер. с англ. под ред. В. С. Кельзона. М. : Советское радио, 1971. 567 с.
6. Потехин Е. Н., Шувалов А. С., Леухин А. Н. Методы и результаты синтеза апериодических бинарных последовательностей и многофазных последовательностей Баркера // Цифровая Обработка Сигналов. 2013. № 4. С. 45–54.
7. Леухин А. Н., Парсаев Н. В. Бесконечные множества фазокодированных последовательностей с одноуровневой периодической автокорреляционной функцией // Радиотехника. 2009. № 12. С. 6–11.
8. Сьянов В. А. Подавление боковых лепестков составных фазокодомодулированных сигналов на основе кодов Баркера // Известия высших учебных заведений России. Радиоэлектроника. 2017. № 2. С. 53‒56.
9. Алмазова Е. Г., Дёмко А. И. Цифровые формирователи многофазных сигналов // Проблемы электроэнергетики и телекоммуникаций Севера России : сб. науч. тр. III Всерос. с междунар. уч. науч.-практ. конф., 21–22 апреля 2022 г., г. Сургут. М. : Знание-М, 2022. С. 414–419.
10. Дёмко А. И. Дискретный фазовращатель : патент № 225903 ; заявл. 02.08.2023 ; опубл. 13.05.2024. URL: https://patentimages.storage.googleapis.com/ab/ca/1d/6ec3be39120d21/RU225903U1.pdf (дата обращения: 17.03.2025).
Об авторе
А. И. ДёмкоРоссия
кандидат технических наук, доцент, почетный работник высшего образования РФ
Рецензия
Для цитирования:
Дёмко А.И. О корреляционных и спектральных характеристиках кодов Баркера. Вестник кибернетики. 2025;24(2):14-22. https://doi.org/10.35266/1999-7604-2025-2-2
For citation:
Dyomko A.I. On correlation and spectral characteristics of Barker codes. Proceedings in Cybernetics. 2025;24(2):14-22. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-2















