Перейти к:
Построение математической модели активной системы компенсации веса для проведения модальных испытаний слабодемпфированных аэрокосмических конструкций
https://doi.org/10.35266/1999-7604-2025-2-5
Аннотация
В настоящей работе описана математическая модель системы, способной компенсировать вес конструкции при проведении модальных испытаний. Данная модель включает в себя электротехническую и механическую подсистемы, поведение которых описывается вторым правилом Кирхгофа и вторым законом Ньютона соответственно. В среде Ansys Maxwell выполнено моделирование и расчет параметров постоянного магнита. Для экспериментального определения индуктивности катушки была собрана электрическая схема, а полученные данные аппроксимированы в программной среде MATLAB. В результате проведенного исследования сформирована система дифференциальных уравнений, описывающая динамику электромагнитной системы компенсации веса.
Ключевые слова
Для цитирования:
Максимов В.Н., Кондратьев К.В., Матюха Н.В., Максимов П.Н. Построение математической модели активной системы компенсации веса для проведения модальных испытаний слабодемпфированных аэрокосмических конструкций. Вестник кибернетики. 2025;24(2):38-46. https://doi.org/10.35266/1999-7604-2025-2-5
For citation:
Maksimov V.N., Kondratyev K.V., Matyukha N.V., Maksimov P.N. Mathematical model building of active weight compensation system for conducting modal tests of lightly damped aerospace structures. Proceedings in Cybernetics. 2025;24(2):38-46. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-5
ВВЕДЕНИЕ
Модальные испытания – это метод экспериментального исследования динамических характеристик механических систем. Основная цель таких испытаний – определение собственных частот, форм колебаний и коэффициентов демпфирования системы. Эти параметры важны для анализа динамического поведения объекта и его устойчивости к внешним воздействиям, например, вибрациям или ударам. При подготовке объекта к модальным испытаниям необходимо минимизировать нежелательные ограничения и демпфирования, а также исключить внешние воздействия, способные исказить результаты.
Одним из наиболее нежелательных внешних факторов при испытаниях аэрокосмической техники является влияние гравитации. Для исключения последней используются как пассивные, так и активные системы компенсации веса [1–4].
Пассивные системы компенсации веса работают без активного управления или внешнего источника энергии (например, электроприводов). Они используют механические свойства материалов и конструкций для уравновешивания веса объекта. Как правило пассивные системы строятся на пружинных или противовесных механизмах, которые имеют ряд минусов:
- Требуют точной предварительной настройки для конкретного веса.
- Пружинные системы могут иметь нелинейные характеристики, что приводит к неточной компенсации веса.
- Для тяжелых объектов механические пружины или противовесы могут стать громоздкими.
Для устранения данных недостатков используют активные системы компенсации веса.
В данной работе рассматривается электромагнитная система компенсации веса, изображенная на рис. 1.
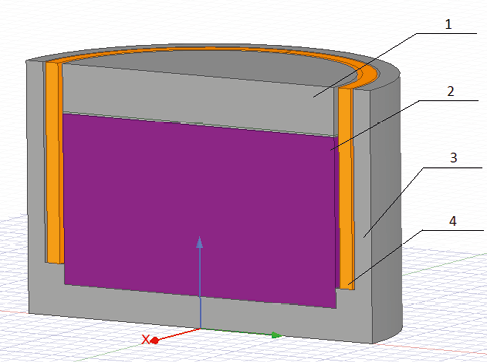
Рис. 1. Электромагнитная система
Примечание: составлено авторами.
Она включает в себя четыре основных элемента: магнитопроводы 1 и 3, изготовленные из электротехнической стали, мощный постоянный магнит 2, соленоид 4, представляющий собой медную обмотку из сплава M1. Функция постоянного магнита состоит в генерации магнитного поля, которое при взаимодействии с токами, протекающими в соленоиде, создает силу Ампера, выполняющую компенсирующую роль [5–7]. Поскольку вес конструкции компенсируется действием силы Ампера, необходимо, чтобы постоянный магнит создавал достаточно сильное магнитное поле, что позволяет избежать необходимости пропускания через соленоид токов большой величины при обезвешивании массивных объектов. В связи с этим в качестве постоянного магнита был выбран неодимовый магнит, обладающий остаточной магнитной индукцией, примерно втрое превышающей аналогичный параметр у ферритовых магнитов.
Работа системы основывается на электродинамических принципах взаимодействия проводника с магнитным полем. Ток, протекающий в соленоиде, при взаимодействии с магнитным полем в зазоре создает силу. Направление вектора силы определяется направлением тока. При протекании тока по часовой стрелке сила действует вертикально вверх, в противном случае – вертикально вниз. Данная сила способна компенсировать массу как соленоида, так и груза, который будет к нему прикреплен. Индуктивность соленоида в данной системе зависит от его положения. В случае если соленоид полностью в зазоре, его индуктивность максимальна и магнитное сопротивление системы минимально, в обратном случае индуктивность минимальна, а магнитное сопротивление системы максимально [8].
Для полного понимания работы данной системы необходимо получить математическую модель, представляющую собой систему из дифференциальных уравнений, которая способна в полной мере описать электродинамические принципы, обеспечивающие компенсацию веса соленоида и груза.
МАТЕРИАЛЫ И МЕТОДЫ
Математическая модель. Математическая модель включает в себя две взаимосвязанные подсистемы: механическую и электротехническую. Последняя из них по второму правилу Кирхгофа [9] является алгебраической суммой падения напряжения на активном сопротивлении системы, соленоиде и ЭДС самоиндукции, возникающей при движении соленоида:
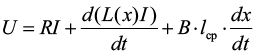 ,
,
где lср – усредненная длина одного витка соленоида, В – магнитная индукция неодимового магнита.
Если расписать производную произведения, уравнение, описывающее электротехническую подсистему, примет следующий вид:
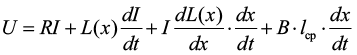 .
.
В целях упрощения записи при дальнейшем моделировании перепишем данное уравнение следующим образом:
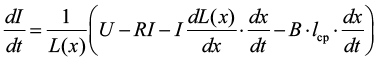 .
.
Подсистему, описывающую механическое взаимодействие элементов системы, можно записать как дифференциальное уравнение движения:
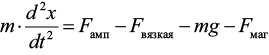 .
.
В данное уравнение входят четыре силы. Основными из них являются:
- Сила Ампера, перемещающая соленоид по вертикальной оси.
- Сила вязкого трения, пропорциональная скорости и описывающая сопротивление среды движению.
- Магнитная сила, являющаяся результатом взаимодействия магнитных индукций постоянного магнита и соленоида.
Расписав данные силы и записав все относительно ускорения системы, уравнение движения примет следующий вид:
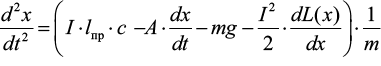 .
.
Для анализа величины B воспользуемся уравнением Максвелла о циркуляции магнитного поля [10], которое для постоянного магнита имеет следующий вид (1):
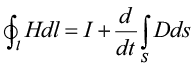 , (1)
, (1)
где D – электрическая индукция.
Через постоянный магнит не течет ток, следовательно, все, что находится в правой части уравнения (1), равно нулю. Таким образом, уравнение примет следующий вид:
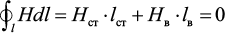 ,
,
где Hст и Hв – напряженности магнитного поля в стали и воздухе соответственно, lст и lв – участок циркуляции магнитного поля в стали:
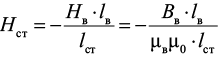 .
.
Ввиду высокой магнитной проницаемости стали вектор индукции внутри материала преимущественно ориентирован вдоль направления наименьшего магнитного сопротивления. Следовательно, при выходе в зазор, обладающий значительно меньшей магнитной проницаемостью, ориентация вектора не претерпевает изменений, оставаясь перпендикулярной поверхности границы. Таким образом, вектор не изменяется – Вст= Вв:
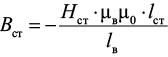 .
.
Для определения магнитной индукции в стали необходимо обратиться к петле гистерезиса, где отрицательной напряженности магнитного поля соответствует положительное значение индукции [11–13]. Этот подход позволяет учесть нелинейные свойства ферромагнитного материала и правильно интерпретировать его магнитное состояние.
Программный комплекс Ansys Maxwell оснащен встроенной библиотекой гистерезисных кривых для различных материалов, что позволяет учитывать их магнитные характеристики с высокой точностью. Благодаря этому в среде моделирования возможно воспроизвести поведение неодимового магнита и провести численный расчет создаваемой им магнитной индукции как в стальном магнитопроводе, учитывая сложные нелинейные зависимости материала, так и в воздушном зазоре.
На рис. 2 изображена расчетная модель, магнитная индукция в рабочей области воздушного зазора находится в диапазоне от 0,7908 до 0,6326.
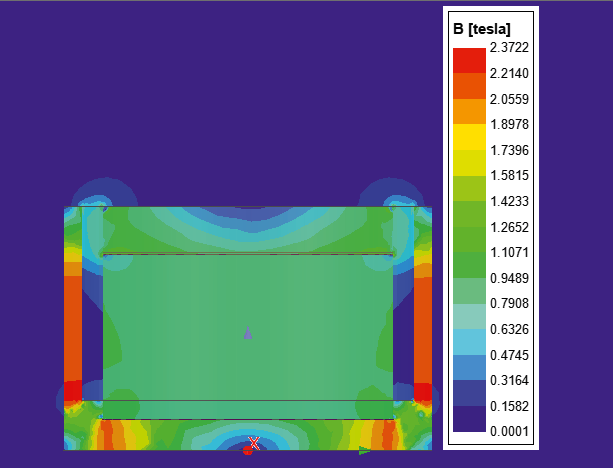
Рис. 2. Расчет постоянного магнита
Примечание: составлено авторами.
Для более точного расчета определения магнитной индукции определим магнитный поток, создаваемый магнитом. Для расчетной модели на рис. 2 он равен 0,031 Вб.
Отношением магнитного потока к площади сечения вычисляется магнитная индукция в зазоре:
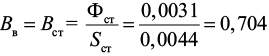 Tл.
Tл.
Для определения длины проволоки lпр воспользуемся следующим уравнением (2):
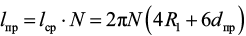 , (2)
, (2)
где R1 – радиус первого слоя обмотки, dпр – диаметр проволоки, N – число витков, пересекающих магнитный поток,
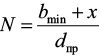 ,
,
где bmin – минимальная ширина катушки, пересекающая магнитный поток.
Как показано на рис. 3, основная часть магнитного потока сосредоточена в области зазора, однако некоторая его доля рассеивается за пределы зазора. В начальный момент времени катушка полностью размещена внутри зазора и, соответственно, пересекает только магнитный поток, сконцентрированный в нем. По мере выхода катушки за пределы зазора она начинает взаимодействовать с полным магнитным потоком, включая рассеянную его часть, вследствие чего увеличивается число витков, участвующих в работе обезвешивания.
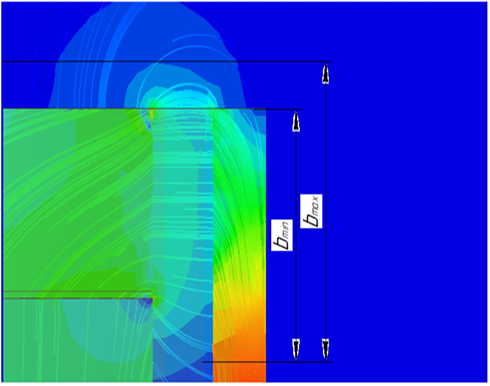
Рис. 3. Магнитное поле в зазоре
Примечание: составлено авторами.
Согласно рис. 3 можно определить максимальное число витков, пересекаемых магнитным потоком Фст:
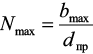 ,
,
где bmax – максимальная ширина катушки, пересекающая магнитный поток.
Следующим этапом определим индуктивность медной обмотки, которая представляет собой сложную нелинейную величину. Наличие данного факта делает аналитический расчет указанной величины весьма затруднительным, поэтому было принято решение провести экспериментальные замеры с последующим выведением эмпирической формулы. Для проведения измерений была составлена электрическая цепь, которая представлена на рис. 4.
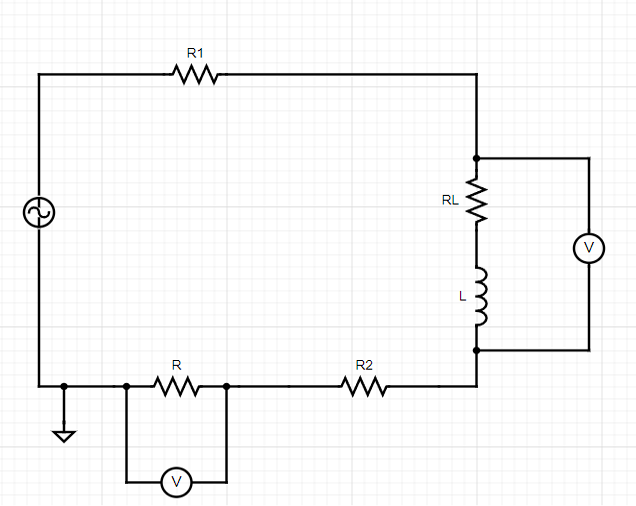
Рис. 4. Электрическая схема
Примечание: составлено авторами.
Данная цепь включает в себя источник переменного тока, сопротивления проводов R1 и R2, катушку индуктивности с индуктивностью L и активным сопротивлением RL, а также резистор с сопротивлением R.
Составленная электрическая схема позволяет замерить напряжения на резисторе и медной обмотке, которые, в свою очередь, выражаются следующими уравнениями:
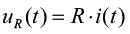 ,
,
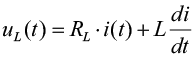 ,
,
где R – сопротивление резистора, RL – сопротивление медной обмотки, L – индуктивность медной обмотки.
Применив преобразование Фурье, получим следующие уравнения:
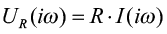 ,
,
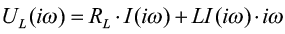 .
.
Данные зависимости позволяют составить следующую передаточную функцию:
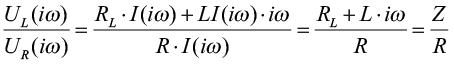 ,
,
где Z – импеданс медной обмотки.
Выведенная передаточная функция позволяет определить импеданс медной обмотки, что выражает ее полное сопротивление в области комплексных чисел, где реальная и мнимая части представляют собой активное и реактивное сопротивления медной обмотки соответственно:
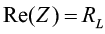 ,
,
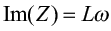 .
.
В итоге индуктивность можно получить, поделив мнимую часть импеданса на частоту ω.
Основной сложностью определения индуктивности медной обмотки является использование стального диска (рис. 1), поскольку он является областью индуцирования токов, оказывающего воздействие на внешнее магнитное поле, генерируемое соленоидом. Поэтому для проведения замеров была выбрана частота тока, подводимого к соленоиду, в 0,1 Гц.
Влияние изменения положения соленоида на его индуктивность демонстрируется на рис. 5.
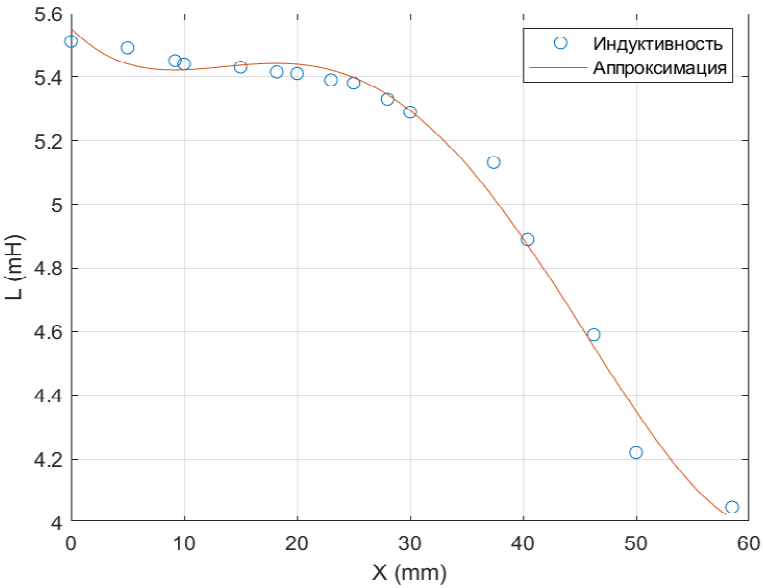
Рис. 5. Зависимость индуктивности от перемещения
Примечание: составлено авторами.
Учитывая нелинейное поведение индуктивности при изменении положения соленоида, для получения соответствующего уравнения была проведена полиномиальная аппроксимация (3):
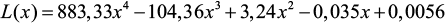 . (3)
. (3)
Продифференцировав данную функцию по перемещению, получим следующие уравнение (4):
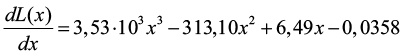 . (4)
. (4)
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В итоге электромагнитная система компенсации веса описывается двумя нелинейными дифференциальными уравнениями:
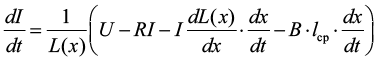 ,
,
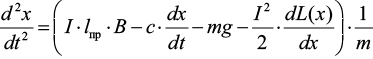 ,
,
в которых магнитная индукция постоянного магнита B, рассчитанная в программе Ansys Maxwell, равна 0,704 Тл, индуктивность катушки L (x) и ее производная по перемещению dL (x)/dx являются сложными функциями, которые были экспериментально замерены и аппроксимированы уравнениями (3) и (4) соответственно. Среднюю длину одного витка соленоида lср и длину проволоки, пересекающую магнитный поток lпр, можно найти из уравнения (2).
ЗАКЛЮЧЕНИЕ
Описанная математическая модель активной системы обезвешивания с использованием постоянного магнита и соленоида предназначена для компенсации веса при проведении модальных испытаний слабодемпфированных аэрокосмических конструкций. Определены характеристики постоянного магнита и получены зависимости индуктивности и ее производной от перемещения. Составлена система дифференциальных уравнений, включающая в себя механическую и электротехническую подсистемы. Полученные соотношения описывают поведение системы в зависимости от силы тока, подаваемого на медную обмотку, что позволяет провести компьютерное моделирование системы с использованием программного обеспечения MATLAB [14–20].
Список литературы
1. Иванов А. В., Зоммер С. А. Анализ процесса раскрытия зонтичного рефлектора на стенде с активной системой обезвешивания // Космические аппараты и технологии. 2021. Т. 5, № 4. С. 208–216.
2. Беляев А. С., Филипас А. А., Цавнин А. В. и др. Методика расчета системы обезвешивания крупногабаритных трансформируемых элементов космических аппаратов при наземных испытаниях // Сибирский аэрокосмический журнал. 2021. Т. 22, № 1. С. 106–120.
3. Беляев А. С., Филипас А. А., Курганов В. В. и др. Четырехтросовая система обезвешивания с управлением по вектору силы // Электротехнические и информационные комплексы и системы. 2022. Т. 18, № 2. С. 98–106.
4. Гайдукова А. О., Белянин Н. А. Обзор систем обезвешивания // Решетневские чтения. 2016. Т. 1. С. 93–95.
5. Schulte Westhoff B., Maas J. Design of an electromagnetic linear drive with permanent magnetic weight compensation // Actuators. 2024. Vol. 13, no. 3. P. 107. https://doi.org/10.3390/act13030107.
6. Janssen J. L. G., Paulides J. J. H., Lomonova E. A. et al. Design study on a magnetic gravity compensator with unequal magnet arrays // Mechatronics. 2013. Vol. 23. P. 197–203.
7. Pechhacker A., Wertjanz D., Csencsics E. et al. Integrated electromagnetic actuator with adaptable zero power gravity compensation // IEEE Transactions on Industrial Electronics. 2024. Vol. 71, no. 5. P. 5055–5062. https://doi.org/10.1109/TIE.2023.3288176.
8. Лысенков Я. А., Иванов Н. Н. Построение имитационной модели соленоида с использованием среды MATLAB Simulink // Вестник науки. 2023. Т. 4, № 5. С. 806–814.
9. Хоровиц П., Хилл У., Искусство схемотехники; в 3-х т. 4-е изд., перераб. и доп. / пер. с англ. Бронина Б. Н., Коротова А. И., Микшиса М. Н. и др. М. : Мир, 1993. Т. 1. 413 с.
10. Parker R. J. Advances in Permanent Magnetism. New York: By John Wiley & Sons, 1990. 352 p.
11. Монк С., Шерц П. Электроника. Теория и практика : практич. руководство. СПб. : БХВ-Петербург, 2018. 1168 с.
12. Альтман А. Б., Верниковский Э. Е., Герберг А. Н. и др. Постоянные магниты. Справочник. 2-е изд. перераб., доп. М. : Энергия, 1980. 488 с.
13. Арнольд Р. Р. Расчет и проектирование магнитных систем с постоянными магнитами. М. : Энергия, 1969. 184 с.
14. Brezak D., Kovač A., Firak M. MATLAB/Simulink simulation of low-pressure PEM electrolyzer stack // International Journal of Hydrogen Energy. 2023. Vol. 48, no. 16. P. 6158–6173. https://doi.org/10.1016/j.ijhydene.2022.03.092.
15. Taha Z., Aydın K., Arafah D. et al. Comparative simulation analysis of electric vehicle powertrains with different configurations using AVL cruise and MATLABSimulink // New Energy Exploitation and Application. 2024. Vol. 3, no. 1. P. 171–184. https://doi.org/10.54963/neea.v3i1.276.
16. Naz F. Closed loop buck & boost converter mathematical modeling, analysis and simulation using MATLAB // International Journal of Engineering and Advanced Technology (IJEAT). 2021. Vol. 10, no. 4. P. 263–271. https://doi.org/10.35940/ijeat.D2525.0410421.
17. Красинский А. Я., Ильина А. Н., Красинская Э. М. и др. Математическое и компьютерное моделирование динамики планетохода с радиально деформируемыми колесами // Труды МАИ. 2017. № 95. С. 30.
18. Гавва Л. М. Параметрический анализ в операционной среде MATLAB напряжённо-деформированного состояния конструктивно-анизотропных панелей из композиционных материалов с учётом технологии изготовления // Труды МАИ. 2017. № 93. С. 27.
19. Фaдин Д. А. Использование среды MATLABSimulink для реализации вычислительных алгоритмов в целочисленных микропроцессорных системах // Труды МАИ. 2015. № 80. С. 22.
20. Абдали Л. М. А., Аль-Малики М. Н. К., Кувшинов В. В. и др. Математическое моделирование с использованием алгоритма контроля точки максимальной мощности для фотоэлектрической системы // Труды МАИ. 2023. № 130. С. 20.
Об авторах
В. Н. МаксимовРоссия
аспирант, инженер
К. В. Кондратьев
Россия
кандидат технических наук, начальник группы отработки новых методов испытаний
Н. В. Матюха
Россия
ведущий инженер
П. Н. Максимов
Россия
аспирант, инженер
Рецензия
Для цитирования:
Максимов В.Н., Кондратьев К.В., Матюха Н.В., Максимов П.Н. Построение математической модели активной системы компенсации веса для проведения модальных испытаний слабодемпфированных аэрокосмических конструкций. Вестник кибернетики. 2025;24(2):38-46. https://doi.org/10.35266/1999-7604-2025-2-5
For citation:
Maksimov V.N., Kondratyev K.V., Matyukha N.V., Maksimov P.N. Mathematical model building of active weight compensation system for conducting modal tests of lightly damped aerospace structures. Proceedings in Cybernetics. 2025;24(2):38-46. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-5















