Перейти к:
Анализ обеспечения целостности сигнала на печатной плате при проектировании высокопроизводительных вычислительных устройств
https://doi.org/10.35266/1999-7604-2025-2-6
Аннотация
Проведен всесторонний анализ перекрестных помех между различными микрополосковыми структурами на печатных платах. В качестве метода анализа использовался метод конечных разностей во временной области, обеспечивающий точное моделирование распространения электромагнитных волн и, как следствие, перекрестных помех. Диапазон частот, охваченный моделированием, составлял до 10 ГГц. Этот широкий диапазон критически важен для оценки влияния перекрестных помех на высокоскоростные цифровые и аналоговые схемы, где паразитные эффекты могут существенно влиять на производительность. Моделирование показало, что микрополосковые линии с двойным выступом снижают перекрестные помехи на дальнем конце более чем на 35 % по сравнению с параллельными линиями, но при этом увеличивают перекрестные помехи на ближнем конце более чем на 12 %. Линии с чередующимися выступами показали хорошие результаты в снижении на дальнем конце. Параллельные змеевидные микрополосковые линии уменьшили на дальнем конце более чем на 10 дБ и на ближнем конце примерно на 2 дБ, чем другие структуры. На основе параметров индуктивности и емкости проанализированы вносимые потери (100 МГц – 20 ГГц), на ближнем конце, собственное сопротивление в частотной и передача во временной области, с последующим сравнением трассировок с выступами и без них. Разработан метод моделирования эквивалентной схемы трассировки с трапециевидными отрезками, основанный на сегментации. Предложенная модель верифицирована посредством 3D-электромагнитного моделирования и измерений в частотной области.
Ключевые слова
Для цитирования:
Пирогов А.А., Хорошайлова М.В., Назаренко Н.Г., Сёмка Э.В. Анализ обеспечения целостности сигнала на печатной плате при проектировании высокопроизводительных вычислительных устройств. Вестник кибернетики. 2025;24(2):47-57. https://doi.org/10.35266/1999-7604-2025-2-6
For citation:
Pirogov A.A., Khoroshailova M.V., Nazarenko N.G., Syomka E.V. Signal integrity control analysis on printed circuit board in design of high-performance computing devices. Proceedings in Cybernetics. 2025;24(2):47-57. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-6
ВВЕДЕНИЕ
Современные печатные платы сталкиваются с вызовами в области целостности сигналов, что требует применения специализированных методов компоновки и трассировки. Основная задача заключается в минимизации искажений сигнала при его передаче от источника к приемнику.
Для достижения этой цели применяются ключевые стратегии, включая разработку многослойной структуры, которая включает оптимизацию распределения питания, заземляющих проводников и сигнальных цепей. Кроме того, важной является грамотная подборка компонентов, что включает выбор конденсаторов, расчет импеданса, а также учет ограничений для цепей и дифференциальных пар.
При работе с высокоскоростными сигналами критически важно точно рассчитать импеданс для предотвращения отражений, снижения потерь и дисперсии, устранения перекрестных помех, минимизации излучательных потерь и обеспечения корректного уровня цифровых сигналов. Необходимо также учитывать влияние высокочастотных эффектов, вызванных паразитными компонентами и потерями, обусловленными шероховатостью меди.
Надежное заземление и его правильное размещение вблизи сигнальных проводников играют ключевую роль. Правильная организация слоев и оптимальный выбор конфигурации слоев питания и заземления позволяют эффективно решать множество проблем, связанных с электромагнитной совместимостью и целостностью передаваемых сигналов.
Обеспечение целостности сигнала (ЦС) на печатной плате (ПП) критически важно для проектирования высокопроизводительных вычислительных устройств. С ростом частот и плотности компонентов, проблемы, такие как отражения, перекрестные помехи и потери мощности, оказывают существенное влияние на функциональность и надежность системы.
Анализ ЦС включает моделирование поведения сигналов, используя такие методы, как анализ во временной и частотной областях. Необходимо учитывать импеданс трасс, согласование нагрузок, развязку питания и заземления. Особое внимание уделяется проектированию дифференциальных пар, расположению компонентов и выбору материалов ПП с низкими диэлектрическими потерями.
Для минимизации проблем ЦС используются специализированные программные средства для моделирования и верификации. Валидация физического прототипа с помощью измерений параметров S-параметров, временной области (ВО) и анализа электрического поля подтверждает соответствие требованиям. Правильный анализ и проектирование ЦС гарантируют оптимальную производительность и надежность вычислительного устройства.
МАТЕРИАЛЫ И МЕТОДЫ
Моделирование перекрестных помех (Crosstalk) на ближнем конце NEXT (Near-End Crosstalk) и дальнем конце FEXT (Far-End Crosstalk) на печатной плате (ПП) является критически важным этапом при проектировании высокопроизводительных вычислительных устройств. Метод конечных разностей во временной области (КРВО) предоставляет эффективный инструмент для анализа и уменьшения этих помех. В процессе моделирования учитываются геометрия проводников, диэлектрические свойства материала ПП и характеристики сигналов [1–3].
Применение КРВО позволяет точно оценить амплитуду и форму импульсов NEXT и FEXT, возникающих из-за емкостной и индуктивной связи между линиями передачи. Результаты моделирования используются для оптимизации трассировки, добавления экранирующих слоев и подбора импеданса с целью минимизации перекрестных помех и обеспечения целостности сигнала. Валидация модели КРВО осуществляется путем сравнения результатов симуляции с измерениями на тестовых платах. Снижение уровня перекрестных помех улучшает производительность и надежность вычислительных устройств.
На рис. 1 представлены параллельные микрополосковые линии на печатной плате. В данном случае первая линия функционирует как источник помех (агрессор), а вторая линия подвергается воздействию этих помех (жертва), на которой возникают перекрестные интерференции.

Рис. 1. Параллельные линии проводников на печатной плате
Примечание: составлено авторами.
В описанных линиях источник сигнала находится на одном конце агрессора, в то время как его противоположный конец соединен с нагрузкой модулем 50 Ом. Перекрестные помехи NEXT и FEXT можно представить в виде различных индуктивных и емкостных связей.
Рис. 2 демонстрирует дорожки на печатных платах, одна сторона микрополосковой линии которой касается воздуха.
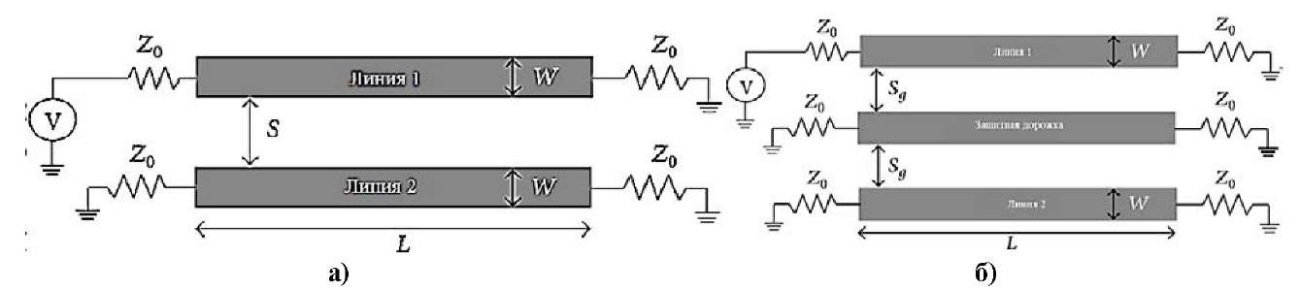
Рис. 2. Дорожки на печатных платах: а) параллельные линии проводников на печатной плате; б) линии проводников на печатной плате с защитной дорожкой
Примечание: составлено авторами.
На диэлектрическом слое формируются дорожки, а заземление располагается на нижней стороне этого слоя. Линии имеют одинаковую ширину (W) и равную длину (L), при этом подложка характеризуется диэлектрической проницаемостью εr и толщиной H, а проводник – толщиной t и шириной W. Расстояние между линиями обозначается буквой S.
На рис. 2а представлены стандартные параллельные микрополоски, расположенные с интервалом S, при этом индуктивная связь между ними значительно превышает емкостную. Один из способов уменьшить перекрестные помехи – увеличить расстояние между линиями агрессора и жертвы, но это снижает плотность упаковки. Другой метод – вставка защитной трассы между этими линиями на расстоянии Sg (рис. 2б), что помогает уменьшить помехи. Защитная трасса имеет те же размеры, что и линии агрессора и жертвы, чтобы минимизировать сложности, однако может привести к несбалансированности импеданса. Альтернативным решением может быть использование сквозной защитной трассировки, но это не всегда подходит при общей плате.
Чередующаяся микрополосковая линия представляет собой альтернативную маршрутизацию для снижения перекрестных помех, где трассы приближены к пропорциональным линиям, что видно на рис. 3а. На рис. 3б представлена микрополосковая линия с переменными выступами, прикрепленными вертикально как к линиям агрессора, так и к линиям жертвы.
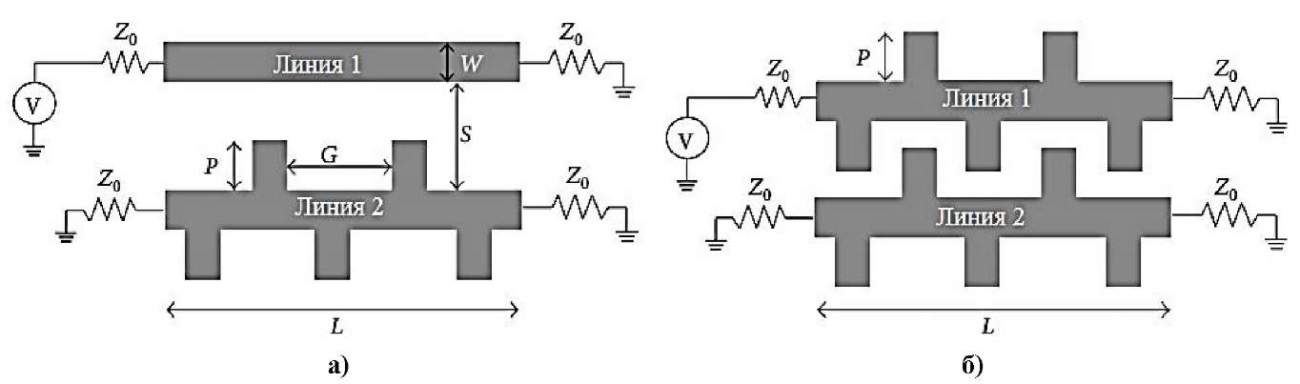
Рис. 3. Микрополосковая линия с переменными выступами: а) конфигурация с одним выступом; б) конфигурация с двойным выступом
Примечание: составлено авторами.
Использование КРВО открывает возможности для решения электромагнитных задач в одномерных, двумерных и трехмерных пространствах. Этот подход основан на модифицированных уравнениях Максвелла, применяемых с центральными разностями для получения приближенных решений.
В отличие от частотной области, где уравнения Максвелла решаются для конкретных частот, КРВО решает их непосредственно во временной области, предоставляя решения, изменяющиеся во времени, для электромагнитных полей. Этот подход особенно полезен для анализа широкополосных сигналов и переходных процессов, когда частотный анализ может быть громоздким.
Ключевыми уравнениями, используемыми в методе КРВО, являются закон Ампера и закон Фарадея, представленные в дифференциальной форме. Эти уравнения устанавливают взаимосвязь между изменениями электрического поля и магнитного поля и наоборот. В КРВО пространство и время дискретизируются, что позволяет заменить дифференциальные операторы на централизованные разностные аппроксимации, тем самым обеспечивая численное решение уравнений Максвелла.
Приведенные ниже уравнения Максвелла применяются для анализа электрических и магнитных полей во временной области (1)–(3):
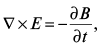 (1)
(1)
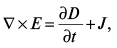 (2)
(2)
где D – напряженность электрического поля, а B – плотность магнитного потока, которые могут быть записаны через E и H как
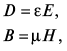 (3)
(3)
где μ обозначает проницаемость, а ε – диэлектрическую проницаемость. Структура предполагалась без потерь, среда изотропная и однородная.
Эта дискретизация приводит к набору алгебраических уравнений, которые могут быть решены итеративно для вычисления значений электрического и магнитного полей в каждой точке сетки в каждый момент времени. Для обеспечения точности и стабильности решения необходимо соблюдать критерий Куранта – Фридрихса – Леви (CFL), который связывает размер шага по времени с размером ячейки сетки.
На рис. 4 представлена система передачи данных в запоминающем устройстве, которая состоит из центрального процессора (ЦП), ПП и двойного модуля памяти (DIMM). В этом контексте особое внимание уделяется ключевым аспектам ЦС.
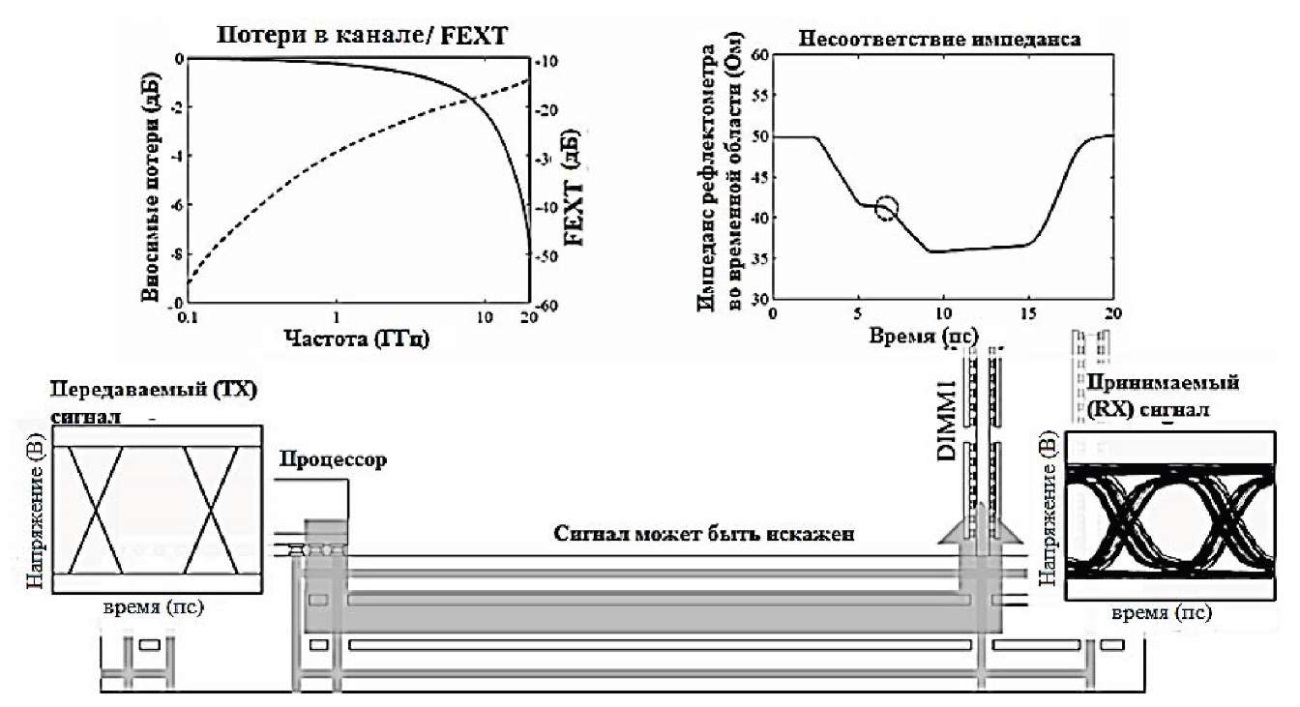
Рис. 4. Нарушение целостности пути передачи сигнала в запоминающем устройстве
Примечание: составлено авторами.
В этой системе возникают проблемы с ЦС в высокоскоростном канале передачи данных, которые обусловлены потерями в канале, пересечениями на дальних границах и несовпадением импедансов. Проектирование таких каналов должно принимать во внимание указанные недостатки. Для увеличения скорости передачи в системе памяти необходимо уменьшить задержку в высокоскоростном канале. Кроме того, важно контролировать рефлектометрию во ВО и снизить потери, а также FEXT. В ограниченном пространстве высокая плотность каналов вызывает ухудшение передачи данных. В контексте высокопроизводительных серверных плат, используется конструкция трассировки, известная как tabbed routing, которая представляет собой эффективный метод для оптимизации целостности сигнала. Tabbed routing использует стратегическое размещение проводников, создавая своего рода «вкладки» или ответвления вдоль основной трассы, при таком методе трассировки проводники располагаются слоями и соединяются между собой через межслойные переходы (виа). Это позволяет более эффективно использовать доступное пространство платы, уменьшить перекрестные помехи и минимизировать длину трасс, что критически важно для высокоскоростных сигналов [4].
Ключевым элементом этой конструкции является применение усеченных трапециевидных отрезков. Эти усеченные отрезки выполняют двойную функцию: во-первых, они минимизируют FEXT, эффективно подавляя нежелательные электромагнитные помехи между соседними сигналами. Во-вторых, усеченные трапециевидные отрезки способствуют стабилизации импеданса трассы. Контролируемый импеданс критически важен для предотвращения отражений сигнала, которые могут привести к искажениям и снижению производительности.
В совокупности tabbed routing с использованием усеченных трапециевидных отрезков обеспечивает более чистый и стабильный путь сигнала, что особенно важно в средах, где скорость и надежность передачи данных имеют первостепенное значение.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В табл. 1 указаны параметры структуры и их определения.
Таблица 1
Структурные параметры, используемые при проектировании высокоскоростного канала передачи сигналов с использованием усеченных трапециевидных отрезков
Параметр | Определение |
wchannel | Ширина канала без выступа |
schannel | Расстояние между каналами |
lwtab | Длинная ширина на выступе |
swtab | Короткая ширина на выступе |
ltab | Длина выступа |
stab | Расстояние между выступами |
Примечание: составлено авторами.
Рис. 5а демонстрирует верхний и боковой виды маршрутизации с одним блоком трапециевидных отрезков. На рис. 5б в сегментах А и Б ширина канала может варьироваться из-за конструктивных особенностей трапециевидного выступа. В отличие от стандартной линии передачи, маршрутизация с выступами требует моделирования с использованием одноэлементного выступа для оптимального сохранения сигнала.
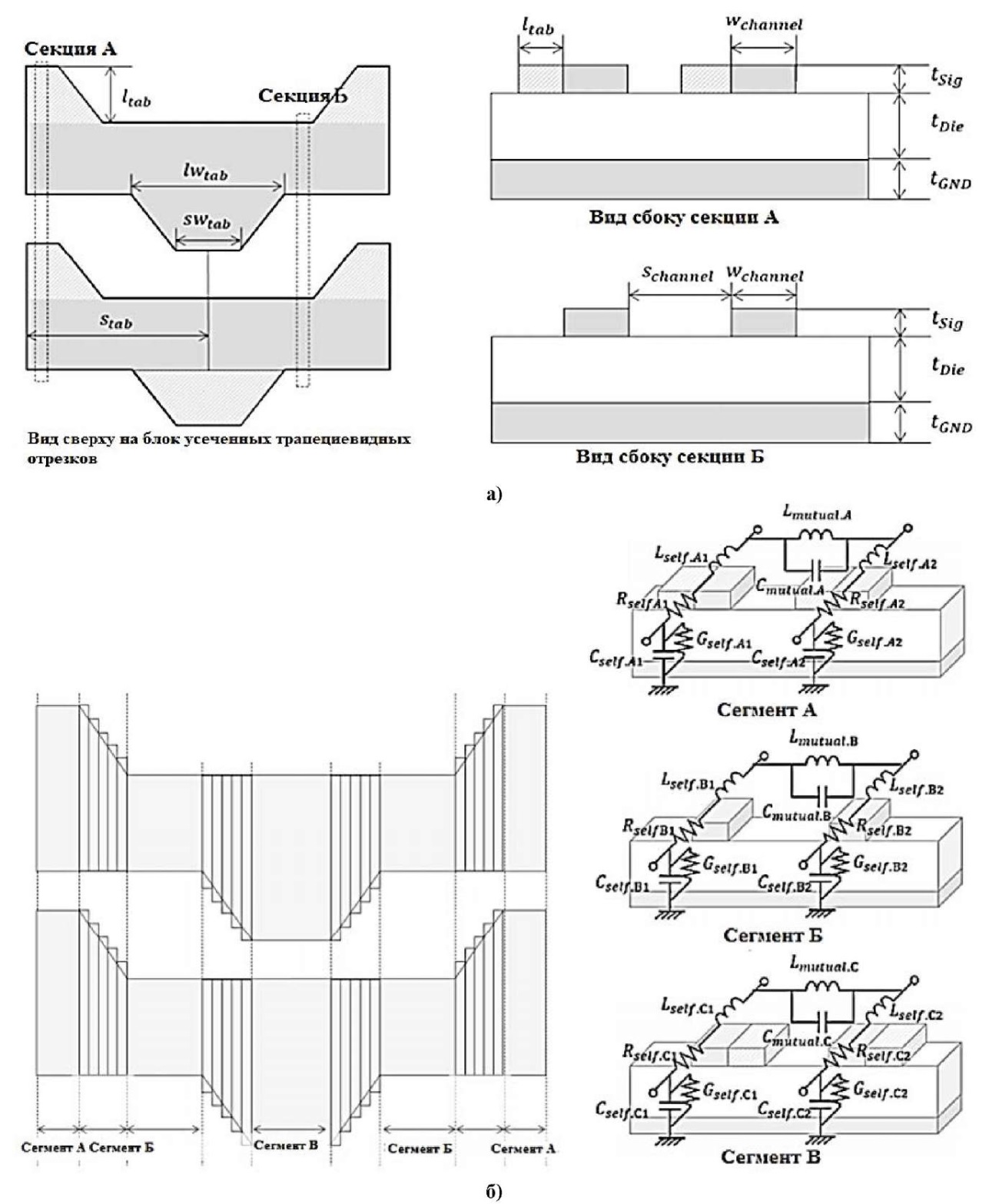
Рис. 5. Виды маршрутизации с одним блоком трапециевидных отрезков: а) виды сверху и сбоку одноблочной трассировки с трапециевидными отрезками и структурными параметрами; б) изображение метода сегментации для моделирования маршрутизации с трапециевидными отрезками с помощью эквивалентной схемы RLC
Примечание: составлено авторами.
Каждый сегмент представляет собой несимметричные связанные микрополосковые линии с изменяющейся шириной канала. Важные параметры сигнальной трассы, такие как потери, FEXT и ВО, зависят от размеров микрополосковой линии.
В связи с этим выполнение анализа трассировки с трапециевидными выступами оказывается более сложным, что обуславливает необходимость моделирования по методу сегментации, как показано на рис. 5б. Расчет емкости и индуктивности производится с учетом изменения ширины и площади связанной микрополосковой линии. Кроме того, для границы между выступами рассчитывается дополнительная емкость края, которая учитывается в эквивалентной модели.
Значения матрицы индуктивности определяются в однородной среде на основе емкости для парной микрополосковой линии, исключая влияние границы выступа.
Таким образом, в данной статье представлен усовершенствованный метод моделирования трассировки с использованием трапециевидных отрезков и метода сегментации, приведенный на рис. 6.
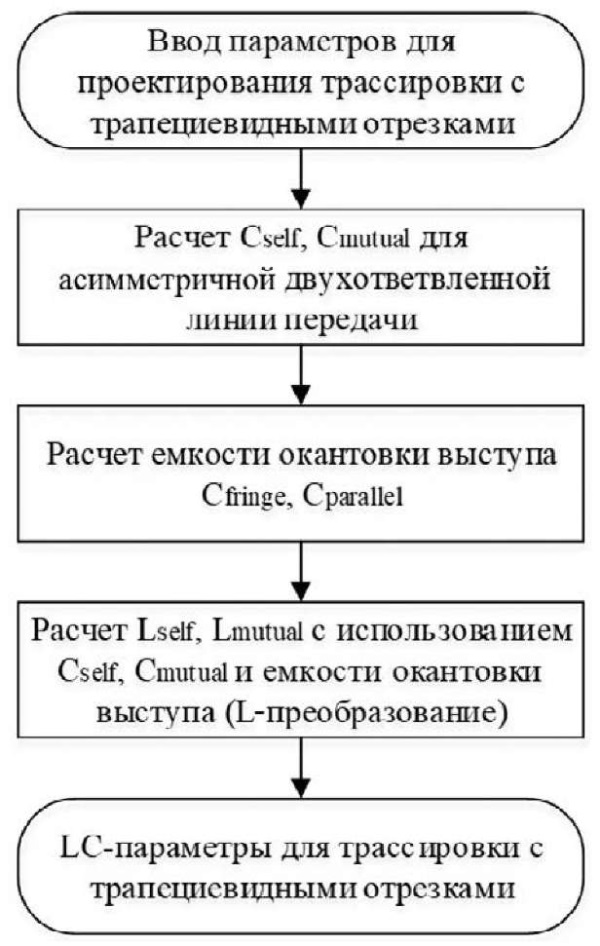
Рис. 6. Блок-схема разработанной методики трассировки с трапециевидными отрезками, основанной на методе сегментации
Примечание: составлено авторами.
Величины собственной и взаимной емкостей несимметрично связанной микрополосковой линии вычисляются на основе эталонного уравнения, полученного из физических параметров проектирования маршрутизации с фиксированными выступами, как указано в табл. 1.
Во-вторых, емкость края Cfringe рассчитывается с применением фиксированных физических параметров разработки трассировки с трапециевидными отрезками. На следующем этапе значения собственной и взаимной емкостей определяются путем вычисления матрицы на основе ранее полученных результатов расчета емкостей и емкости края. Также было введено понятие «L-преобразование» для расчетов матрицы индуктивности, которая включает в себя взаимную емкость и емкость, ограниченную выступами. Используя рассчитанные значения индуктивности и емкости наряду с параметрами сопротивления и проводимости, возможно создать одноблочную модель трассировки с трапециевидными отрезками.
Параметры полной емкости представлены на рис. 7 и зависят от конструктивных характеристик асимметричной микрополосковой линии.
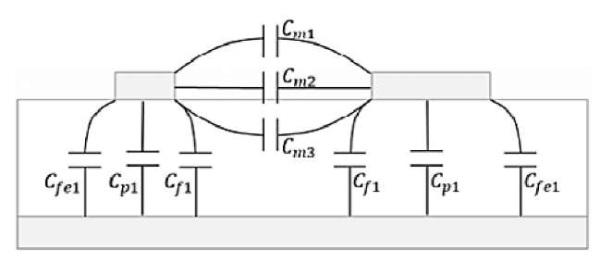
Рис. 7. Вид поперечного сечения соединенных асимметричных микрополосковых линий и параметры емкости
Примечание: составлено авторами.
Матрица емкости C для двухполосной микрополосковой линии имеет вид (4)–(7):
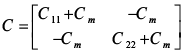 , (4)
, (4)
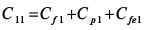 , (5)
, (5)
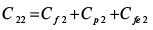 , (6)
, (6)
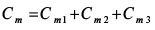 . (7)
. (7)
Матрица C в (4) представляет собой не зависящее от частоты значение, где C11, C22, Cm показывают значения собственной емкости линии 1 и линии 2 на землю и взаимную емкость между линиями 1 и 2 соответственно.
На втором этапе рассчитывается окаймляющая емкость выступа. Результат распределения электрической трассировки с трапециевидными отрезками представлен на рис. 8.
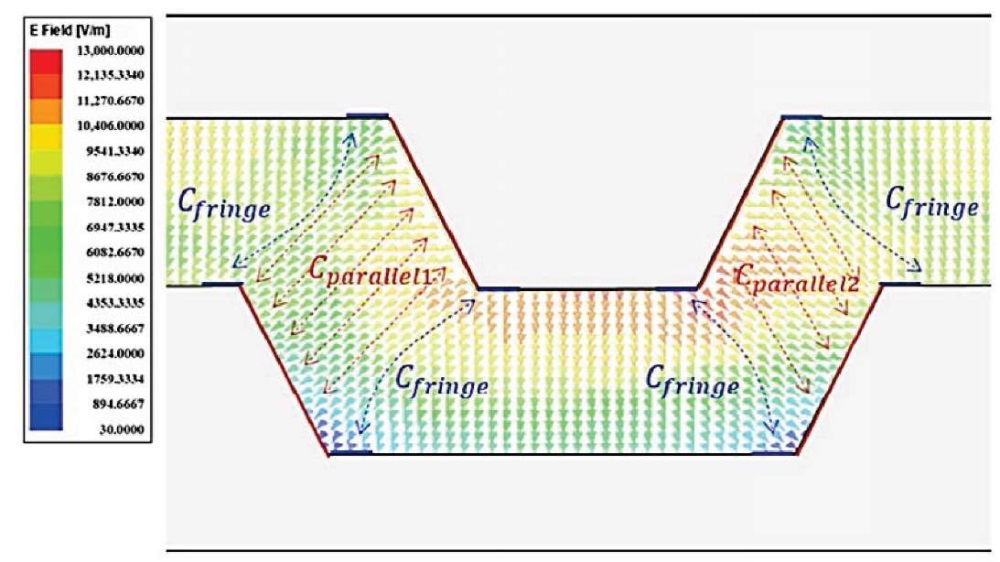
Рис. 8. Моделирование электромагнитного поля для трассировки с трапециевидными отрезками
Примечание: составлено авторами на основании данных, полученных в исследовании.
В общем случае вектор электромагнитного поля микрополосковой линии генерируется в направлении, перпендикулярном направлению электромагнитной волны.
Для косого уклона параллельные поверхности обращены друг к другу, и Cparallet можно рассчитать с использованием (8)–(9):
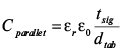 , (8)
, (8)
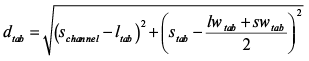 . (9)
. (9)
Для учета наклонного электронного поля, которое создается соседними трапециевидными отрезками, можно ввести дополнительные взаимные емкости Cfringe и Cparallel [5]. Это позволит более точно смоделировать эффект выступов, используя описанные ранее два этапа. Однако для повышения устойчивости моделирования вводится дополнительный шаг. Расчет матрицы индуктивности двухсвязной асимметричной микрополосковой линии L может быть выполнен по (10).
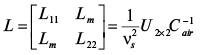 . (10)
. (10)
Эта матрица учитывает как самоиндуктивность каждой полоски, так и взаимную индуктивность между ними. Используя (10), можно рассчитать матрицу емкости C двухсвязной асимметричной микрополосковой линии. Эта матрица включает в себя емкость каждой полоски по отношению к земле и взаимную емкость между полосками.
Объединяя матрицы L и C, полученные на предыдущих этапах, можно сформировать матрицу импеданса Z. Эта матрица импеданса учитывает как индуктивные, так и емкостные эффекты микрополосковой линии. Затем матрица импеданса Z используется в моделировании для определения характеристик распространения сигнала по микрополосковой линии, включая потери и задержки [6–8].
Таким образом, предложенный метод моделирования позволяет более точно учитывать влияние выступов на характеристики микрополосковой линии за счет введения дополнительных этапов и использования матриц индуктивности и емкости. Это приводит к более стабильным и надежным результатам моделирования.
Анализ целостности сигнала при трассировке с трапециевидными отрезками проводился с изменением параметров конструкции при изменении параметра длины выступа ltab, Cfringe и Cparallel. Результаты вносимых потерь, FEXT и импеданса ВО отображаются и сравниваются на рис. 9.
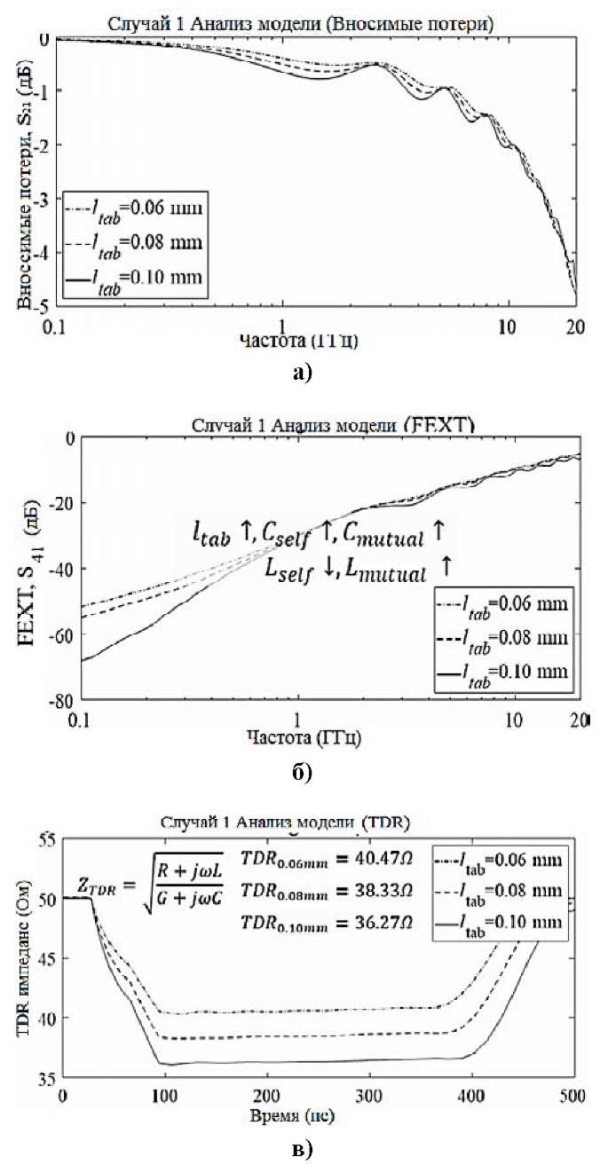
Рис. 9. Анализ вносимых потерь и FEXT в частотной области: а) вносимые потери; б) FEXT; в) результаты импеданса ВО для изменения ltab
Примечание: составлено авторами на основании данных, полученных в исследовании.
При изменении параметра ltab параметры Cfringe и Cparallel изменяются одновременно. Таким образом, с увеличением ltab увеличиваются значения взаимной и собственной емкостей.
ЗАКЛЮЧЕНИЕ
В результате проведенного анализа и моделирования можно сделать вывод о значительном влиянии структуры микрополосковых линий на перекрестные помехи и потерю сигналов в высокочастотных приложениях. Применение трассировки с трапециевидными отрезками направлено на снижение перекрестных помех FEXT. В этом процессе электрическая длина настраивается с помощью рефлектометра и анализа сигналов во временной области. В отличие от традиционных каналов, где ширина и расстояние стабильны, в трассировке с трапециевидными отрезками эти параметры изменяются от сегмента к сегменту, что, в свою очередь, сказывается на значениях емкости и индуктивности.
В представленной работе разработан метод моделирования эквивалентной схемы трассировки на основе сегментационного подхода. Эта модель позволила провести анализ трассировки с трапециевидными отрезками с учетом различных расчетных параметров, основанных на собственной и взаимной емкости и индуктивности.
Учитывая возросший интерес к высокопроизводительным вычислительным системам, возникает необходимость проектирования высокоскоростных каналов передачи сигналов в высокочастотном диапазоне с минимальными потерями, что играет ключевую роль в обеспечении надежной передачи данных.
Список литературы
1. Li L., Wu Z., Yang K. et al. A novel miniature singlelayer eighthmode siw filter with improved outofband rejection // IEEE Microwave and Wireless Components Letters. 2018. Vol. 28, no. 5. P. 407–409. https://10.1109/lmwc.2018.2813883.
2. Packianathan R., Srinivasan R. Comparative study of crosstalk reduction techniques in RF printed circuit board using FDTD method // International Journal of Antennas and Propagation. 2015. 9 p. https://doi.org/10.1155/2015/294590.
3. Турецкий А. В. Хорошайлова М. В., Шамсуддин Н. Х. Обеспечение целостности сигнала в высокоскоростном вычислительном устройстве // Проблемы обеспечения надежности и качества приборов, устройств и систем : сб. науч. тр. Воронеж : Воронежский государственный технический университет, 2023. С. 199–205.
4. Хорошайлова М. В. Архитектура канального кодирования на основе ПЛИС для 5G беспроводной сети с использованием высокоуровневого синтеза // Вестник Воронежского государственного технического университета. 2018. Т. 14, № 2. С. 99–105.
5. Al-Araji Z. H., Swaikat N. A., Muratov A. et al. Modeling and Experimental Research of Vibration n Properties of A Multi-Layer Printed Circuit Board // Proceedings of 4th Scientific International Conference Najaf (SICN), 2019. IEEE, 2019. P. 43–47.
6. Release 2022 R1 Highlights. Ansys Sherlock & Electronics Reliability. URL: https://www.econengineering.com/wp-content/uploads/2022/01/sherlockandelectronics_2022_ansys_econ_engineering.pdf (дата обращения: 05.04.2025).
7. Ling B., Wei K., Wang Z. et al. Experimentally Program Large Magnitude of Poisson’s Ratio in Additively Manufactured Mechanical Metamaterials // International Journal of Mechanical Sciences. 2020. Vol. 173. https://doi.org/10.1016/j.ijmecsci.2020.105466.
8. Wang C., Gu X., Zhu J. et al. Concurrent Design of Hierarchical Structures with Three-Dimensional Parameterized Lattice Microstructures for Additive Manufacturing // Structural and Multidisciplinary Optimization. 2020. Vol. 61. P. 869–894.
Об авторах
А. А. ПироговРоссия
кандидат технических наук, доцент
М. В. Хорошайлова
Россия
кандидат технических наук, доцент
Н. Г. Назаренко
Россия
старший преподаватель
Э. В. Сёмка
Россия
кандидат физико-математических наук, доцент
Рецензия
Для цитирования:
Пирогов А.А., Хорошайлова М.В., Назаренко Н.Г., Сёмка Э.В. Анализ обеспечения целостности сигнала на печатной плате при проектировании высокопроизводительных вычислительных устройств. Вестник кибернетики. 2025;24(2):47-57. https://doi.org/10.35266/1999-7604-2025-2-6
For citation:
Pirogov A.A., Khoroshailova M.V., Nazarenko N.G., Syomka E.V. Signal integrity control analysis on printed circuit board in design of high-performance computing devices. Proceedings in Cybernetics. 2025;24(2):47-57. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-6















