Перейти к:
Метод захвата движущегося объекта манипулятором на основе обучения с подкреплением
https://doi.org/10.35266/1999-7604-2025-2-8
Аннотация
В статье предлагается метод управления манипулятором с использованием обучения с подкреплением в глубоких нейронных сетях для захвата движущихся объектов на конвейерной ленте. В отличие от задач с захватом статичных объектов, данная проблема требует учета динамических факторов, что существенно усложняет процесс управления. Подробно рассматривается физико-кинематическое моделирование манипулятора, а также интеграция параметров манипулятора и движущихся объектов в структуру нейронной сети. Метод протестирован в среде физического моделирования PyBullet.
Ключевые слова
Для цитирования:
Цао И. Метод захвата движущегося объекта манипулятором на основе обучения с подкреплением. Вестник кибернетики. 2025;24(2):66-73. https://doi.org/10.35266/1999-7604-2025-2-8
For citation:
Cao Y. Reinforcement learning-based method for grasping moving object with robotic manipulator. Proceedings in Cybernetics. 2025;24(2):66-73. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-8
ВВЕДЕНИЕ
С развитием искусственного интеллекта за последние годы эксперты и исследователи активно применяют нейронные сети для решения различных задач в робототехнике и автоматизированном производстве [1]. Одной из актуальных и сложных проблем является захват движущихся объектов, так как он требует от манипулятора способности захватывать объекты с высокой вероятностью успеха, а также выполнять захват за время, соответствующее требованиям производственного процесса. Решение этой задачи имеет огромное значение для оптимизации современных производственных процессов и повышения их эффективности.
Pane и соавт. [2] провели эксперименты на манипуляторе UR5 и показали, что использование алгоритмов обучения с подкреплением (Reinforcement learning, RL) позволяет значительно повысить точность управления, при использовании PD-регулятора погрешность позиционирования конечного эффектора составляла около 2 мм, тогда как при применении RL-методов – около 1 мм.
Sekkat и соавт. [3] продемонстрировали, как алгоритмы глубокого обучения на основе DDPG (Deep Deterministic Policy Gradient) могут повысить эффективность манипулятора при использовании решений на основе YOLO для точного позиционирования объектов. В проведенных экспериментах при захвате статических целей была достигнута вероятность успешного захвата на уровне 95,5 %.
N. Marturi и соавт. [4] предложили метод, использующий решатель обратной кинематики (IK) и анализ ошибки в рабочем пространстве (task space error, разница между текущим положением захвата и целевым положением) для выбора оптимальной траектории захвата движущихся объектов в режиме реального времени. Однако этот подход опирается на несколько камер с фиксированным положением.
Захват объекта – это процесс приближения манипулятора к целевому объекту и его фиксации с помощью захватного устройства. В статье предлагается метод, реализованный с использованием открытых библиотек Stable Baselines3 и PyBullet, основная цель исследования – применение метода обучения с подкреплением для решения задачи захвата движущегося объекта на конвейерной ленте.
МАТЕРИАЛЫ И МЕТОДЫ
В данной работе рассматривается управление манипулятором «Franka Emika Panda» [5], обладающим семью степенями свободы. Как показано на рис. 1, каждое из семи сочленений манипулятора c Joint 0…Joint 6 имеет определенный диапазон вращения, обеспечивая высокую гибкость при выполнении задач. Захват манипулятора обладает максимальной шириной раскрытия 8 см, что позволяет работать с объектами различной формы и размеров. Максимальное усилие захвата составляет 70 ньютонов, а предельная скорость движения пальцев захвата – до 0,1 м/с.
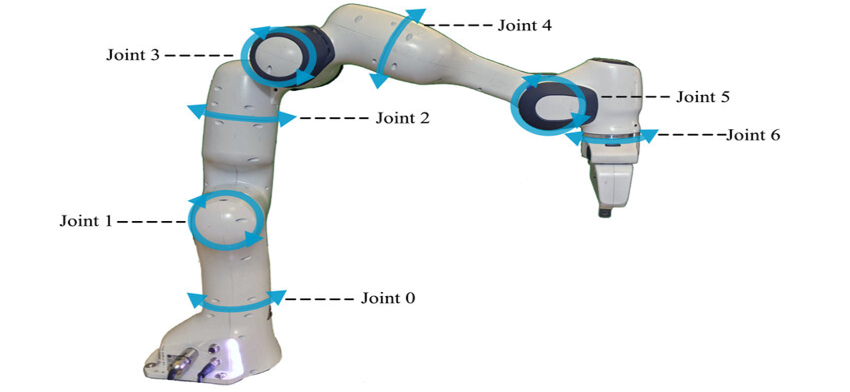
Рис. 1. Манипулятор Franka Emika Panda
Примечание: изображение получено автором по [5].
Постановка задачи. На конвейерной ленте равномерно движется объект цилиндрической формы (диаметр d = 0,04 м, высота h = 0,17 м). Требуется использовать манипулятор для захвата объекта в пределах заданной области P (0,7 м × 0,3 м) за время Т = 14 с, при этом манипулятор не должен соприкасаться с конвейерной лентой, а захват должен контактировать с объектом только в процессе захвата.
Математическая формализация задачи: объект движется равномерно вдоль оси X с постоянной скоростью v0, что описывается уравнением (1):
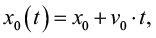 (1)
(1)
где:
x0 – начальное положение объекта, t – текущее время, а v0 – постоянная скорость (например, v0 = 0,05 м/с);
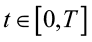 – время (в секундах), в течение которого должен быть выполнен захват;
– время (в секундах), в течение которого должен быть выполнен захват;
T =14 с – ограничение по времени выполнения задачи.
Состояние среды и действия агента зависят от времени (2):
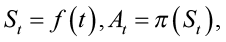 (2)
(2)
где St – 13-мерное наблюдение среды, At – 7-мерное управляющее действие. Подробная структура этих векторов будет описана ниже в разделе, посвященном созданию среды обучения.
Таким образом, задача захвата имеет ярко выраженный динамический характер, поскольку координаты объекта x0 (t), а также состояние среды St и действия агента At явно зависят от времени, такая зависимость делает задачу динамической, требующей обучения моделей, способных учитывать изменения во времени.
Моделирование манипулятора. PyBullet – это открытая библиотека физического моделирования, которая включает в себя встроенные модели различных современных роботов, манипуляторов и других устройств.
В PyBullet производится моделирование среды и объекта, где зеленый цвет – объект, серый цвет – область захвата, голубой цвет – направление движения, красная, зеленая и синяя линии обозначают оси X, Y и Z (рис. 2).
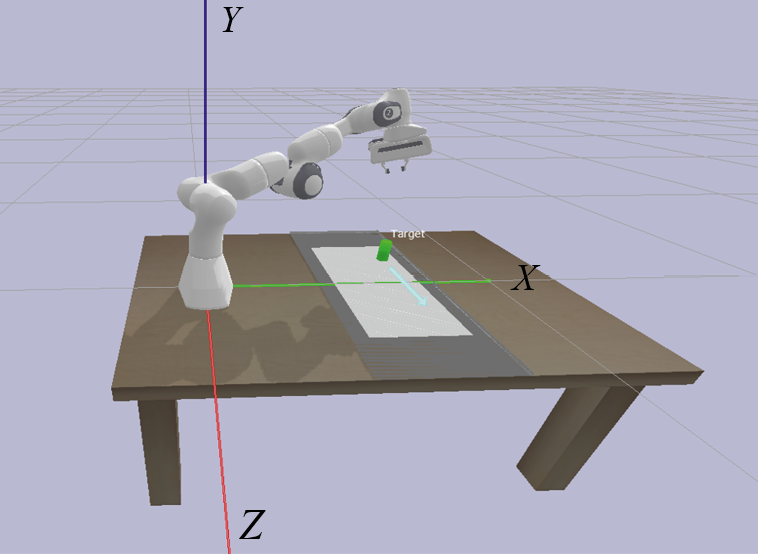
Рис. 2. Симуляционная среда задачи в PyBullet
Примечание: составлено автором.
Преобразование системы координат камеры в мировую систему координат. Передний план и фон на конвейерной ленте используются в качестве маски, и с помощью сегментирующей нейронной сети можно получить пиксельные координаты объекта (u, v) и соответствующее значение глубины dimg из RGBD-камеры. Внутренние параметры камеры представлены матрицей K (3):
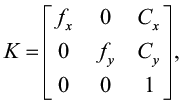 (3)
(3)
где:
fx, fy – фокусное расстояние камеры (в пикселях), вычисляемое по известному углу поля зрения (fov);
cx, cy – положение оптического центра камеры (центр изображения).
Формула для преобразования пиксельных координат (u, v) в координаты камеры pcam = (x_cam, y_cam, z_cam) выглядит следующим образом (4):
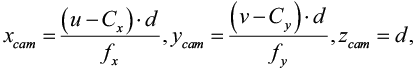 (4)
(4)
где d – истинная глубина, полученная через камеру. Нормализованное значение глубины d_img денормализуется как (5):
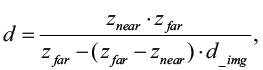 (5)
(5)
где:
z_near (ближняя плоскость): минимальная глубина, которую может видеть камера; в симуляции установлено значение 0.1 метра;
z_far (дальняя плоскость): максимальная глубина, которую может видеть камера; в симуляции установлено значение 10 метров;
d_img – это нормализованное значение глубины, полученное RGBD-камерой после захвата изображения. Диапазон значений d_img – от 0 до 1 и истинная глубина d ≥ 0.
Далее строится матрица внешних параметров E (6):
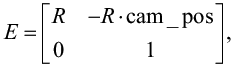 (6)
(6)
где:
cam_pos = координаты камеры, представлены в виде матрицы размером 3×1;
R – матрица поворота, вычисленная для описания вращения координатной системы камеры относительно мировой системы координат. В PyBullet R выражается как (7):
 (7)
(7)
Матрица поворота R формируется из нормализованных векторов направления Forward, Right и Up, представленных как столбцы.
Здесь: focus_pos – координаты фокуса камеры;
вектор Forward = 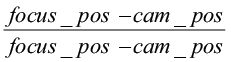 – направление камеры на фокусе;
– направление камеры на фокусе;
вектор Right = 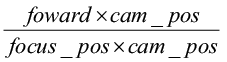 – правое направление камеры;
– правое направление камеры;
вектор Up = Right × Forward – верхнее направление камеры.
Наконец, координаты камеры преобразуются в мировую систему координат. Точка в координатной системе камеры Pworld = (x_w, y_w, zw, 1) может быть преобразована в точку мировой системы координат с помощью матрицы внешних параметров E (8):
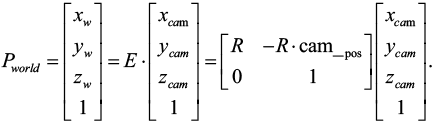 (8)
(8)
За более подробным изложением данного процесса можно обратиться к источнику [6].
Вышеупомянутый процесс обработки от получения изображения до вычисления координат занимает около 50 мс на стандартном настольном компьютере (CPU Intel i7–11800H @ 2,3 ГГц). Таким образом, с помощью приведенных выше вычислений мы можем преобразовать координаты камеры движущегося объекта в координаты мировой системы координат.
Создание среды обучения с подкреплением. Обучение с подкреплением (Reinforcement learning, RL) – метод машинного обучения, при котором агент обучается через взаимодействие с окружающей средой, получая вознаграждение за успешные действия. Обучение с подкреплением на основе окружающей среды с целью максимизации получаемого вознаграждения в процессе обучения, основные компоненты среды обучения с подкреплением включают:
1. Агент (Робот): манипулятор, взаимодействующий со средой, реализована в PyBullet.
2. Среда: симуляционная установка в PyBullet, показанная на рис. 2.
3. Состояние: определяется пространством наблюдений. Входные данные нейронной сети St определяются следующим:
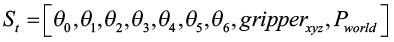
4. Действие: определяется пространством действий. Выходные данные нейронной сети At:
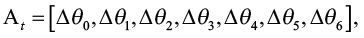
где Δθi – увеличение угла поворота соответствующего сочленения манипулятора относительно предыдущего действия.
Пространство наблюдений – это множество всех возможных состояний среды, в нашем случае оно реализуется в виде 13-мерного вектора признаков, включающего параметры манипулятора и объекта. Аналогично пространство действий – это множество всех допустимых действий, представленных 7-мерным вектором, соответствующим приращениям углов сочленений манипулятора.
5. Вознаграждение: функция R обратной связи для оценки действия A.
Захват считается успешным, если манипулятор фиксирует объект с точностью не более 2 см, при этом на всем протяжении движения отсутствуют столкновения сочленений с объектом. Учитывая максимальную скорость закрытия захвата (0,1 м/с), такие условия обеспечивают оптимальный момент захвата.
Обучение с подкреплением включает следующие этапы:
Шаг 1. Инициализация параметров: манипулятор устанавливается в начальное положение, а объект появляется в случайной позиции в пределах рабочей области.
Шаг 2. Наблюдение и действие: на основе текущего состояния сети подается на вход наблюдение St, сеть принимает решение об изменении углов сочленений At.
Шаг 3. Обновление состояния: новое состояние получается в результате выполнения действия манипулятором и движения объекта по конвейеру.
Шаг 4. Вознаграждение: сеть получает вознаграждение Rt за успешное выполнение задачи захвата или штраф за отклонение от объекта (9),
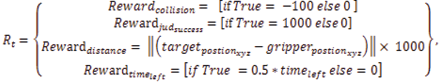 (9)
(9)
где:
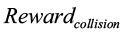 – штраф за столкновения, направленный на то, чтобы манипулятор избегал ударов;
– штраф за столкновения, направленный на то, чтобы манипулятор избегал ударов;
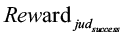 – дополнительное вознаграждение за выполнение задания;
– дополнительное вознаграждение за выполнение задания;
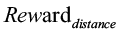 – вознаграждение, поощряющее сближение захвата с целью;
– вознаграждение, поощряющее сближение захвата с целью;
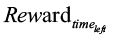 – вознаграждение, основанное на оставшемся времени после выполнения задачи, стимулирующее более быстрое выполнение.
– вознаграждение, основанное на оставшемся времени после выполнения задачи, стимулирующее более быстрое выполнение.
Шаг 5. Корректировка параметров: обновление параметров нейронной сети.
Шаг 6. Повторить Шаг 1–5.
Процесс показан на рис. 3.
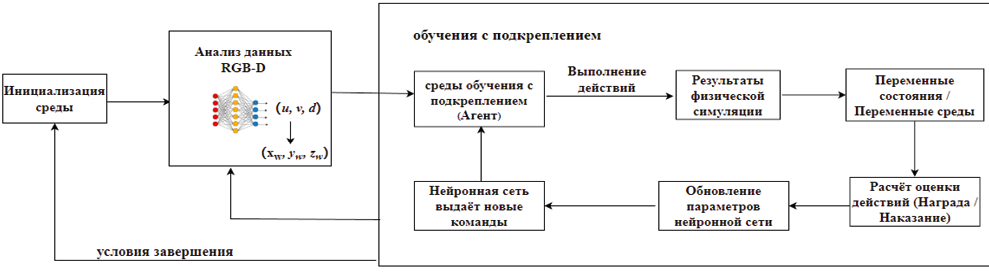
Рис. 3. Схема работы системы управления манипулятора
Примечание: составлено автором.
В этой реализации были протестированы различные алгоритмы обучения с подкреплением, представленные в библиотеке Stable Baselines3, включая DDPG [10], TD3 (Twin Delayed Deep Deterministic Policy Gradient) [11], SAC (Soft Actor-Critic) [12] и PPO (Proximal Policy Optimization) [13].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В процессе экспериментов были протестированы 800 эпизодов на стандартном настольном компьютере с процессором Intel Core i7–11800H. Каждый эпизод содержал 30 000 временных шагов, общий шаг обучения составляет 24 миллиона раз. Для оценки предложенного метода управления манипулятором на основе нейронных сетей мы провели тестирование с использованием четырех современных и популярных алгоритмов обучения с подкреплением: DDPG, TD3, SAC и PPO. Результаты процесса обучения задачи были записаны в TensorBoard (рис. 4):
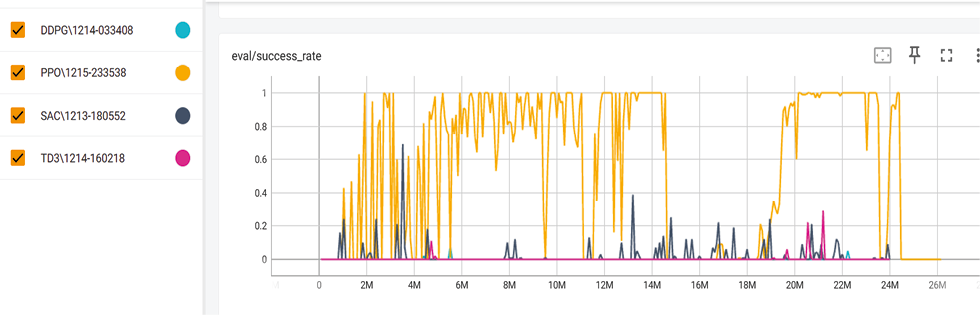
Рис. 4. Процент успеха за итерации
Примечание: составлено автором.
На рис. 4 представлено изменение уровня успешности в зависимости от числа шагов обучения (ось абсцисс, млн). По оси ординат отложен средний уровень успешности, полученный в результате оценки текущей стратегии в течение 10 эпизодов. Эти данные записываются как eval/success_rate и отображаются в TensorBoard. Можно сделать следующие выводы: алгоритм PPO демонстрирует высокий уровень успешности выполнения задачи. По мере увеличения количества шагов обучения увеличивается и диапазон, в котором достигается 100 % успешности. Алгоритмы SAC и TD3 показывают средние результаты – в пределах 40–60 %, а DDPG демонстрирует наименьший уровень успешности – менее 10 %.
Рис. 5 иллюстрирует производительность различных алгоритмов в условиях случайного тестирования. Можно увидеть, что при случайном тестировании PPO завершает захват еще до прохождения половины серой области, тогда как SAC и TD3, по сравнению с PPO, требуют преодоления дополнительного расстояния, а DDPG выходит за пределы серой области.
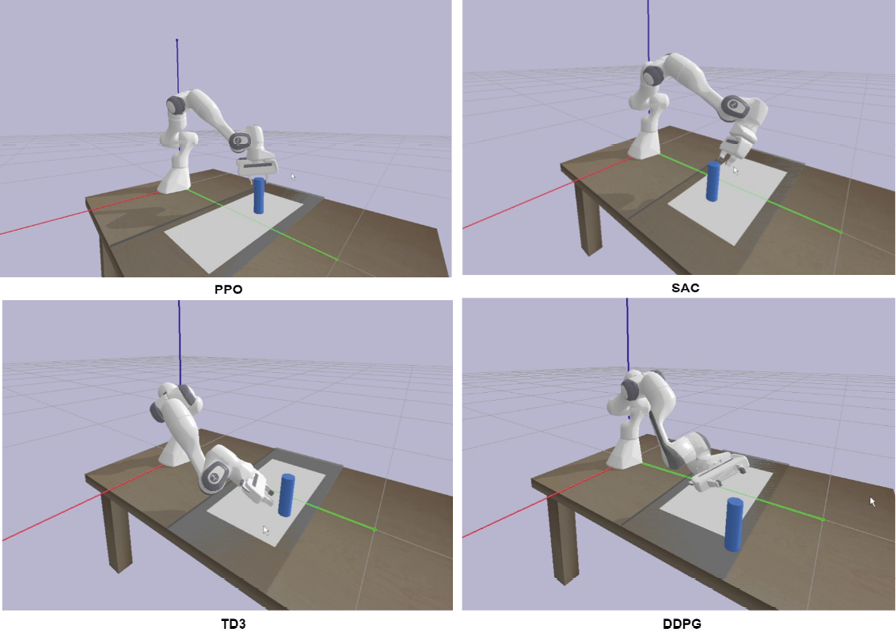
Рис. 5. Результаты различных алгоритмов при случайном тестировании
Примечание: составлено автором.
Обобщение результатов различных алгоритмов приведено в таблице. Чем выше среднее вознаграждение, тем быстрее выполняется задача захвата и тем лучше общая производительность.
Таблица
Сравнение производительности различных алгоритмов
Предобученные алгоритмы | Скорость рассуждения сети (мс) | Количество временных шагов | Процент успеха на 1000 раз тестов ( %) | Среднее награждение Rt | Время обучения (чч.мм) |
DDPG | < 2 | 213,8 | 3,1 | 660,5 | 9 ч 15 м |
TD3 | < 2 | 164,1 | 36,3 | 1188,6 | 8 ч 51 м |
SAC | < 2 | 269,1 | 68,1 | 1397,2 | 9 ч 21 м |
PPO | < 2 | 120,5 | 100 | 2239,9 | 3 ч 39 м |
Примечание: составлено авторами.
ЗАКЛЮЧЕНИЕ
В данной статье представлено применение нейронных сетей для обучения с подкреплением для решения задачи захвата манипулятором объектов, равномерно движущихся по поверхности, аналогичной конвейерной ленте. Проверка метода проводилась на виртуальной платформе физического моделирования, что подтвердило его применимость и эффективность. В качестве предобученных нейронных сетей были использованы популярные модели PPO, DDPG, SAC и TD3, а также детально описаны этапы решения данной задачи с использованием открытых нейросетевых моделей. Полученные результаты могут служить основой для дальнейших исследований.
В целом обучение с подкреплением позволяет успешно захватывать объекты, движущиеся с низкой скоростью – около 3–5 м в минуту. Дальнейшие направления исследований могут включать изучение использования мобильных роботов для захвата объектов, движущихся с более высокой скоростью.
Список литературы
1. Shuzhi S. G., Hang C. C., Woon L. C. Adaptive neural network control of robot manipulators in task space // IEEE transactions on industrial electronics. 1997. No. 6. P. 746–752.
2. Pane Y. P., Nageshrao S. P., Kober J. et al. Reinforcement learning based compensation methods for robot manipulators // Engineering Applications of Artificial Intelligence. 2019. Vol. 78. P. 236–247.
3. Sekkat H., Tigani S., Saadane R. et al. Vision-based robotic arm control algorithm using deep reinforcement learning for autonomous objects grasping // Applied Sciences. 2021. No. 11. P. 7917.
4. Marturi N., Kopicki M., Rastegarpanah A. et al. Dynamic grasp and trajectory planning for moving objects // Autonomous Robots. 2019. No. 43. P. 1241–1256.
5. Reed A., Albin D., Pasricha A. et al. Transformer-based Learning Models of Dynamical Systems for Robotic State Prediction. 2024. https://doi.org/10.21203/rs.3.rs-3919154/v1.
6. Цао И. Метод визуально управляемого захвата 7-степенного манипулятора на основе обучения с подкреплением // Вестник кибернетики. 2025. Т. 24, № 1. С. 31–38.
7. Lillicrap T. P., Hunt J. J., Pritzel A. et al. Continuous control with deep reinforcement learning // arXiv preprint arXiv:1509.02971. 2015.
8. Fujimoto S., Hoof H., Meger D. Addressing function approximation error in actor-critic methods // Proceedings of the 35th International conference on machine learning, 2018, Stockholm. PMLR, 2018. P. 1587–1596.
9. Haarnoja T., Zhou A., Abbeel P. et al. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor // Proceedings of the 35th International conference on machine learning, 2018, Stockholm. PMLR, 2018. P. 1861–1870.
10. Schulman J., Wolski F., Dhariwal P. et al. Proximal policy optimization algorithms // arXiv preprint arXiv: 1707.06347. 2017.
Об авторе
И. ЦаоРоссия
аспирант
Рецензия
Для цитирования:
Цао И. Метод захвата движущегося объекта манипулятором на основе обучения с подкреплением. Вестник кибернетики. 2025;24(2):66-73. https://doi.org/10.35266/1999-7604-2025-2-8
For citation:
Cao Y. Reinforcement learning-based method for grasping moving object with robotic manipulator. Proceedings in Cybernetics. 2025;24(2):66-73. (In Russ.) https://doi.org/10.35266/1999-7604-2025-2-8















