Перейти к:
ОЦЕНКА ЭФФЕКТИВНОСТИ ТЕСТОВ ГЕТЕРОСКЕДАСТИЧНОСТИ
https://doi.org/10.35266/1999-7604-2024-1-11
Аннотация
В данной статье рассматривается эффективность различных статистических тестов, предназначенных для обнаружения гетероскедастичности в модели. Описывается методология исследования, принцип построения синтетических данных с разными типами гетероскедастичности. Приведены детальные результаты анализа, определены лучшие тесты для решения задач детектирования гомо- и гетероскедастичности. Применен аппарат деревьев классификации для определения лучших тестов в зависимости от свойств выборки, показано наличие данных закономерностей. Отмечено, что в практических работах необходимо проведение дополнительных исследований, направленных на установление лучшего статистического теста при наблюдаемых свойствах данных. Кроме того, сделан вывод о том, что для рассматриваемых типов гетероскедастичности все выбранные тесты показывают значительный процент ошибок, что говорит о необходимости продолжения соответствующих теоретических исследований и разработке новых способов детектирования разных форм гетероскедастичности.
Ключевые слова
Для цитирования:
Черемухин А.Д. ОЦЕНКА ЭФФЕКТИВНОСТИ ТЕСТОВ ГЕТЕРОСКЕДАСТИЧНОСТИ. Вестник кибернетики. 2024;23(1):81-88. https://doi.org/10.35266/1999-7604-2024-1-11
For citation:
Cheremukhin A.D. EVALUATING EFFECTIVENESS OF TESTS FOR HETEROSCEDASTICITY. Proceedings in Cybernetics. 2024;23(1):81-88. (In Russ.) https://doi.org/10.35266/1999-7604-2024-1-11
ВВЕДЕНИЕ
Активное использование методов анализа данных для решения большого комплекса практических задач актуализировало и вопрос о границах применимости тех или иных методов. Например, для случая классической регрессии общеизвестно, что метод наименьших квадратов дает несмещенные и эффективные оценки коэффициентов только при выполнении условий Гаусса – Маркова. В противном случае возможно получение смещенных оценок коэффициентов, что может привести к серьезным ошибкам при внедрении модели на практике.
Среди всех условий Гаусса – Маркова самым сложно проверяемым является условие на гомоскедастичность – условие на отсутствие зависимости между дисперсией ошибки модели и значениями независимой переменной. Однако в последнее время в разных программных пакетах (например, в пакете skedastic для языка R) появилось значительное количество реализаций разных статистических тестов, проверяющих гипотезу о гомоскедастичности остатков.
Большое количество теоретических подходов к исследованию понятия гомоскедастичности привело к появлению значительного числа тестов, проверяющих разные типы зависимостей между ошибками модели и величиной независимой переменной, – а это значит, что некоторые тесты гомоскедастичности эффективны при одних входных данных, а другие – при других.
Наличием большого числа тестов можно объяснить и частое игнорирование исследователями в разных сферах науки [1][2] процедуры оценки выполнимости Гаусса – Маркова.
Целью данной работы является обнаружение с помощью вычислительного эксперимента самых эффективных статистических тестов для разных случаев гетероскедастичности.
К вопросу оценки эффективности тестов гетероскедастичности исследователи периодически возвращаются – можно выделить работы [3–7]. В отличие от последней работы [7] в этой сфере, данное исследование сосредоточено на моделях гетероскедастичности, в которых значение ошибок зависит от значений независимой переменной; кроме того, исследуется не только эффективность тестов в плане определения гетероскедастичности, но и их эффективность в плане определения гомоскедастичности.
МАТЕРИАЛЫ И МЕТОДЫ
Все расчеты, проведенные в ходе данного исследования, были выполнены с помощью языка R. В качестве объектов изучения были взяты статистические тесты, реализованные в пакете skedastic: Анкомба [8], BAMSET-тест (модификация М-теста Бартлетта, выполненная Рамсеем [9]), Бикеля [10], Бройша – Погана [11], Кука – Вейзеберга [12], Эванса – Кинга [13], Голдфильда – Квандта [14], Харрисона – Маккэйба [15], Хорна [16], Симонова – Цая [17], Вербыла [18], Уайта [19], Уилкокса – Келемана [20], Юсе [21], Чжоу [22].
Общая концепция оценки эффективности тестов основана на создании синтетических данных, по части которых мы точно знаем, что гетероскедастичности там нет, а по части – точно знаем, что она есть. Указанные выше тесты, однако, различаются по характеру рассматриваемой зависимости между ошибками и значениями независимой переменной. Поэтому для обобщенной оценки эффективности тестов использовались данные, сгенерированные по различным моделям:
– модель линейной зависимости с остатками, подчиненными нормальному закону распределения;
– модель линейной зависимости с нормально распределенными остатками, значение которых гиперболически зависит от значений независимой переменной:
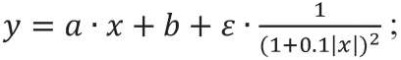 (1)
(1)
– модель линейной зависимости с нормально распределенными остатками, значение которых уменьшается при уменьшении значений независимой переменной:
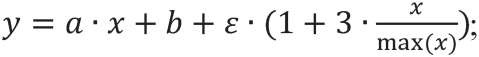 (2)
(2)
– модель линейной зависимости с нормально распределенными остатками, значение которых уменьшается при возрастании значений независимой переменной:
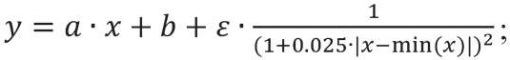 (3)
(3)
– модель линейной зависимости с нормально распределенными остатками, значение которых увеличивается при возрастании значений независимой переменной:
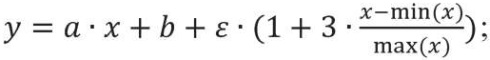 (4)
(4)
– модель линейной зависимости с нормально распределенными остатками, знак которых различен для разных частей выборки:
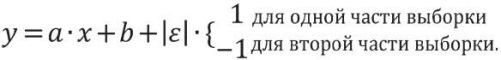 (5)
(5)
Графическое изображение всех шести типов синтетических данных, на которых оценивается эффективность тестов, представлено на рисунке.
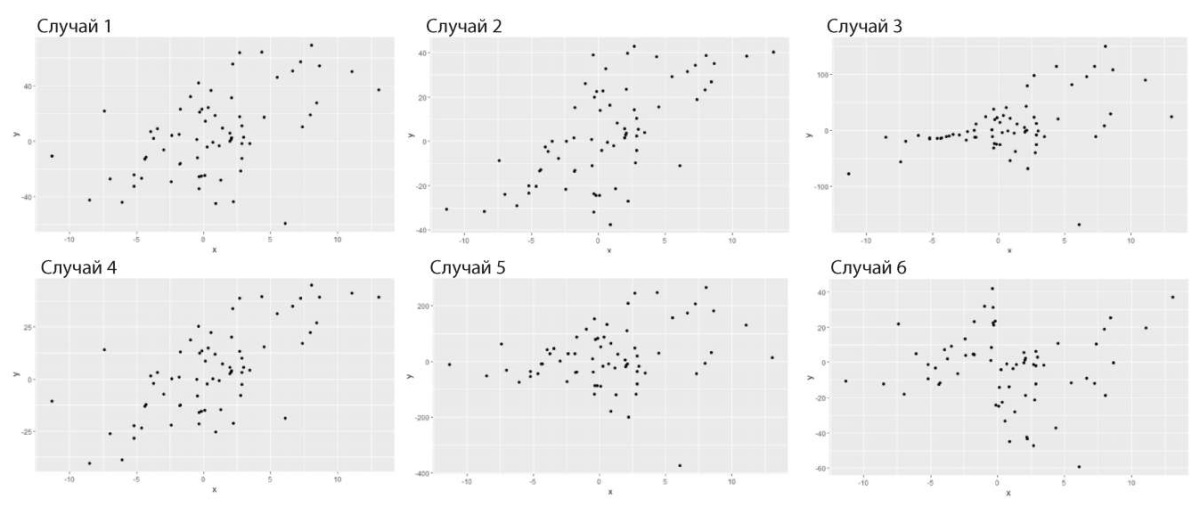
Рисунок. Графическое отображение используемых шести типов синтетических данных
Примечание: составлено автором на основании данных, полученных в исследовании.
Общий алгоритм генерации одного экземпляра синтетических данных для исследования состоит из следующих шагов:
– определяется размер выборки (случайно выбирается число из интервала [ 1,5;3], которое потенцируется по основанию 10 и округляется – количество элементов в выборке, таким образом, может быть от 30 до 1 000);
– генерируются значения независимой переменной (из нормального распределения, среднее значение которого находится в диапазоне от 0,1 до 1 000, а стандартное отклонение меняется от 1 до 5);
– генерируется параметр a линейной зависимости (случайно выбирается число из интервала [ 1,5;3], которое потенцируется по основанию 2 и округляется до сотых);
– генерируется параметр b линейной зависимости (выбирается случайно из интервала, образованного максимальным и минимальным значением независимой переменной);
– рассчитывается величина зависимой переменной без учета остатков, и на основе ее дисперсии генерируется вектор ошибок (ошибки распределены нормально, их среднее равно 0, среднеквадратическое отклонение выбирается из диапазона от среднеквадратического отклонения зависимой переменной до удвоенного значения среднеквадратического отклонения);
– рассчитывается доля значений для модели 6, которая определяет процент ошибок, взятых с положительным знаком;
– рассчитываются шесть векторов значений зависимой переменной для разных моделей гетероскедастичности.
Данный цикл был повторен 10 000 раз – в результате было получено 1 000 датафреймов разного размера, с разными параметрами независимой переменной, распределения ошибок и линейной зависимости.
После этого всеми вышеперечисленными статистическими тестами на уровне значимости в 0,05 были исследованы сгенерированные датафреймы. Полученные результаты исследовались двумя способами:
– путем построения сравнительных таблиц по тестам;
– через использование деревьев решений для выявления оптимального теста в зависимости от параметров выборок.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Сравнительная оценка эффективности тестов представлена ниже (таблица).
Таблица
Процент ошибок статистических тестов для разных моделей гетероскедастичности
Тест | Номер модели | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
Анкомба | 4,62 | 83,71 | 37,12 | 16,20 | 32,50 | 100,00 |
BAMSET | 0,19 | 43,93 | 32,43 | 20,93 | 16,19 | 39,47 |
Бикеля | 4,67 | 99,93 | 95,30 | 95,37 | 95,33 | 67,47 |
Бройша – Погана | 4,62 | 83,71 | 32,53 | 16,16 | 32,46 | 100,00 |
Кука – Вейзеберга | 0,02 | 83,63 | 27,91 | 20,76 | 20,91 | 99,99 |
Эванса – Кинга | 39,41 | 62,77 | 16,32 | 11,56 | 16,28 | 76,85 |
Голдфильда – Квандта | 0,04 | 78,89 | 32,49 | 16,33 | 20,87 | 83,84 |
Харрисона – Маккэйба | 11,58 | 67,40 | 32,56 | 20,91 | 32,52 | 99,89 |
Хорна | 4,7 | 79,01 | 32,49 | 16,32 | 32,46 | 99,99 |
Симонова – Цая | 0,02 | 83,63 | 27,91 | 20,76 | 20,91 | 99,99 |
Вербыла | 0,02 | 83,63 | 27,91 | 20,76 | 20,90 | 99,99 |
Уайта | 0,14 | 71,83 | 32,50 | 20,76 | 48,65 | 99,99 |
Уилкокса – Келемана | 0 | 95,25 | 48,70 | 16,39 | 37,09 | 99,96 |
Юсе | 0 | 60,35 | 53,36 | 72,07 | 99,99 | 99,88 |
Чжоу | 11,68 | 99,98 | 27,91 | 83,60 | 55,95 | - |
Примечание: составлено по результатам расчетов автора.
Согласно данным таблицы, можно сделать следующие выводы:
– тесты Юсе и Уилкокса – Келемана на представленных данных показали 100-процентную точность на данных без гетероскедастичности. Соответствующие тесты показывают крайне низкую вероятность ошибок первого рода, т. е. ошибочного отклонения гипотезы о гомоскедастичности;
– для случая гетероскедастичности при гиперболической зависимости остатков от значений независимой переменной (модель 2) все тесты, кроме BAMSET-теста, показывают более 50 % ошибок. Большая вероятность ошибок второго рода говорит об отсутствии надежных способов идентификации данного типа гетероскедастичности;
– для случая гетероскедастичности с уменьшением значений ошибок при уменьшении значений независимой переменной (модели 3 и 4) констатируем, что наилучший результат показывает тест Эванса – Кинга – примерно в 85–88 % случаев он позволил верно отвергнуть нулевую гипотезу о гомоскедастичности;
– для случая гетероскедастичности с увеличением значения ошибок при возрастании значений независимой переменной (модель 5) лучшие результаты показывают BAMSET-тест и тест Эванса – Кинга – в среднем в 1 случае из 12 они не позволяют отвергнуть ошибочную гипотезу о гомоскедастичности;
– для случая гетероскедастичности с изменением знака (модель 6) все тесты, кроме BAMSET-теста, показывают более 50 % ошибок. Большая вероятность ошибок второго рода говорит об отсутствии надежных способов идентификации данного типа гетероскедастичности.
Общий вывод позволяет констатировать большую эффективность BAMSET-теста и теста Эванса – Кинга в части сравнительно низкой вероятности ошибки второго рода и тестов Юсе, Уилкокса – Келемана в части низкой вероятности ошибки первого рода.
Однако сделанные выводы являются общими – возможно, при некоторых особенностях выборки некоторые статистические тесты обладают существенно большей эффективностью, чем другие. Для диагностики этого нами был использован метод деревьев классификации. Его применение к смоделированным данным позволило сделать следующие выводы:
– для случая с отсутствием гетероскедастичности все 15 рассмотренных тестов верно принимают нулевую гипотезу при следующих условиях: коэффициент корреляции между зависимой и независимой переменной меньше 0,747, стандартное отклонение независимой переменной больше 17,48;
– для случая гетероскедастичности при гиперболической зависимости остатков от значений независимой переменной (модель 2) 9 из 15 тестов верно отвергают нулевую гипотезу при следующих условиях: истинный коэффициент наклона в линейной модели находится в диапазоне от 0,36 до 6,42, а соотношение коэффициента наклона к стандартному отклонению независимой переменной меньше 0,636;
– для случая гетероскедастичности с уменьшением значений ошибок при уменьшении значений независимой переменной (модель 3) 13 из 15 тестов верно отвергают нулевую гипотезу при небольших значениях независимой переменной (среднее значение независимой переменной меньше 4,73);
– для случая гетероскедастичности с уменьшением значений ошибок при уменьшении значений независимой переменной (модель 4) 14 из 15 тестов верно отвергают нулевую гипотезу при выполнении следующих условий: стандартное отклонение зависимой переменной меньше 22,1, истинный коэффициент наклона в линейной модели меньше 0,847, коэффициент корреляции между зависимой и независимой переменной больше 0,95;
– для случая гетероскедастичности с увеличением значения ошибок при возрастании значений независимой переменной (модель 5) 12 из 15 тестов верно отвергают нулевую гипотезу при коэффициенте корреляции между зависимой и независимой переменной вне диапазона (0,38;0,52);
– для случая гетероскедастичности с изменением знака ошибок (модель 6) 5 тестов из 15 верно отвергают нулевую гипотезу при среднем значении зависимой переменной от 637 до 715.
Далее был проведен более детальный анализ по областям эффективности тестов. Для случая с отсутствием гетероскедастичности можно сделать следующие выводы:
– если среднее значение независимой переменной меньше 87,37, то в 99,7 % случаев лучшим является тест Бикеля;
– если среднее значение независимой переменной больше 87,37, соотношение коэффициента наклона к стандартному отклонению независимой переменной меньше 0,74, среднее значение независимой переменной меньше 906, то в 99,5 % случаев лучшим является тест Голдфельда – Квандта;
– если среднее значение независимой переменной больше 87,37, соотношение коэффициента наклона к стандартному отклонению независимой переменной меньше 0,74, среднее значение независимой переменной больше 906, то в 98,2 % случаев лучшим является тест Бикеля;
– если среднее значение независимой переменной больше 87,37, соотношение коэффициента наклона к стандартному отклонению независимой переменной больше 0,74, то в 99,9 % случаев лучшим является тест Уайта.
Для случаев гетероскедастичности при гиперболической зависимости остатков от значений независимой переменной (модель 2) можно сделать следующие выводы:
– если среднеквадратичное отклонение зависимой переменной меньше 39,6, то в 99,3 % случаев лучшим является тест Эванса – Кинга;
– если среднеквадратичное отклонение зависимой переменной больше 39,6, среднее значение зависимой переменной меньше 33,42, то в 99,9 % случаев лучшим является BAMSET-тест.
Для случаев гетероскедастичности с уменьшением значений ошибок при уменьшении значений независимой переменной (модель 3) можно сделать следующие выводы:
– если среднее значение независимой переменной меньше 87,37, соотношение коэффициента наклона к стандартному отклонению независимой переменной меньше 6,24, то в 99,9 % случаев лучшим является тест Чжоу;
– если среднее значение независимой переменной больше 87,37, а среднее значение зависимой переменной больше 764,2, то в 99,4 % случаев лучшим является тест Эванса – Кинга;
– если среднее значение независимой переменной больше 87,37, среднее значение зависимой переменной меньше 764,2, стандартное отклонение зависимой переменной меньше 188,7, то лучшим является тест Бикеля;
– если среднее значение независимой переменной больше 87,37, среднее значение зависимой переменной меньше 764,2, стандартное отклонение зависимой переменной больше 188,7, то лучшим является тест Харрисона – Маккейба.
Для случаев гетероскедастичности с уменьшением значений ошибок при уменьшении значений независимой переменной (модель 4) можно сделать следующие выводы:
– если коэффициент корреляции между зависимой и независимой переменной больше 0,956, то лучшим является тест Чжоу;
– если коэффициент корреляции между зависимой и независимой переменной меньше 0,956, стандартное отклонение зависимой переменной меньше 16,46, то в 99,9 % случаев лучшим является BAMSET-тест;
– если коэффициент корреляции между зависимой и независимой переменной меньше 0,956, стандартное отклонение зависимой переменной больше 16,46, то в 99,7 % случаев лучшим является тест Эванса – Кинга.
Для случаев гетероскедастичности с увеличением значения ошибок при возрастании значений независимой переменной (модель 5) можно сделать следующие выводы:
– если коэффициент наклона в модели меньше 5,13, а коэффициент корреляции между зависимой и независимой переменной меньше 0,73, то в 99,6 % лучшим является тест Харрисона – Маккейба;
– если коэффициент наклона в модели меньше 5,13, а коэффициент корреляции между зависимой и независимой переменной больше 0,73, то в 99,6 % лучшим является тест Эванса – Кинга;
– если коэффициент наклона в модели больше 5,13, соотношение коэффициента наклона к стандартному отклонению независимой переменной меньше 0,36, то лучшим является тест Голдфильда – Квандта;
– если коэффициент наклона в модели больше 5,13, соотношение коэффициента наклона к стандартному отклонению независимой переменной больше 0,36, стандартное отклонение зависимой переменной меньше 37,2, то в 99,8 % случаев лучшим является тест Бикеля;
– если коэффициент наклона в модели больше 5,13, соотношение коэффициента наклона к стандартному отклонению независимой переменной больше 0,36, стандартное отклонение зависимой переменной больше 37,2, то в 99,5 % случаев лучшим является тест Чжоу.
Для случаев гетероскедастичности с изменением знака ошибок (модель 6) можно сделать следующие выводы:
– если среднее значение независимой переменной больше 87,4, то в 99,9 % случаев лучшим является тест Бикеля;
– если среднее значение независимой переменной меньше 87,4, коэффициент наклона в модели меньше трех, то лучшим является тест Юсе;
– если среднее значение независимой переменной меньше 87,4, коэффициент наклона в модели больше трех, стандартное отклонение независимой переменной меньше 24,2, то в 99,6 % случаев лучшим является BAMSET-тест;
– если среднее значение независимой переменной меньше 87,4, коэффициент наклона в модели больше трех, стандартное отклонение независимой переменной больше 24,2, то в 99,6 % случаев лучшим является тест Эванса – Кинга.
ЗАКЛЮЧЕНИЕ
Анализ полученных результатов позволил сделать несколько теоретических и прикладных выводов.
Во-первых, в прикладных задачах, в зависимости от особенностей их постановки, в общем случае лучше использовать тесты Юсе и Уилкокса – Келемана или тест Эванса – Кинга вместе с BAMSET-тестом.
Во-вторых, показано наличие существенной зависимости эффективности рассмотренных статистических тестов от параметров выборки, к которой они применяются. Соответственно, в практических исследованиях рекомендуется сначала проведение вспомогательных работ, направленных на установление эффективности тестов гетероскедастичности при имеющихся данных с конкретными свойствами.
В-третьих, при некоторых типах гетероскедастичности все рассмотренные тесты показывают значительный процент ошибок. Это говорит о необходимости продолжения соответствующих теоретических исследований и разработке новых способов детектирования разных форм гетероскедастичности.
Список литературы
1. Асансеитова С. М., Ковалева Э. В., Свинухов В. Г. Оценка влияния экпорта и прямых иностранных инвестиций на ВВП на примере стран-членов ЕАЭС // Вестник НГИЭИ. 2018. № 9. С. 60‒70.
2. Молодченков Д. А. Результаты экспериментальных исследований профилеобразующего катка для гребневого посева пропашных культур // Вестник НГИЭИ. 2018. № 9. С. 114‒127.
3. Lyon J. D., Tsai C.-L. A comparison of tests for heteroscedasticity. The Statistician. 1996;45(3):337–349.
4. Harvey A. C., Phillips G. D. A. A comparison of the power of some tests for heteroskedasticity in the general linear model. Journal of Econometrics. 1974;2:307–316.
5. Griffi ths W. E., Surekha K. A Monte Carlo evaluation of the power of some tests for heteroscedasticity. Journal of Econometrics. 1986;31(2):219–231.
6. Dufour J.-M., Khalaf L., Bernard J.-T. et al. Simulation-based fi nite-sample tests for heteroskedasticity and ARCH effects. Journal of Econometrics. 2004;122(2):317–347.
7. Uyanto S. S. Monte Carlo power comparison of seven most commonly used heteroscedasticity tests. Communications in Statistics – Simulation and Computation. 2019;51(4):2065–2082.
8. Bickel P. J. Using residuals robustly I: Tests for heteroscedasticity, nonlinearity. Ann Statist. 1978;6(2):266–291.
9. Ramsey J. B. Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society. Series B (Statistical Methodology). 1968;31(2):350–371.
10. Carroll R. J., Ruppert D. On robust tests for heteroscedasticity. Ann Statist. 1981;9(1):206–210.
11. Breusch T. S., Pagan A. R. A simple test for heteroscedasticity and random coeffi cient variation. Econometrica. 1979;47(5):1287–1294.
12. Cook R. D., Weisberg S. Diagnostics for heteroscedasticity in regression. Biometrika. 1983;70(1):1–10.
13. Evans M. A., King M. A point optimal test for heteroscedastic disturbances. Journal of Econometrics. 1985;27(2):163–178.
14. Goldfeld S. M., Quandt R. E. Some tests for homoscedasticity. Journal of the American Statistical Association. 1965;60(310):539–547.
15. Harrison M. J., McCabe B. P. M. A test for heteroscedasticity based on ordinary least squares residuals. Journal of the American Statistical Association. 1979;74(366a):494–499.
16. Horn P. Heteroscedasticity of residuals: A non-parametric alternative to the Goldfeld‒Quandt peak test. Communications in Statistics ‒ Theory and Methods. 1981;10(8):795–808.
17. Simonoff J. S., Tsai C.-L. Use of modified profile likelihood for improved tests of constancy of variance in regression. Appl Statist. 1994;43(2):357–370.
18. Verbyla A. P. Modelling variance heterogeneity: Residual maximum likelihood and diagnostics. Journal of the Royal Statistical Society. Series B (Methodological). 1993;55(2):493–508.
19. White H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica. 1980;48(4):817–838.
20. Wilcox R. R., Keselman H. J. Detecting heteroscedasticity in a simple regression model via quantile regression slopes. Journal of Statistical Computation and Simulation. 2006;76(8):705–712.
21. Yuce M. An asymptotic test for the detection of heteroscedasticity. Istanbul University Econometrics and Statistics e-Journal. 2008;8:33–44.
22. Zhou Q. M., Song P. X.-K., Thompson M. E. Profiling heteroscedasticity in linear regression models. Canadian Journal of Statistics. 2015;43(3):358–377.
Об авторе
А. Д. ЧеремухинРоссия
кандидат экономических наук, доцент
Рецензия
Для цитирования:
Черемухин А.Д. ОЦЕНКА ЭФФЕКТИВНОСТИ ТЕСТОВ ГЕТЕРОСКЕДАСТИЧНОСТИ. Вестник кибернетики. 2024;23(1):81-88. https://doi.org/10.35266/1999-7604-2024-1-11
For citation:
Cheremukhin A.D. EVALUATING EFFECTIVENESS OF TESTS FOR HETEROSCEDASTICITY. Proceedings in Cybernetics. 2024;23(1):81-88. (In Russ.) https://doi.org/10.35266/1999-7604-2024-1-11















