МЕТОД ОЦЕНИВАНИЯ ЛОГИСТИЧЕСКИХ РЕГРЕССИЙ С ПОМОЩЬЮ АППАРАТА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ВВЕДЕНИЕ

В современных технологиях машинного обучения [1–3] актуальными и широко применяемыми считаются задачи классификации, решение которых заключается в построении алгоритмов, способных автоматически разделять некоторые имеющиеся объекты или ситуации на классы. Например, задача классификации спама в электронной почте, состоящая в автоматическом определении по таким факторам, как текст письма, адрес отправителя, наличие ссылок и т. д., является ли письмо спамом или нет. Задача классификации клиента в банке с целью выдачи ему кредита в зависимости от его дохода, семейного положения, кредитной истории, возраста и т. д. Важную роль задачи классификации играют в обеспечении информационной безопасности предприятий, поскольку правильная классификация киберугрозы является залогом успеха в ее противодействии [4].

Если для классификации имеется только два класса объектов, то целесообразно перей­ти к оцениванию модели бинарного выбора [5][6] следующего вида:

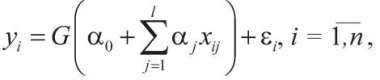(1)

где n – объем выборки;

l – число объясняющих переменных;

x_ij – i-е значение j-й объясняющей переменной;

y_i ∈ {0,1} – i-е значение бинарной объясняемой переменной;

ε_i – i-я ошибка аппроксимации;

α₀, α₁, ..., α_l – неизвестные параметры;

G(z) – некоторая вещественная функция от аргумента z.

При логистическом распределении функция 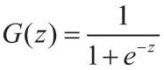(сигмоида), поэтому модель (1) принимает вид:

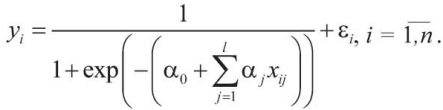(2)

Модель (2) называется логистической регрессией (логит-моделью).

Логистические регрессии применяются в различных сферах человеческой деятельности. Так, например, в [7] построена логистическая регрессия для прогнозирования летальности в отделении интенсивной терапии, в [8] – для вычисления повреждаемости твердого деформируемого тела, в [9] – для прогнозирования использования населением портала государственных услуг.

Поскольку все расчетные значения объясняемой переменной y, полученные с помощью оцененной логит-модели (2), всегда попадают в промежуток от 0 до 1, то их отождествляют с вероятностями. Если эта вероятность больше 0,5, то объект или ситуация соответствует классу № 1, а если меньше 0,5 – классу № 2.

К сожалению, логистические регрессии являются нелинейными по неизвестным параметрам, поэтому для их оценивания нельзя использовать простые методы наименьших квадратов или модулей. Вместо них применяется метод максимального правдоподобия (ММП) [10][11]. Алгоритмы ММП реализованы во многих современных статистических пакетах, например в Gretl. Однако в случае полной разделимости объектов или ситуаций на два класса ММП-оцен­ки логистической регрессии не единственны. На устранение данного недостатка направлено данное исследование.

Цель работы состоит в разработке простого метода оценивания логистических регрессий, способного работать даже в условиях абсолютной классификации объектов.

МАТЕРИАЛЫ И МЕТОДЫ

Аппарат математического программирования [12][13] активно применяется в настоящее время в научных исследованиях для решения самых разных прикладных задач. Также он находит применение в регрессионном анализе (см., например, [14–17]).

Сигмоида 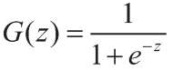устроена так, что при z = 0 функция G = ½, поэтому классифицировать объекты в этой точке, вообще говоря, невозможно. Если z > 0, то G > ½, поэтому объекты относятся к первому классу. Если же z < 0, то G < ½, поэтому объекты относятся ко второму классу. Из этого следует, что для классификации требуется подобрать неизвестные параметры α₀, α₁, ..., α_l значений аргументов сигмоиды:

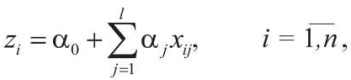(3)

так, чтобы выполнялись следующие условия:

z_i > 0, i ∈ I₁, (4)

z_i < 0, i ∈ I₀, (5)

где I₀ = {i | y_i = 0}, I₁ = {i | y_i = 1}.

Неравенства в условиях (4), (5) строгие, поэтому их нельзя задействовать в задаче линейного программирования (ЛП). Тогда придадим им нестрогий вид:

z_i ≥ 0, i ∈ I₁, (6)

z_i ≤ 0, i ∈ I₀. (7)

Условия (6), (7) означают, что если в результате оценивания z_i = 0, то классифицировать объект невозможно. Поэтому заменим их следующими соотношениями:

z_i ≥ r, i ∈ I₁, (8)

z_i ≤ –r, i ∈ I₀ , (9)

где r – заданное исследователем положительное число.

Если область решений системы линейных неравенств (3), (8) и (9) непустое множество, то возможна полная разделимость объектов на два класса. На практике же такое может происходить нечасто, поэтому введем ошибки классификации:

u_i ≥ 0, i = 1,n. (10)

Если i-й объект классифицирован верно, то u_i = 0. Учитывая это, условия (8), (9) нужно переписать в виде:

z_i ≥ r – u_i, i ∈ I₁, (11)

z_i ≤ –r + u_i, i ∈ I₀ . (12)

Сумма ошибок, естественным образом, должна быть минимальной, т. е.

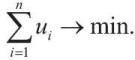(13)

Тогда решение задачи ЛП с целевой функцией (13) и линейными ограничениями (3), (10)–(12) позволяет найти такие значения параметров α₀, α₁, ..., α_l, при которых сумма ошибок классификации минимальна.

Заметим, что подобную формулировку задачи ЛП можно встретить в других ранее опубликованных научных статьях, посвященных инструментам оценки кредитоспособности заемщиков. Так, в работе [18], датированной 2012 г., при анализе методов классификации приведена следующая задача ЛП:

α₁ + α₂ + ... + α_ng+nb → min,

w₁x_i1 + w₂x_i2 + ... + w_px_ip ≥ c – a_i, 1 ≤ i ≤ ng,

w₁x_i1 + w₂x_i2 + ... + w_px_ip ≤ c – a_i,

ng + 1 ≤ i ≤ ng + nb,

a_i ≥ 0, 1 ≤ i ≤ ng + nb,

где ng – количество «хороших» заемщиков;

nb – количество «плохих» заемщиков;

x_ip – ответ i-го заемщика на p-й вопрос анкеты;

с – заданная граница, отделяющая «плохого» заемщика от «хорошего»;

α_i – i-я ошибка классификации;

w₁, ..., w_p – неизвестные веса.

Точно такую же постановку можно найти в зарубежной статье [19], опубликованной и вовсе в 2000 г. Там же отмечено, что модели ЛП для решения проблемы классификации были предложены еще в 1981 г. в работе [20]. Однако если в этой задаче взять c = 0, то ее решением всегда будут нулевые веса и нулевые ошибки классификации. В сформулированной нами задаче ЛП (3), (10)–(13) такая особенность за счет введения числа r исключена.

Выясним, как влияет выбор параметра r на результаты решения задачи ЛП (3), (10)–(13). Пусть при r = r* эта задача имеет оптимальное решение a₀ = a₀*, a₁ = a₁*, ..., a_l = a_l*, u₁ = u₁*, ..., u_n = u_n*, z₁ = z₁*, …, z_n = z_n*. Увеличим значение параметра r в k > 0 раз, т. е. примем r = k × r*. Поделим все ограничения и целевую функцию в задаче ЛП на k. Тогда она принимает вид:

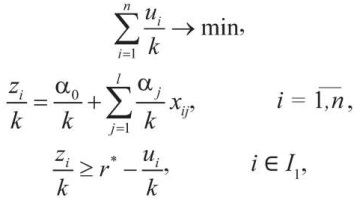
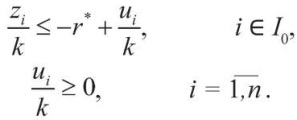
Эта задача имеет оптимальное решение

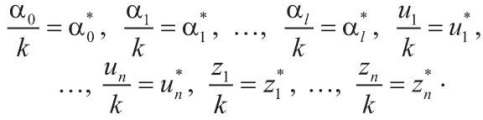
Отсюда следует, что при увеличении параметра r в k > 0 раз оптимальные значения всех переменных увеличатся также в k раз. Таким образом, если упорядочить оптимальные значения переменных z₁, …, z_n, найденные при r = r*, по возрастанию, то при r = k × r* эти значения увеличатся в k раз, но порядок их следования сохранится. Используем далее это свойство для проведения калибровки масштаба вероятностей.

После решения задачи ЛП (3), (10)–(13) вероятности отнесения объектов к одному из двух классов находятся по формуле:

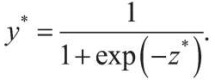
Из-за того что значение параметра r в задаче ЛП выбирается произвольно, эти вероятности могут принимать непредсказуемые значения, например, они все могут быть очень близки к 0,5. В таком случае необходимо провести калибровку масштаба вероятностей, оценив неизвестный параметр β в следующей регрессионной модели:

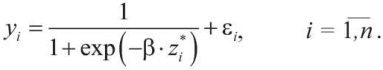(14)

К сожалению, регрессия (14) является нелинейной по неизвестному параметру. Поэтому калибровку масштаба вероятностей при 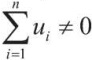проще осуществить по следующему алгоритму.

Шаг 1. Назначить близкое к единице число Δ. Например, Δ = 0,99, Δ = 0,999 или Δ = 0,9999.

Шаг 2. Если |z_min| < |z_max|, где z_min = min{z^*₁, z^*₂, ..., z^*_n»}, z_max= max{z^*₁, z^*₂, ..., z^*_n»}, то найти неизвестный параметр β регрессии (14) из уравнения:

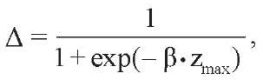
откуда

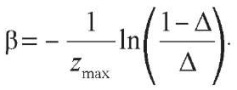
Шаг 3. Если |z_min| > |z_max|, то найти неизвестный параметр β из уравнения:

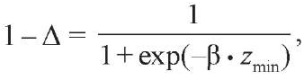
откуда

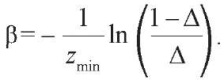
Пусть при r = r* оптимальные значения параметров z_i = z_i*, i = 1,n, а при r = k × r* – z_i = k × z_i*, i = 1,n. Если |z_min| > |z_max|, то при r = r* величина

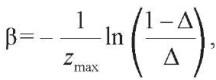
а при r = k × r* –

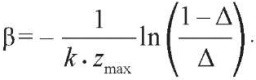
В обоих случаях уравнение

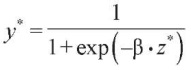
будет одинаковым. Из этого следует, что для любого r калибровка масштаба вероятностей приводит к единственному уравнению.

Пусть при решении задачи ЛП (3), (10)– (13) значение целевой функции 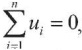т. е. имеет место полная разделимость объектов на два класса. Очевидно, что в такой ситуации задача ЛП имеет не единственное решение, поэтому и калибровка масштаба вероятностей может давать разные результаты. Поэтому для такого случая вместо представленного трехшагового алгоритма следует решить задачу ЛП с целевой функцией:

r → max, (15)

с линейными ограничениями (3) и

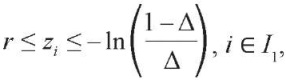(16)

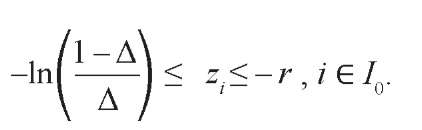(17)

Особенность нового метода оценивания логистических регрессий с помощью аппарата ЛП в том, что вероятности y^*_i, i = 1,n , всегда попадают в диапазон 1 – Δ ≤ y^*_i ≤ Δ.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Для демонстрации работы предложенного математического аппарата были использованы статистические данные из книги [21]. Бинарная переменная y равна 1, если сотрудник имеет право бесплатного доступа в Интернет, 0 – в противном случае. Объясняющие переменные: x₁ – возраст сотрудника, x₂ – стаж профессиональной деятельности, x₃ – заработная плата, x₄ – число случаев поступления полезной для фирмы информации от сотрудника, x₅ – результат тестирования на предмет оценки навыков работы в Интернете. Общий объем выборки составил 100.

ММП-оценивание логистических регрессий проводилось с использованием эконометрического пакета Gretl, для решения задач ЛП применялся пакет LPSolve IDE.

Эксперимент № 1 (использовались первые 20 наблюдений выборки).

Исходные статистические данные представлены в таблице.

В Gretl была зафиксирована ошибка «Получен идеальный прогноз: MLE не существует». Это связано с тем, что имеет место полная разделимость объектов на два класса, поэтому единственных ММП-оценок логистической регрессии не существует.

В LPSolve задача ЛП (3), (10)–(13) была решена при r = 0,01. Все ошибки классификации оказались равны 0. Поэтому для калибровки масштаба вероятностей была решена задача ЛП (3), (15)–(17) при Δ = 0,999. Оцененная логистическая регрессия имеет вид:

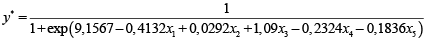(18)

Найденные по модели (18) вероятности представлены в последнем столбце таблицы. Как видно, абсолютно все объекты классифицированы корректно.

Эксперимент № 2 (использовались все 100 наблюдений выборки).

Оцененная по этим данным в Gretl с помощью ММП логистическая регрессия имеет вид:

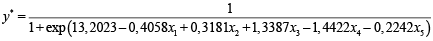(19)

Модель (19) корректно классифицирует 96 объектов, за исключением наблюдений под номерами 3, 6, 28 и 48.

В LPSolve при r = 0,01 была найдена следующая зависимость переменной z* от объясняющих переменных:

(20)

Для калибровки масштаба вероятностей было назначено Δ = 0,999. Установлено, что z_min = –0,08587, z_max = 0,081072. Поскольку |z_min| > |z_max|, то оценка параметра β определялась по формуле:

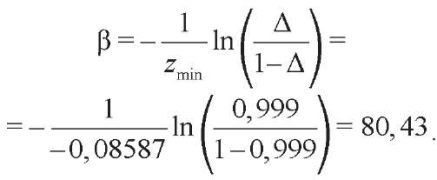
С учетом (20) оцененная логистическая регрессия имеет вид:

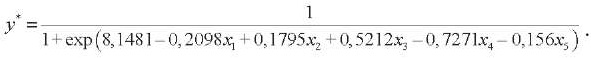(21)

Модель (21) корректно классифицирует те же 96 объектов, что и модель (19). Но весовые коэффициенты этих регрессий различаются.

Та же самая модель (21) была получена при r = 100, что подтверждает корректность приведенных в данной работе математических выводов.

Эксперимент № 3 (использовались все 100 наблюдений выборки, но в первых пятидесяти из них значения объясняемой переменной были выбраны 0, а в последних пятидесяти – 1).

Оцененная по этим данным в Gretl с помощью ММП логистическая регрессия имеет вид:

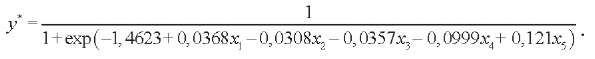(22)

Модель (22) корректно классифицирует 52 объекта.

Оцененная новым методом при r = 0,01 и Δ = 0,999 логит-модель имеет вид:

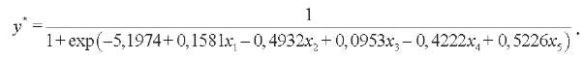(23)

Модель (23) корректно классифицирует 56 объектов. Таким образом, в этом эксперименте результаты классификации новым методом оказались лучше, чем при использовании ММП.

ЗАКЛЮЧЕНИЕ

В данной работе предложен новый метод оценивания неизвестных параметров логистических регрессий, в основе которого – решение специальным образом сформулированной задачи ЛП. В результате ее решения определяются неизвестные весовые коэффициенты гиперплоскости, разделяющей объекты двух различных классов, т. е. осуществляется классификация. Показано, чем предложенная задача отличается от подобных задач ЛП. Доказана однородность сформулированной задачи ЛП. На основе этого разработан алгоритм калибровки масштаба вероятностей в логистической регрессии. На реальных данных проведены вычислительные эксперименты. Показано, что новый метод, в отличие от ММП, работает даже в случае полной разделимости объектов на два класса. По количеству корректно предсказанных случаев новый метод ни разу не уступил ММП, а в одном из экспериментов и вовсе превзошел его.