СПОСОБ ФОРМИРОВАНИЯ ОРТОГОНАЛЬНЫХ ПРИЗНАКОВ РАСПОЗНАВАНИЯ ОБЪЕКТОВ НА ПЛОСКИХ ИЗОБРАЖЕНИЯХ

ВВЕДЕНИЕ

Современные системы очувствления роботов предполагают наличие элементов технического зрения, способных обеспечить прием и обработку информации о свойствах объектов распознавания, в первую очередь об их форме, размерах и ориентации. Зная эти свойства, можно идентифицировать объекты текущего изображения с некоторым эталоном, находящимся в памяти ЭВМ.

Для более сложных систем технического зрения помимо текстурных признаков, описывающих структуру видимой поверхности объекта, применяются признаки для различения объектов по цвету, а также геометрические признаки, учитывающие не только форму объекта, но и его пространственное положение.

Одним из ключевых элементов систем технического зрения (СТЗ) является алгоритм сегментации изображения, который позволяет выделить объекты на фоне изображения и определить их границы [1]. Для этого используются различные методы обработки изображений, в том числе фильтрация, морфологические операции, выделение краев и др.

Для увеличения эффективности распознавания объектов в СТЗ в последнее время все чаще применяются методы машинного обучения, нейронные сети, метод опорных векторов, алгоритмы кластеризации и др. Эти методы позволяют повысить точность и скорость работы системы при обучении на большом объеме данных.

Таким образом, современные системы технического зрения роботов используют разнообразные признаки и методы обработки изображений для распознавания объектов и выполнения различных задач в автоматизированных процессах. Рассмотрим разработанную авторами методику, обладающую, на наш взгляд, несколько большими возможностями и универсальностью.

МАТЕРИАЛЫ И МЕТОДЫ

Система технического зрения (СТЗ) простейших роботов-манипуляторов использует метрические признаки, известные из интегральной геометрии [1]: удлиненность объекта 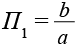, сложность контура 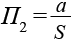, компактность фигуры 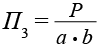, моменты инерции относительно осей и т. д. (P – площадь; S – периметр; a – наибольшее сечение объекта; b – наибольшее сечение из перпендикулярных сечению a). Роботы же, ориентированные на решение широкого круга задач и обладающие высоким уровнем искусственного интеллекта, нуждаются в более развитой, более универсальной системе признаков распознавания.

Одной из эвристик, которая применяется для контурной идентификации объектов, является использование оператора Собеля для выделения границ объектов на изображении. Этот оператор позволяет выделить различные уровни контрастности и изменений яркости, что, в свою очередь, помогает выявить контуры объектов.

Другой эвристикой является использование алгоритмов машинного обучения для классификации контуров объектов. На основе набора обучающих данных, таких как изображения с контурами различных объектов, модель может быть обучена распознавать и идентифицировать контуры объектов на новых изображениях.

Авторами используется собственная эвристика, основанная на использовании кодов Фримена, применительно к клеточным автоматам на плоскости [2][3].

Интеграция этих и других эвристик в процесс анализа изображений позволяет повысить эффективность и точность идентификации объектов, явлений и ситуаций. Тем самым, развитие технологий интеллектуального анализа данных значительно улучшает возможности применения систем технического зрения в различных областях, от медицины и автопрома до робототехники и безопасности [4].

Методология

Остановимся на таком подходе к формированию признаков, который бы обеспечил сохранение в них информации о форме распознаваемых контуров как едином целом, в первую очередь с учетом взаимосвязи координат соседних точек контура. Такой подход получил не только официальное признание [5], но и показал свою эффективность на практике [6].

Пусть средствами предварительной обработки выделен замкнутый контур объекта на двумерном изображении, то есть задана упорядоченная совокупность координат {x_i; y_i} точек a_i, i = 1,n, контура, где N – количество точек контура. Выбирается начальная точка контура по какому-либо правилу, например:

.

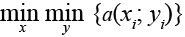Направление движения по контуру справа от объекта примем за положительное и представим контурную линию параметрически:

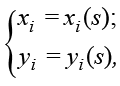
где s – расстояние по контуру от начальной точки до i-й.

Для изображения, задаваемого на прямоугольном растре, любая контурная линия является решением линейного дифференциального уравнения порядка не выше n < ∞. В работе [7] для этого случая было доказано, что для сохранения полной информации о форме контура достаточно не более чем по (n + 1)-му коэффициенту разложения в ряд ортогональных экспоненциальных функций для x = x (s) и y = y (s).

Базисные ортоэкспоненциальные функции задаются выражением:

,

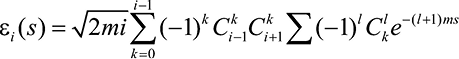где m ∈ (0,1) – масштабный коэффициент.

Если обозначить

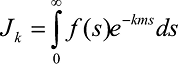, то коэффициенты разложения будут вычисляться по формулам [1]:

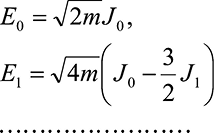
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Учитывая, что аппаратное вычисление коэффициентов ортогонального разложения {E_i} проблем в настоящее время не представляет [3], переход {J_k} ←{E_i} также вполне разрешимая задача.

Обратив внимание на то, что:

,

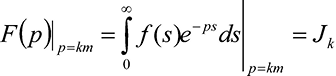и обозначив f₁ (s) = x (s); f₂ (s) = y (s); f₃ (s) = x (S-s); f₄ (s) = y (S-s), где x (S-s); y (S-s) – «зеркальные» функции; S – длина контура, можно образовать матрицу формы контура:

.

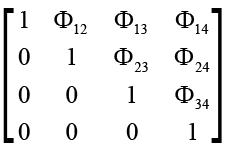При этом Ф_ij характеризует связность точек контура. Вещественные сечения некоторых элементов матрицы формы (Ф₁₃; Ф₂₄) были исследованы ранее в работе [3] и получили название экспоненциальных коэффициентов формы.

Отметим два полезных свойства элементов матрицы формы:

1) в силу того, что все f_i (s) периодические, с одним периодом S:

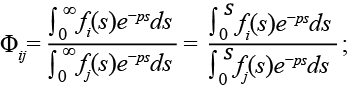
2) Ф₁₂ и Ф₃₄ инвариантны к выбор начальной точки контура, а следовательно, и к повороту объекта на текущем изображении.

Приведем примеры вычисленных инвариантных комплексных значений элементов матрицы формы для контуров правильных геометрических фигур:

– квадрат со стороной a: Ф₁₂ = е^–ap;

– окружность:

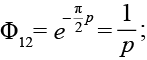
– эллипс с осями a и b:

.

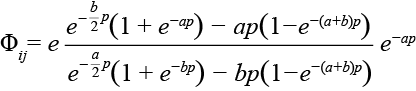Элементы матрицы для фигур произвольной формы, равно как и их проекции на действительную ось, сохраняют свойства 1 и 2.

Анализируя вид выражений для Ф₁₂ контуров различных фигур, следует отметить, что некоторые признаки, полученные другими, например эвристическими, опытными методами [1][7] (признаки П₁, П₂), входят в качестве компонентов для выражения элементов матрицы формы. Тем самым теоретически доказывается правомерность их практического использования, по меньшей мере в качестве признаков первого уровня иерархической системы распознавания.

ЗАКЛЮЧЕНИЕ

Способ описывает порядок формирования ортогональных признаков для распознавания объектов на плоских изображениях. Основные шаги способа включают [7]:

1. Описание контура объекта: имеется замкнутый контур объекта, который параметрически описывается по его координатам на плоскости.
2. Параметризацию контура: координаты контура представляются в виде функций расстояния от фиксированной точки (например, начала координат) вдоль контура объекта, это позволяет учесть форму и структуру объекта.
3. Разложение функций расстояния в ряд: полученные функции расстояния разлагаются в ряды по ортогональным полиномам. Ортогональные полиномы – это функции, которые ортогональны друг другу на определенном интервале с некоторым весом. С учетом того, что исследуемые объекты описываются замкнутыми контурами, параметрические описания – периодические функции, следовательно, пределы интегрирования могут быть заданы от нуля до значения, равного длине контура. Это существенно упрощает вычислительные процедуры.
4. Формирование признаков идентификации: коэффициенты разложения функций расстояния в ряды по ортогональным полиномам могут сами использоваться как признаки для идентификации объектов. Комбинации отношений этих коэффициентов также могут образовывать признаки второго уровня, в том числе формируемые в матрицы, которые в ряде практических случаев весьма эффективны [4][8].

Такой подход позволяет учитывать как геометрические, так и структурные особенности объектов при их распознавании на изображениях.