Перейти к:
Математическая модель нагрева теплоносителя в топочной и конвективной камере
https://doi.org/10.35266/1999-7604-2024-4-10
Аннотация
В статье рассматривалась задача создания компоненты математической процесса нагрева теплоносителя модели водогрейного котла КВГМ. Для решения поставленной задачи использовался аналитический подход для построения модели, что свело к минимуму использование эмпирических коэффициентов в расчетной схеме. Составлена оригинальная аналитическая модель нагрева теплоносителя в топочной и конвективной камере (учитывается радиационное излучение тепла по закону Стефана – Больцмана). Созданную математическую модель предполагается использовать в качестве необходимой компоненты компьютерного тренажера.
Ключевые слова
Для цитирования:
Золотарева Н.С., Брагинский М.Я., Тараканов Д.В., Назарова И.Л. Математическая модель нагрева теплоносителя в топочной и конвективной камере. Вестник кибернетики. 2024;23(4):100-109. https://doi.org/10.35266/1999-7604-2024-4-10
For citation:
Zolotareva N.S., Braginsky M.Ya., Tarakanov D.V., Nazarova I.L. Mathematical model of transfer medium heating in furnace and convection chamber Natalya. Proceedings in Cybernetics. 2024;23(4):100-109. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-10
ВВЕДЕНИЕ
Математическая модель процессов теплообмена в котлах большой мощности является основой для программного обеспечения компьютерной техники с целью решения следующих задач:
- Автоматизированное (в той или иной степени) управление технологическим процессом.
- Создание компьютерных тренажеров для обучения обслуживающего персонала.
При этом основной целью математической модели является описание работы водогрейного котла в режимах, отличных от номинальных, то есть режимов максимально допустимых параметров. Для которых имеются паспортные данные, основанные на экспериментальных данных, а также описание переходных процессов, когда производится смена одного стационарного режима работы на другой стационарный режим. Описание нестационарных режимов имеет большое практическое значение при автоматизированном управлении котлами, а также при создании тренажеров для обучения персонала в режиме реального масштабного времени.
Имеется большое количество теоретических и экспериментальных работ по исследованию и моделированию процессов теплообмена в водогрейных котлах [1–8], однако результатов этих работ недостаточно для непосредственного составления программного обеспечения с целью решения вышеперечисленных задач по следующим причинам.
- В основном в этих работах рассматриваются стационарные режимы работы котла. Работ, в которых бы рассматривались нестационарные режимы, не так много, и в них не даются замкнутые модели нестационарных режимов работы котла.
- Значительная часть работ описывает отдельные части общего процесса работ котла, а те работы, которые претендуют на комплексное описание всего процесса теплообмена, неудобны при создании соответствующего программного обеспечения и имеют недостаток: они скомпонованы из различных частей, имеющих разную методологическую основу и разное соотношение в описании теплофизических и механических эффектов первого и второго порядка малости. Поэтому еще одна цель представляемой математической модели состоит в создании единой методологической базы для описания процессов теплообмена в водогрейных котлах.
- Каждая часть имеющихся расчетных комплексов содержит большой набор эмпирических коэффициентов, полученных при определенных условиях и ограничениях. Включение этих частей в единый расчетный комплекс без надлежащего согласования ограничений, накладываемых на использование эмпирических коэффициентов может привести к снижению достоверности расчетного комплекса в целом.
Кроме того, обилие эмпирических коэффициентов, вложенных в программное обеспечение, создает проблему среди пользователей, вызванную необходимостью восстановления их численных значений для конкретных расчетных режимов. Это существенно усложняет процедуру использования программного обеспечения и повышает риск введения ошибочных значений параметров в расчетные схемы, требует неоправданно высокой квалификации у пользователей программным продуктом. Поэтому при соответствии математической модели работы котла преследовалась еще и цель сведения к минимуму эмпирических коэффициентов в расчетной схеме и использовании в основном либо паспортных данных котла, либо стандартных теплофизических характеристик, имеющихся в справочниках и полученных с достаточной достоверностью.
Представленная математическая модель является завершенной в той степени, в которой она претендует на решение поставленных задач, однако эта модель допускает усложнение и совершенствование с учетом добавочных факторов, которые носят характер эффектов второго порядка малости. То есть представляемая модель является завершаемой математической моделью в первом приближении.
Учет эффектов второго порядка малости привел бы к необходимости более детальной привязки математической модели к реальным конструкциям котлов одного и того же типа. Это неоправданно усложнило бы саму математическую модель, с одной стороны, при отсутствии реальной адекватной экспериментальной информации связанной с различными режимами работы конкретного котла и особенно переходных процессов не вызвало бы повышения достоверности.
МАТЕРИАЛЫ И МЕТОДЫ
В математической модели рассматривается приведенная эквивалентная схема расположения теплообменных трубок, состоящая из некоторого количества эквивалентных слоев труб. Причем каждый эквивалентный слой трубы не обязательно соответствует одному реальному слою труб, а может соответствовать двум и более реальным слоям труб. В эквивалентной схеме рассматриваются два режима течения воды: сверху вниз и снизу вверх, как показано на рис. 1 и 2.
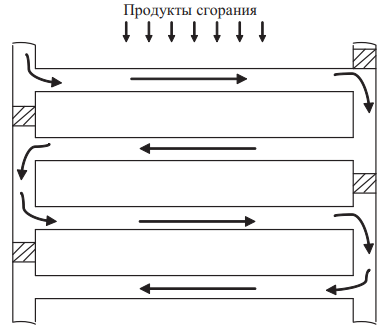
Рис. 1. Режим течения воды сверху вниз
Примечание: составлено авторами.
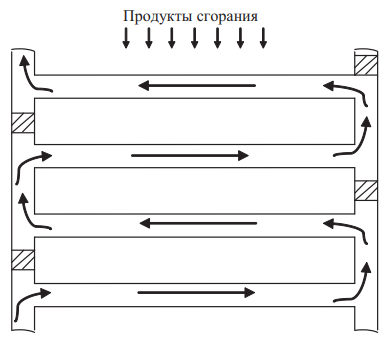
Рис. 2. Режим течения воды снизу вверх
Примечание: составлено авторами.
Под эквивалентным приведенным слоем труб понимается горизонтальный слой труб, через который проходит вся нагреваемая вода, а общая поверхность труб во всех эквивалентных слоях соответствует реальной поверхности всех теплообменных труб в конвективной камере.
Пусть n – число труб в эквивалентном слое, mв– массовый расход воды, ρ0 – плотность воды, S1 – реальная площадь поверхности теплообменных труб в конвективной камере, V – реальная скорость воды в трубах пакета, a + Δa – внешний радиус труб, l – длина теплообменной трубы.
Тогда на основе определения эквивалентного приведенного слоя труб можно записать соотношения:
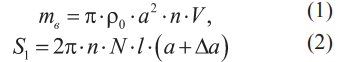
Этих двух соотношений достаточно для определения параметров n и N.
Для котла КВГМ 100 в основном режиме:
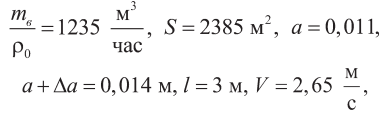
где V – скорость в первом пакете.
Подставляя эти данные в (1) и (2) и округляя их до целых чисел, получаем n = 340, N = 26.
Описание тепловых экранов в топочной камере также является упрощенным [1]. В действительности боковые экраны разбиты на секции: в одних секциях вода движется снизу вверх, а в других – сверху вниз. Высота боковых экранов, фронтового и промежуточного, неодинакова из-за наличия проемов для размещения горелок и проема соединяющую топочную конвективную камеры. Кроме того, включение всех труб в экране не является параллельным. Так, в основном режиме вода, поступая сначала во фронтовой экран, затем делится на две части и поступает в промежуточный экран. В пиковом режиме схема включения экранов другая. Детальное описание оформления в математической модели и конструктивного расположения теплообменных труб в топочной камере неоправданно усложняет саму модель, не приводя к значительным уточнениям интегральных параметров, характеризующих теплообмен в топочной камере. Поэтому реальная конструктивная схема радиационных экранов заменяется на эквивалентный приведенный радиационный экран, имеющий такую же воспринимающую радиационную поверхность Sp что и реальные экраны, и имеющий высоту, равную высоте боковых экранов. При этом предполагается, что вода поступает сразу во все трубы эквивалентного экрана и течет снизу вверх. Поэтому вводится эффективная средняя скорость Vэ в трубах, обеспечивающая такой же массовый расход воды, какой имеется в реальном экране. Эффективная скорость воды при этом получается примерно в два раза меньше реальной.
Предполагая, что тепловой поток, воспринимаемый эффективным экраном, равен тепловому потоку, воспринимаемому реальным экраном, и распределяется по высоте соответственно реальному распределению теплового потока на боковых экранах, найденному из эксперимента: пусть k – число труб в эквивалентном экране, Sp – воспринимающая радиационная поверхность, mв – массовый расход воды в номинальном режиме, ρ0 – плотность воды, a + Δa – внешний радиус труб, l – длина теплообменной трубы.
Тогда на основе определения эквивалентного экрана можно записать два соотношения:
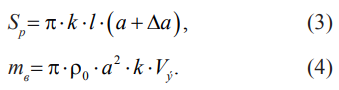
Из этих двух соотношений находится число труб k в эквивалентном экране и эффективная скорость жидкости Vэ .
Для котла КВГМ 100: Sp = 325 м2, mв = 343 кг/c, a + Δa = 0,031 м, l = 9,4 м.
Используя эти данные из (3), округляя до целых значений, находится величина k = 334. Из (4) эффективная средняя скорость в трубах топочной камеры Vэ = 0,33 м/c.
По найденному значению k и известному паспортному значению номинального теплового потока, воспринимаемому экраном qΣ, находится тепловой поток воспринимаемой одной трубой q0 (5):
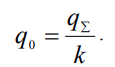 (5)
(5)
Так как
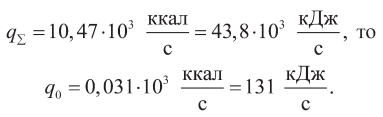
Пусть ω – отношение текущего расхода топлива в котле к номинальному, тогда предполагая, что тепловой поток, падающий на тепловой экран, равен тепловому потоку, падающему на экран в номинальном режиме, умноженному на величину ω. В этом случае:
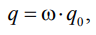
где q – тепловой поток, падающий на одну теплообменную трубу при текущем расходе топлива.
Переходные процессы в теплообменной трубе (освещенный сектор)
В этом случае нестационарные процессы теплообмена имеют характер переходных процессов от одного стационарного состояния без появления неустойчивости и незатухающих колебаний, если входные параметры меняются, асимптотически приближаясь к конечным, постоянным значениям при t → ∞.
В рассматриваемой работе есть два входных параметра: температура воды на входе T0(t) и относительный расход топлива ω(t) ((6) и (7)):
Введем следующие обозначения:
μ1 – теплопроводность железа;
K – температуропроводность железа;
σ0 – постоянная Больцмана;
Re – число Рейнольдса;
α0 – коэффициент черноты поверхности труб;
a – внутренний радиус теплообменных труб;
l – длина трубы;
t – время;
x, ξ – безразмерные цилиндрические координаты;
T – температура;
n – число труб в слое конвективной камере;
ω – отношение расхода горючего к номинальному расходу;
W – температура на оси труб;
ф(η) – функция распределения теплового потока по высоте топочной камеры;
η – безразмерная координата;
f(η, t) – температура на оси труб;
ε1 – безразмерный параметр;
T0 – температура воды на входе в теплообменные трубы;
k – число труб в эквивалентном экране топочной камеры.
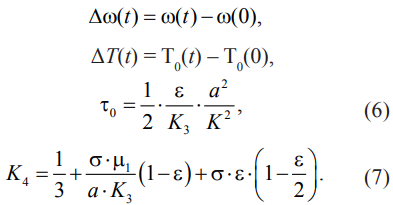
Тогда из уравнений (8), (9) с учетом (10)
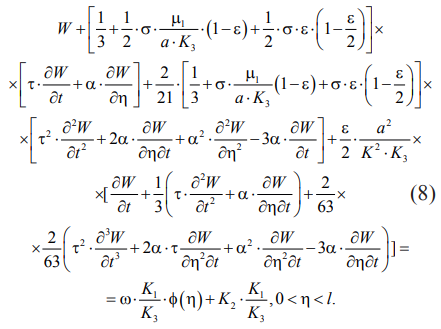
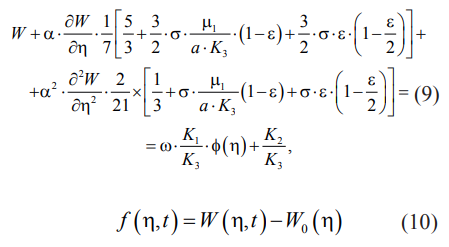
следует:
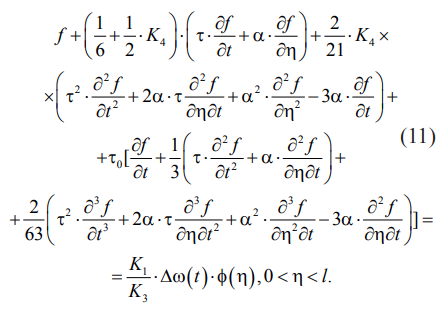
Краевые условия этого уравнения из (12), (13) принимают вид:
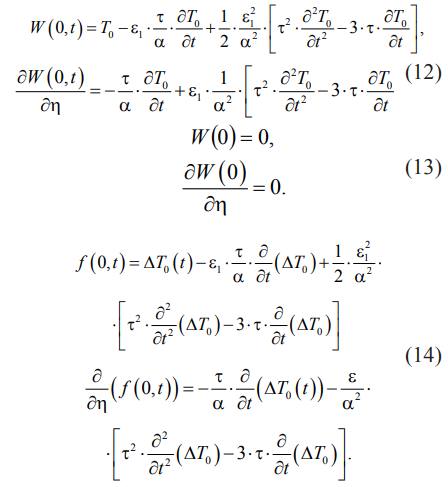
Сделаем преобразование Лапласа от соотношений (11), (14), выбрав конкретный вид функции Δω(t), ΔT0(t).
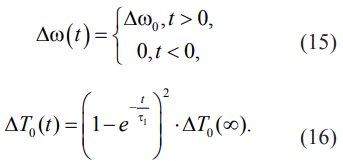
При этом получается (17)–(18):
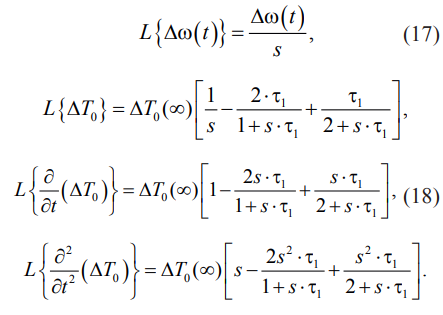
Преобразование Лапласа от уравнения (11) приводит к обыкновенному дифференциальному уравнению по переменной η:
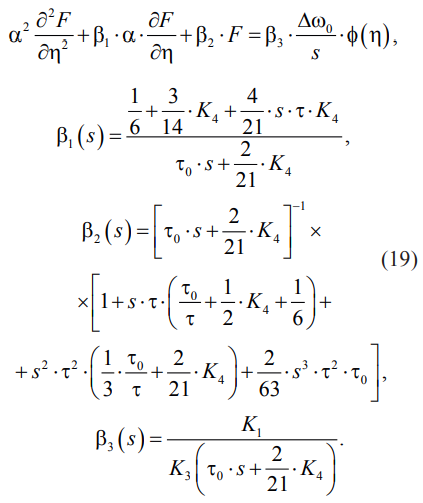
Преобразование Лапласа краевых условий (14) приводит к соотношениям (20)–(21):
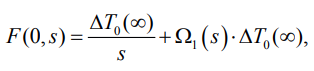
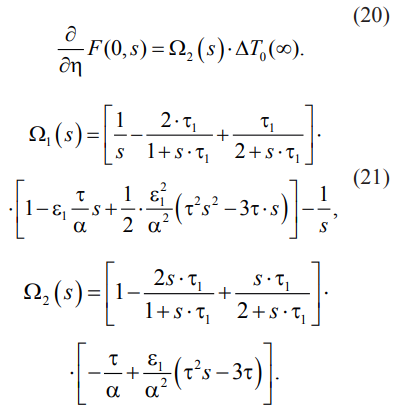
Частное решение уравнения (19) имеет вид (22)–(23):
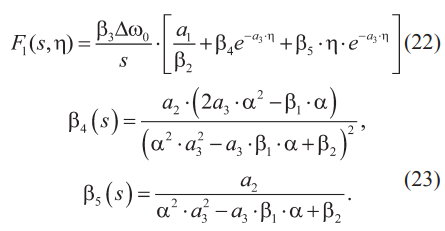
Общее решение однородного уравнения, полученного из (19), имеет вид:
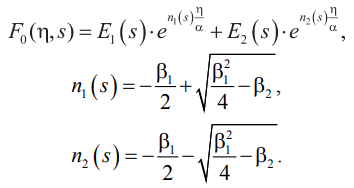
Тогда общее решение уравнения (19) получается в виде:
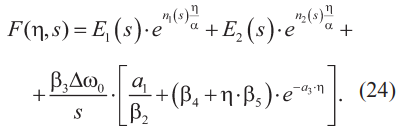
Постоянные E1 и E2, находятся из краевых условий (20), при этом получается система (25):
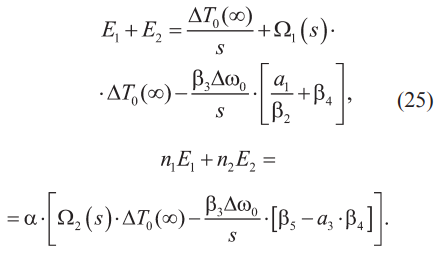
Разрешая эту систему, получим:
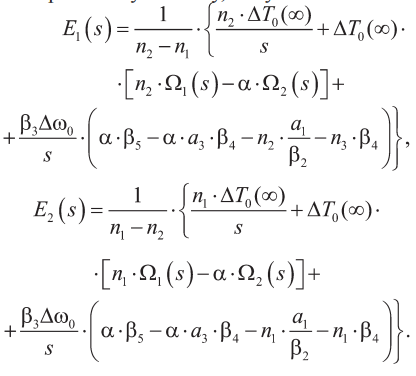
Оригинал от изображения (24) в аналитическом виде получить трудно, фактически его надо находить численно. Однако, используя только изображение (24), можно получить некоторые важные результаты, характеризующие качественное поведение решения краевой задачи (9), (13) и корректность самих уравнений этой задачи.
Под этим имеется в виду прежде всего существование следующего фактически приемлемого результата.
Если при t < 0 процесс был стационарным с параметрами ω(0), T0(0), а при t > 0 параметры ω(t), T0(t) начали изменяться, имея в пределе при t → ∞ постоянные предельные значения ω(∞), T0(∞), то решение краевой задачи (9), (13) при t → ∞ тоже должно асимптотически устанавливаться к стационарному решению с параметрами ω(∞), T0(∞).
То есть решение краевой задачи должно быть устойчивым и в нем должны существовать незатухающие колебания. В этом случае можно сказать, что решение краевой задачи (9), (13) описывает переходные процессы между двумя стационарными состояниями.
Поведение оригинала f(η, t) при t → ∞ можно оценить на основе известного предельного соотношения (26) [28]:
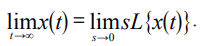 (26)
(26)
Таким образом, выполняется равенство:
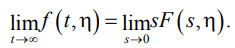 (27)
(27)
Для нахождения предела в правой части (27) запишем следующие предельные соотношения, которые проверяются непосредственно с использованием формул:
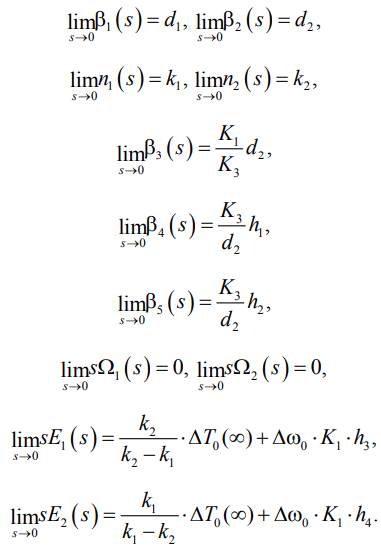
Пользуясь этими предельными соотношениями и (24), можно записать:
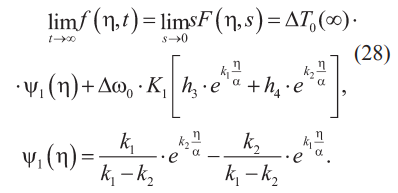
На основании (10) выполняется (29):
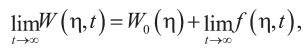 (29)
(29)
где W(η, t) – решение краевой задачи, а W0(η) – решение стационарной задачи (30), (13) при t < 0. Используя зависимость (31) для решения W0(η) и соотношение (28), получим (32):
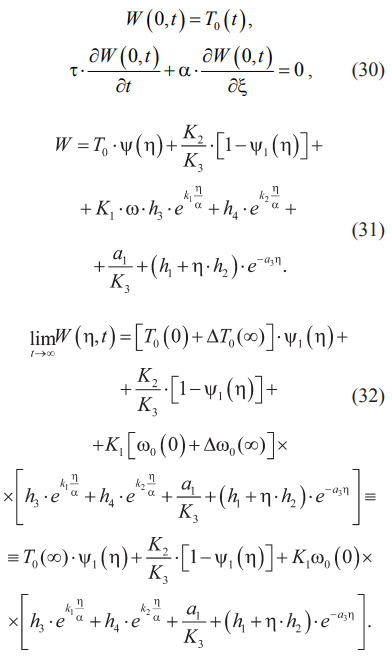
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Таким образом, решение W(η, t) нестационарной краевой задачи (9), (13), (15), (16) действительно характеризует переходной процесс, отделяющий два стационарных состояния, определяемых параметрами ω(0), T0(0), ω(∞), T0(∞).
Следует заметить, что этот результат не является тривиальным. Так, если в математической модели убрать слагаемые, характеризующие обратное излучение труб по закону Стефана – Больцмана, то получаемые при этом уравнения не будут описывать переходные процессы, так как в решении появятся составляющие, линейно растущие во времени.
Полученная модель обладает рядом достоинств по сравнению с существующими решениями:
- В основном в научных работах рассматриваются только стационарные режимы работы котла. В представленной работе рассматриваются переходные режимы работы. Решение сформулировано в виде замкнутой модели процесса нагрева котла.
- Значительная часть работ описывает отдельные части общего процесса работ котла, а те работы, которые претендуют на комплексное описание всего процесса теплообмена, неудобны и при создании соответствующего программного обеспечения имеют тот недостаток, что скомпонованы из различных частей, имеющих разную методологическую основу и разное соотношение в описании теплофизических процессов. Полученная математическая модель построена на единой методологической базе для описания процессов теплообмена в водогрейных котлах.
- Каждая часть имеющихся расчетных методов содержит большой набор эмпирических коэффициентов, полученных при определенных условиях и ограничениях. Включение этих эмпирических коэффициентов в единый расчетный комплекс без надлежащего согласования ограничений, накладываемых на использование данных параметров, может привести к снижению достоверности расчетного комплекса в целом.
Кроме того, обилие эмпирических коэффициентов, вложенных в программное обеспечение, создает проблему среди пользователей, вызванную необходимостью восстановления их численных значений для конкретных расчетных режимов. Это существенно усложняет процедуру использования программного обеспечения и повышает риск введения ошибочных значений параметров в расчетные схемы, требует неоправданно высокой квалификации у пользователей программным продуктом.
- Полученная математическая модель работы котла обладает минимумом эмпирических коэффициентов в расчетной схеме и использовании в основном либо паспортных данных котла, либо стандартных теплофизических характеристик, имеющихся в справочниках.
Представленная математическая модель является завершенной в той степени, в которой она претендует на решение поставленных задач, однако эта модель допускает усложнение и совершенствование с учетом добавочных факторов, которые носят характер эффектов второго порядка малости. То есть представляемая модель является завершаемой математической моделью в первом приближении.
- Учет эффектов второго порядка малости привел бы к необходимости более детальной привязки математической модели к реальным конструкциям котлов одного и того же типа. Это неоправданно усложнило бы саму математическую модель при отсутствии реальной адекватной экспериментальной информации, связанной с различными режимами работы конкретного котла и особенно переходных процессов.
ЗАКЛЮЧЕНИЕ
В представленной работе рассматривалась задача создания математической модели КВГМ 100. Составлена оригинальная аналитическая модель нагрева теплоносителя в топочной и конвективной камере. Полученные результаты моделирования могут быть использованы при создании компьютерных тренажеров для обучения обслуживающего персонала котельной КВГМ 100, а также в аналогичных энергетических системах (учитывается радиационное излучение тепла по закону Стефана – Больцмана).
Список литературы
1. Цапко Г. П., Цапко С. Г., Тараканов Д. В. Современные компьютерные тренажеры: математические методы моделирования и эмуляции параллельных взаимодействующих процессов : моногр. Томск : ТПУ, 2012. 192 с.
2. Володин Ю. Г., Ханнанов Р. Р. Математическое моделирование рабочего процесса в газовоздушном тракте котлового агрегата ТГМ-84 // Известия Казанского государственного архитектурно-строительного университета. 2016. № 2. С. 133–139.
3. Синицын Н. Н., Сидоров И. В., Игумнов Е. М. Расчетное исследование теплообмена в топках котлов КВГМ-30 и КВГМ-100 // Перспективное развитие науки, техники и технологий : материалы Междунар. науч.-практ. конф. 17 октября 2012 г., г. Курск. В 2 т. Курск : ЗАО «Университетская книга», 2012. Т. 2. С. 101–103.
4. Кайбалиев Р. С. Анализ водогрейного котла КВГМ- 50 как объекта управления // Наука и образование: сохраняя прошлое, создаём будущее : сб. статей XXV Междунар. науч.-практ. конф. 10 декабря 2019 г., г. Пенза. В 2 ч. Пенза : Изд-во: «Наука и Просвещение», 2019. Т. 1, ч. 1. С. 71–73.
5. Кайбалиев Р. С. Синтез системы автоматического регулирования водогрейного котла КВГМ-50 с добавочными информационными каналами // Наука и образование: сохраняя прошлое, создаём будущее : сб. статей XXV Междунар. науч.-практ. конф. 10 декабря 2019 г., г. Пенза. В 2 ч. Пенза : Изд-во: «Наука и Просвещение», 2019. Т. 1, ч. 1. С. 74–77.
6. Бутко Н. А., Кубисенов С. М., Мершиев А. Ю. Учебный тренажер имитации технологического процесса котла водогрейного КВГМ-50-150 // Нефть и газ – 2024 : материалы конф., 22–26 апреля 2024 г. Москва. М. : Российский государственный университет нефти и газа (национальный исследовательский университет) им. И. М. Губкина, 2024. С. 31–40.
7. Юсупова Д. С. Анализ процесса подогрева воды котла КВГМ-50 // Молодой исследователь: вызовы и перспективы : сб. статей по материалам CCXVI междунар. науч.-практ. конф., 14 июня 2021 г., г. Москва. М. : ООО «Интернаука», 2021. Т. 21. С. 392–394.
8. Садыков Р. А., Антропов Д. Н., Даминов А. З. и др. Автоматизированный микропроцессорный комплекс для моделирования процессов в котельной установке // Вестник машиностроения. 2015. № 12. С. 30–33.
Об авторах
Н. С. ЗолотареваРоссия
аспирант
М. Я. Брагинский
Россия
кандидат технических наук, доцент
Д. В. Тараканов
Россия
кандидат технических наук, доцент
И. Л. Назарова
Россия
аспирант
Рецензия
Для цитирования:
Золотарева Н.С., Брагинский М.Я., Тараканов Д.В., Назарова И.Л. Математическая модель нагрева теплоносителя в топочной и конвективной камере. Вестник кибернетики. 2024;23(4):100-109. https://doi.org/10.35266/1999-7604-2024-4-10
For citation:
Zolotareva N.S., Braginsky M.Ya., Tarakanov D.V., Nazarova I.L. Mathematical model of transfer medium heating in furnace and convection chamber Natalya. Proceedings in Cybernetics. 2024;23(4):100-109. (In Russ.) https://doi.org/10.35266/1999-7604-2024-4-10















