Перейти к:
Моделирование режимов работы асинхронного двигателя с учетом несимметрии напряжения питающей сети
https://doi.org/10.35266/1999-7604-2025-1-4
Аннотация
Асинхронные двигатели являются ключевыми элементами многих электроэнергетических систем, особенно систем электрификации технологических установок объектов нефтегазового комплекса. Повышение эффективности, надежности и безопасности работы асинхронных двигателей требует точного моделирования электромагнитных и механических процессов, особенно в условиях переходных режимов и при несимметрии питающего напряжения. В работе представлен обзор математической модели асинхронного двигателя с фазным ротором, разработанной на основе метода контурных токов для междуфазных напряжений. Модель учитывает влияние несимметрии напряжения питающей сети и позволяет исследовать переходные процессы, возникающие при различных режимах работы, включая пуск. Наличие качественной модели позволит спрогнозировать ресурс основных элементов машины и повысить качество работ по проведению диагностики неисправностей. В работе приведены результаты моделирования, выполнено сравнение с существующими моделями, показывающее эффективность предложенного метода.
Ключевые слова
Для цитирования:
Кислицин Е.Ю., Лукашов Д.С., Борисов И.Ю., Назаров А.А. Моделирование режимов работы асинхронного двигателя с учетом несимметрии напряжения питающей сети. Вестник кибернетики. 2025;24(1):26-30. https://doi.org/10.35266/1999-7604-2025-1-4
For citation:
Kislitcin E.Yu., Lukashov D.S., Borisov L.Yu., Nazarov A.A. Modeling of induction motor operation modes considering supply voltage asymmetry. Proceedings in Cybernetics. 2025;24(1):26-30. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-4
ВВЕДЕНИЕ
Асинхронные двигатели (АД) являются ключевыми компонентами промышленных электроприводов, широко используемыми в различных отраслях. Их надежность и эффективность имеют решающее значение для непрерывности и экономичности производственных процессов. Однако реальные условия эксплуатации, нередко характеризующиеся неидеальным качеством электроэнергии, нелинейностью магнитных цепей, оказывают существенное влияние на характеристики и срок службы АД. Поэтому проблема разработки адекватных математических моделей, способных учитывать эти факторы, остается актуальной задачей современной энергетики [1, 2].
Существующие методы моделирования АД, например, основанные на преобразованиях Парка-Горева, широко используются, но могут иметь ограничения при анализе сложных режимов работы и при необходимости непосредственного определения токов в обмотках статора и ротора [3]. Метод контурных токов предоставляет альтернативный подход, позволяющий более детально учитывать особенности электрической цепи двигателя и ее взаимодействие с питающей сетью [4].
В настоящей работе представлен обзор усовершенствованной математической модели АДФР на основе метода контурных токов для междуфазных напряжений.
Целью работы является разработка модели, адекватно описывающей переходные процессы при несимметричном напряжении питающей сети, а также при различных режимах работы, возникающих в процессе эксплуатации электрических машин. Наличие качественной модели позволит спрогнозировать ресурс основных элементов машины и повысить качество работ по проведению диагностики неисправностей.
МАТЕРИАЛЫ И МЕТОДЫ
В последние годы наблюдается растущий интерес к моделированию АД с использованием различных математических подходов. Разработка точных и надежных математических моделей необходима для оптимизации параметров и прогнозирования поведения АД в различных условиях эксплуатации. Различные подходы к моделированию АД, представленные в научной литературе, имеют свои преимущества и ограничения.
Многие исследования сосредоточены на создании моделей, способных адекватно описывать динамические режимы АД. Например, в работах А. В. Шестакова и соавт. представлена математическая модель, основанная на дифференциальных уравнениях в двухфазной ортогональной системе координат, учитывающая потери в железе, эффект вытеснения тока в стержнях ротора и насыщение магнитной цепи. Предложенная модель позволяет моделировать переходные процессы и обеспечивает удовлетворительную точность при сопоставлении с экспериментальными данными [1, 2].
Другое направление исследований связано с разработкой моделей для анализа специфических режимов работы АД. В работе A. V. Smolyaninov et al. рассмотрена система многомоторного частотно-каскадного электропривода, для которой получена динамическая модель и структурная схема АД с частотно-каскадным управлением [3]. В работе M. Y. Pustovetov предложена математическая модель трехфазного АД в системе отсчета трехфазного статора, позволяющая моделировать токи ротора на их фактической частоте [4].
Также актуальной задачей является моделирование АД в условиях несимметрии напряжения питающей сети. В статье А. С. Глазырина была разработана n-фазная имитационная модель АД для исследования обрыва стержня в беличьей клетке, позволяющая исследовать работу двигателя как в нормальном состоянии, так и при обрыве стержней [5].
Некоторые работы посвящены разработке более точных моделей АД с использованием метода конечных элементов (МКЭ) для учета нелинейности магнитопровода, скоса пазов ротора и индуктивности лобовых частей обмотки [6]. Такие модели позволяют более детально анализировать рабочие режимы АД и оптимизировать их конструкцию [6, 7].
Однако, несмотря на значительный прогресс в области моделирования АД, остаются нерешенные проблемы. Представленная работа направлена на разработку усовершенствованной математической модели АДФР на основе метода контурных токов, пригодной для анализа широкого спектра режимов работы и диагностики неисправностей.
Математическая модель
Предлагаемая модель АДФР основана на эквивалентной схеме замещения, где статор и ротор представлены в виде взаимосвязанных контуров (рис. 1).
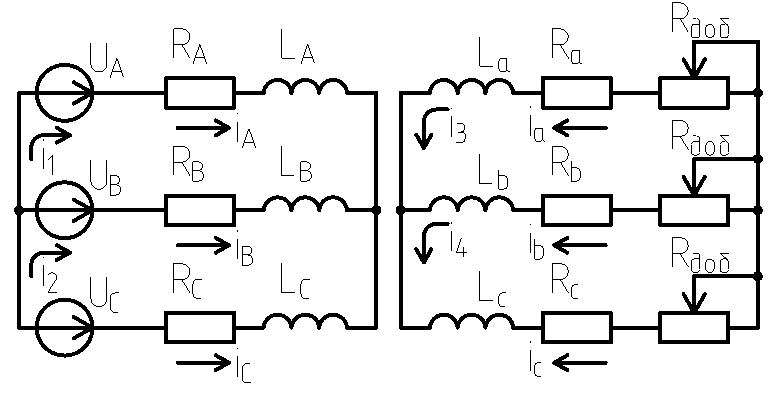
Рис. 1. Эквивалентная схема замещения АДФР с обозначением контурных токов, сопротивлений и индуктивностей
Примечание: составлено авторами.
Уравнения, описывающие электрическую часть модели, составляются на основе второго закона Кирхгофа для каждого контура. С учетом рис. 1 дифференциальные уравнения для междуфазных напряжений имеют вид (1):
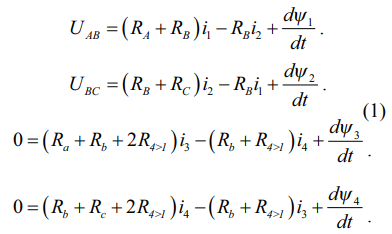
где UAB, UBС – мгновенные значения линейных напряжений;
i1, i2, i3, i4 – контурные токи;
i3, i4 – контурные токи ротора;
RA, RB, RC – активные сопротивления фаз статора;
Ra, Rb, Rc – активные сопротивления фаз статора;
Rдоб – добавочное сопротивление в роторной цепи;
Ψ1, Ψ2, Ψ3, Ψ4 – потокосцепления соответствующих контуров.
i1 = iA; i2 = –iC i2; i3 = ia. i4 = –iC.
Потокосцепления выражаются через контурные токи и индуктивности (2):
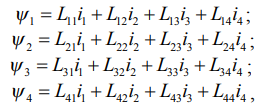 (2)
(2)
где L11–L44 – индуктивности обмоток.
Представленная математическая модель АДФР дает возможность моделировать не только эксплуатационные, но и аварийные режимы работы электрической машины. Так, при переходном процессе к рассматриваемой математической модели следует добавить уравнения электромагнитных моментов (3):
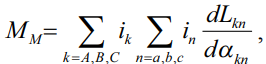 (3)
(3)
где Mэ – электромагнитный момент;
Mc – момент нагрузки.
При моделировании режима запуска АДФР в i-м контуре, ток определяется как сумма токов ini периодической и i0i апериодической составляющей:
ii = ini + i0i.
Модель механической части АД описывается уравнением (вращательное движение) (4):
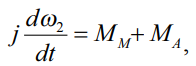 , (4)
, (4)
где j – момент инерции вращающихся частей двигателя и нагрузки;
ω2 – угловая скорость вращения ротора.
Система уравнений (1)–(4) решается численными методами (например, методом Рунге-Кутта) в среде MatLab/Simulink [8].
Сравнение результатов моделирования с экспериментальными данными, полученными для аналогичного двигателя, демонстрирует адекватность разработанной модели. Погрешность не превышает 10 %.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Представленная математическая модель АДФР на основе метода контурных токов обладает рядом преимуществ по сравнению с существующими моделями:
Во-первых, она позволяет непосредственно получать токи в обмотках статора и ротора, что важно для задач релейной защиты.
Во-вторых, модель позволяет учитывать влияние несимметрии напряжения питающей сети, что особенно актуально для современных электроэнергетических систем.
В-третьих, возможность изменения параметров модели (индуктивностей, сопротивлений) позволяет исследовать различные режимы работы и диагностировать неисправности.
ЗАКЛЮЧЕНИЕ
Представленная математическая модель АДФР на основе метода контурных токов для междуфазных напряжений является эффективным инструментом для исследования переходных процессов, возникающих при различных режимах работы и при наличии несимметрии напряжения питающей сети.
Результаты моделирования подтверждают адекватность разработанной модели и демонстрируют ее применимость для задач релейной защиты и диагностики АДФР.
Список литературы
1. Шестаков А. В., Желнин В. В., Исмиев Р. Н. Экспериментальная проверка математической модели асинхронного двигателя при синусоидальном напряжении // Известия высших учебных заведений. Электромеханика. 2015. № 1. С. 78–85.
2. Шестаков А. В. Математическая модель асинхронного двигателя, учитывающая реальные факторы, при ШИМ-питании // Общество. Наука. Инновации (НПК-2018) : сб. ст. XVIII Всероссийской науч.-практ. конф. в 3 томах, 02–28 апреля 2018 г. г. Киров. Киров : Вятский государственный университет, 2018. Т. 2. С. 1129–1136.
3. Smolyaninov A. V., Pocebneva I. V., Chernenkaya L. V. Mathematical model of asynchronous motor with frequency-cascade regulation // Proceedings of International Russian Automation Conference “RusAutoCon”, September 8–14, 2019, Sochi. Sochi: Institute of Electrical and Electronics Engineers, 2019. p. 8867604. https://doi.org/10.1109/RUSAUTOCON.2019.8867604.
4. Pustovetov M. Y. A mathematical model of the threephase induction motor in three-phase stator reference frame describing electromagnetic and electromechani-cal processes // Proceedings of “Dynamics of Systems, Mechanisms and Machines (Dynamics)”, November 15–17, 2016, Omsk. Omsk: Institute of Electrical and Electronics Engineers Inc., 2017. p. 7819069. https:// doi.org/10.1109/Dynamics.2016.7819069.
5. Глазырин А. С., Полищук В. И., Тимошкин В. В. и др. Математическая модель асинхронного двигателя в мультифазной системе координат при несимметрии роторных цепей // Известия Томского политехнического университета. Инжиниринг георесурсов. 2021. Т. 332, № 10. С. 213–227.
6. Кузнецов В. В., Николенко А. В. О моделях функционирования асинхронного двигателя в условиях некачественной электроэнергии // Восточно-Европейский журнал передовых технологий. 2015. Т. 1, № 8. С. 8.
7. Загребаєв М. С., Звонецький М. С., С’янов О. М. Математичне моделювання перехідних процесів в асинхронному двигуні з короткозамкнутою кліткою в польовій постановці // Математичне моделювання. 2024. № 2. С. 66–76.
8. Яшин А. Н., Гильманов Э. А., Хакимьянов М. И. Моделирование механических характеристик асинхронного двигателя в пакете Matlab Simulink // Электротехнические и информационные комплексы и системы. 2021. Т. 17, № 2. С. 67–75.
Об авторах
Е. Ю. КислицинРоссия
кандидат технических наук, доцент
Д. С. Лукашов
Россия
студент
И. Ю. Борисов
Россия
студент
А. А. Назаров
Россия
студент
Рецензия
Для цитирования:
Кислицин Е.Ю., Лукашов Д.С., Борисов И.Ю., Назаров А.А. Моделирование режимов работы асинхронного двигателя с учетом несимметрии напряжения питающей сети. Вестник кибернетики. 2025;24(1):26-30. https://doi.org/10.35266/1999-7604-2025-1-4
For citation:
Kislitcin E.Yu., Lukashov D.S., Borisov L.Yu., Nazarov A.A. Modeling of induction motor operation modes considering supply voltage asymmetry. Proceedings in Cybernetics. 2025;24(1):26-30. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-4















