Перейти к:
Система сигналов на основе кодов Задова – Чу. Часть 1. Автокорреляционные свойства
https://doi.org/10.35266/1999-7604-2025-3-2
Аннотация
Использование в радиолокации и электрической связи сложных сигналов ограничивается достаточностью исследования их корреляционных свойств, что определяет актуальность исследования и оптимизации сигналов. Показано, что максимальное число вариантов имеет система сигналов, состоящая из простого числа элементов в последовательности. Приведены результаты расчета уровня боковых лепестков автокорреляционной функции такой системы сигналов. Во второй части статьи исследованы взаимнокорреляционные свойства системы сигналов на основе кодов Задова – Чу. Полученные результаты могут быть использованы в электрической связи и радиолокации.
Ключевые слова
Для цитирования:
Дёмко А.И. Система сигналов на основе кодов Задова – Чу. Часть 1. Автокорреляционные свойства. Вестник кибернетики. 2025;24(3):17-25. https://doi.org/10.35266/1999-7604-2025-3-2
For citation:
Dyomko A.I. Signal system based on Zadoff–Chu sequence. Part 1. Autocorrelation properties. Proceedings in Cybernetics. 2025;24(3):17-25. (In Russ.) https://doi.org/10.35266/1999-7604-2025-3-2
ВВЕДЕНИЕ
Многофазная дискретная модуляция имеет множество вариантов реализации, часть из которых обладает примечательными корреляционными свойствами, в частности нулевым уровнем боковых лепестков (УБЛ) периодической автокорреляционной функции (АКФ) [1][4]. Для практических задач во многих случаях более важна импульсная (непериодическая, одиночная) автокорреляционная функция, но сигналы с нулевым УБЛ автокорреляционной функции не известны. Однако некоторые сигналы с нулевым УБЛ периодической АКФ имеют достаточно низкий УБЛ и для импульсной АКФ. В связи с этим актуальными являются исследования непериодических корреляционных свойств систем сигналов, имеющих низкий УБЛ и реализуемые с высокой точностью схемы формирования. Целью статьи является исследование корреляционных свойств системы сигналов на основе кодов Задова – Чу, имеющих нулевой уровень боковых лепестков периодической автокорреляционной функции и низкий уровень боковых лепестков автокорреляционной функции.
МАТЕРИАЛЫ И МЕТОДЫ
Аппроксимация квадратичного закона изменения фазы сигнала с линейной частотной модуляцией [5][7] приводит к сигналам на основе кода Чу [8], которые являются многофазными квадратичными последовательностями (МФКП) – последовательностями, в которых начальная фаза изменяется по квадратичному закону порядкового номера элемента.
Фаза n-го радиоимпульса МФКП определяется выражением (1)
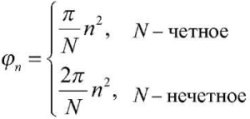 (1)
(1)
n = 0, … N N N – 1,
где N – число элементов в последовательности;
n – порядковый номер элемента, начиная с нулевого.
Сигналы на основе МФКП ортогональны относительно своих циклически сдвинутых версий и имеют нулевой УБЛ периодической АКФ при небольшом уровне боковых лепестков АКФ. В статье рассмотрены корреляционные свойства одиночных (непериодических) МФКП.
На рис. 1 представлена АКФ МФКП из 64 элементов в последовательности.

Рис. 1. Автокорреляционная функция МФКП для N = 64
Примечание: составлено автором на основании данных, полученных в исследовании.
АКФ МФКП имеет ось симметрии при нулевом нормированном сдвиге и дополнительные оси симметрии при сдвигах ±0,5N. Максимальные боковые лепестки АКФ МФКП расположены симметрично на расстоянии ±0,75 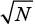 от главного максимума. Уровень боковых лепестков автокорреляционной функции МФКП монотонно уменьшается примерно на 5 дБ/окт при увеличении расстояния от главного максимума вплоть до N/4, далее до N/2 он уменьшается примерно на 3 дБ [9][10].
от главного максимума. Уровень боковых лепестков автокорреляционной функции МФКП монотонно уменьшается примерно на 5 дБ/окт при увеличении расстояния от главного максимума вплоть до N/4, далее до N/2 он уменьшается примерно на 3 дБ [9][10].
На рис. 2 представлена зависимость УБЛ МФКП (в дБ) от числа элементов в последовательности.

Рис. 2. Зависимость УБЛ автокорреляционной функции МФКП от N
Примечание: составлено автором на основании данных, полученных в исследовании.
Уровень максимального бокового лепестка автокорреляционной функции МФКП не зависит от несущей частоты, длительности и периода следования радиоимпульсов, а определяется только числом элементов в последовательности, уменьшаясь (2) на 6 дБ/окт при увеличении N:
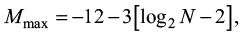 дБ., (2)
дБ., (2)
Несущая частота влияет лишь на тонкую структуру сигнала (положение спектра на оси частот), длительность радиоимпульсов влияет на ширину главного максимума АКФ, период следования определяет наличие и величину нулевых промежутков между боковыми лепестками, распределение и величина которых определяется исключительно начальными фазами радиоимпульсов. Известны многофазные (3) последовательности (коды) Задова – Чу [11]:
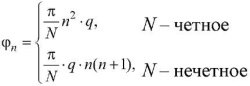 (3)
(3)
n = 0, … N – 1,
где q – целое число, взаимно простое с N.
Примечательность сигналов на основе кодов Задова – Чу состоит в большом объеме различных вариантов [12][13]: для данного числа элементов в последовательности N существует N1 вариантов реализации, определяемых количеством взаимно простых с N чисел q. Следовательно для любого числа элементов в последовательности N существует система из N1 сигналов.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В таблице в качестве примера представлено количество N1 взаимно простых чисел для последовательностей длиной от 5 до 55 элементов.
Таблица
Количество взаимно простых чисел
N | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
N1 | 4 | 2 | 6 | 4 | 6 | 4 | 10 | 4 | 12 | 6 | 8 | 8 | 16 | 6 | 18 | 8 | 12 |
N | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
N1 | 10 | 22 | 8 | 20 | 12 | 18 | 12 | 28 | 8 | 30 | 16 | 20 | 16 | 24 | 12 | 36 | 18 |
N | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 |
N1 | 24 | 16 | 40 | 12 | 42 | 20 | 24 | 22 | 46 | 16 | 42 | 20 | 32 | 24 | 52 | 18 | 40 |
Примечание: составлено автором на основании данных, полученных в исследовании.
Для практического использования системы сигналов на основе кодов Задова – Чу требуется поиск таких последовательностей, для которых, с одной стороны, число вариантов N1 реализации будет максимально большим, с другой стороны, корреляционные свойства максимального их числа будут хорошими (максимальный УБЛ АКФ будет больше требуемого порогового значения).
Максимальное количество взаимно простых чисел N1 получается для последовательностей, состоящих из простого числа элементов (5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, и т. д.):
N1 = N – 1.
Для четного числа элементов число взаимно простых чисел в среднем небольшое (N1 ≈ 0,5N), для нечетного – больше (0,5N ≤ N1 ≤ 0,86N).
Корреляционные свойства сигналов на основе кодов Задова – Чу для разных значений параметра q, который определяет скорость изменения фазы (3), изучены еще в недостаточной степени.
На рис. 3 представлены законы изменения фазы сигналов на основе кодов Задова – Чу из 32 элементов для трех значений параметра q (1, 3, 5), а на рис. 4 – эти же зависимости, приведенные к интервалу 0/360 с учетом периодичности гармонических функций.
Если при разных значениях параметра q качественные отличия исходных законов изменения фазы (3) сигналов на основе кодов Задова – Чу (рис. 3) относительно незначительны, то после преобразования фазы (4) к интервалу 0/360 (рис. 4) эти отличия становятся существенными, причем при увеличении числа элементов N в последовательности отличия нарастают.

Рис. 3. Зависимость фазы сигнала на основе кода Задова – Чу от порядкового номера элемента последовательности n (N = 32)
Примечание: составлено автором на основании данных, полученных в исследовании.

Рис. 4. Зависимость преобразованной фазы сигнала на основе кода Задова – Чу
от порядкового номера элемента последовательности n (N = 32)
Примечание: составлено автором на основании данных, полученных в исследовании.
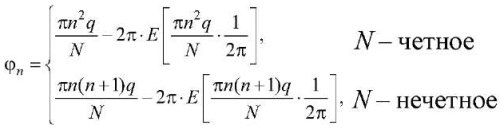 (4)
(4)
где Е [x] – целая часть числа х.
В процессе моделирования установлено, что для различных значений параметра q кода Задова – Чу существенно изменяется структура АКФ, совпадая при двух значениях параметра (q = 1 и q = N – 1) с АКФ кода Чу.
На рис. 5 представлена зависимость УБЛ АКФ сигналов на основе кодов Задова – Чу из 32 элементов от параметра q. Как видно, взаимно простой с N = 32 параметр q принимает в данном случае исключительно нечетные значения.
В среднем УБЛ АКФ для разных значений параметра q имеет значительный разброс, принимая минимальные значения для крайних значений взаимно простых чисел (q = 1 и q = –1). По результатам моделирования установлено, что для любого числа элементов в последовательности имеются значения параметра q, при которых УБЛ достаточно высокий (около –10 дБ).

Рис. 5. Зависимость УБЛ АКФ сигнала на основе кода Задова – Чу из 32 элементов от параметра q
Примечание: составлено автором на основании данных, полученных в исследовании.
На рис. 6 представлена зависимость УБЛ сигналов на основе кодов Задова – Чу в зависимости от параметра q для последовательностей длиной от 5 до 16 элементов.
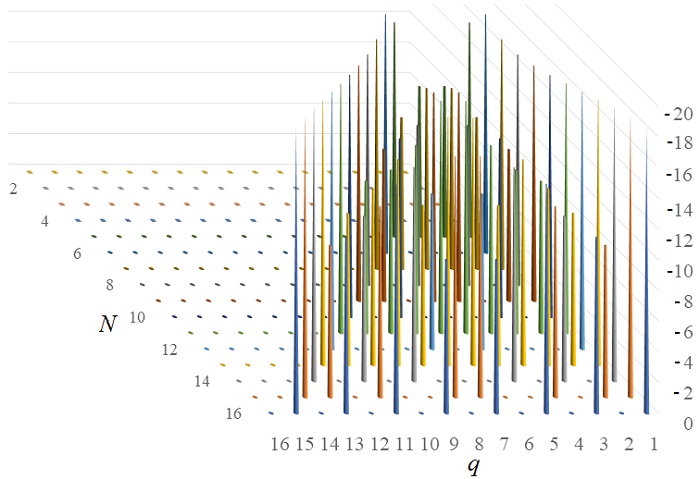
Рис. 6. Зависимость УБЛ АКФ сигнала на основе кода Задова – Чу от параметра q для разного числа элементов в последовательности
Примечание: составлено автором на основании данных, полученных в исследовании.
Анализ приведенных зависимостей демонстрирует нерегулярность структуры (отсутствие некоторых точек означает, что для данного числа элементов последовательности N текущее число q не является с ним взаимно простым). Для крайних значений (q = 1 и q = N – 1) УБЛ принимает значения, аналогичные сигналам на основе кода Чу.
На рис. 7 представлены зависимости числа взаимно простых с N числа элементов (синяя), числа функций с УБЛ АКФ больше –15 дБ (оранжевая), числа функций с УБЛ АКФ больше –18 дБ (серая), числа функций с УБЛ АКФ больше –21 дБ (желтая) в интервале от 210 до 260 элементов последовательности.

Рис. 7. Зависимости числа K взаимно простых с N числа элементов (синяя),
числа функций с УБЛ АКФ больше –15 дБ (оранжевая),
числа функций с УБЛ АКФ больше –18 дБ (серая),
числа функций с УБЛ АКФ больше –21 дБ (желтая)
в интервале от 210 до 260 элементов последовательности
Примечание: составлено автором на основании данных, полученных в исследовании.
Наилучшие результаты (наибольшее число функций с минимальным уровнем боковых лепестков автокорреляционной функции) получаются, когда число элементов в последовательности N является простым числом, средние результаты соответствуют нечетному числу элементов в последовательности и максимальный УБЛ получается при четном числе элементов в последовательности.
На рис. 8 представлены аналогичные рис. 7 зависимости нормированные относительно N в интервале от 7 до 4 093 для простого числа элементов в последовательности.
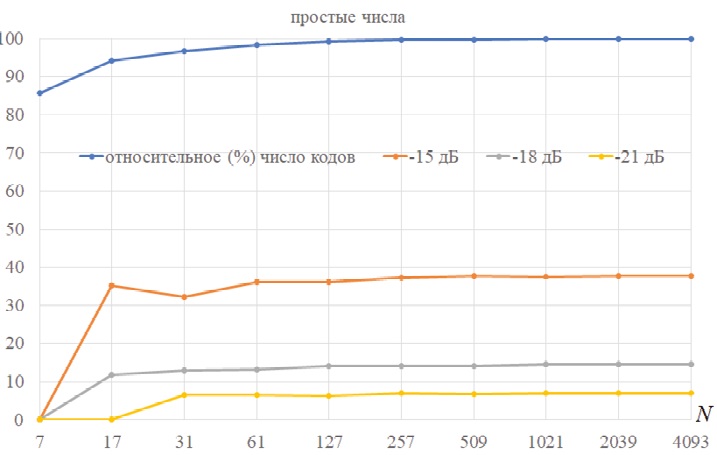
Рис. 8. Зависимости относительного (%) числа взаимно простых с N элементов (синяя),
относительного числа функций с УБЛ АКФ больше –15 дБ (оранжевая),
относительного числа функций с УБЛ АКФ больше –18 дБ (серая),
относительного числа функций с УБЛ АКФ больше –21 дБ (желтая)
в интервале от 7 до 4 093 элементов последовательности
Примечание: составлено автором на основании данных, полученных в исследовании.
При сравнении рис. 8 с рис. 2, который соответствует предельным параметрам кода Задова – Чу, следует, что УБЛ АКФ системы сигналов на основе кода Задова – Чу ранжируется по желаемым пороговым значениям: например, около 0,37N1 сигналов имеют УБЛ АКФ не больше –15 дБ; около 0,14N1 сигналов имеют УБЛ АКФ не больше –18 дБ и лишь около 0,07N1 сигналов имеют УБЛ АКФ не больше –21 дБ, хотя предельные значения УБЛ АКФ для отдельных сигналов из таких систем могут достигать –43 дБ.
Приведенные зависимости УБЛ АКФ и корреляционных свойств дают информацию для выбора параметров сигналов из системы сигналов на основе кодов Задова – Чу в качестве системы сигналов либо для выбора определенных вариантов реализации при ограничении на конкретное число элементов в последовательности N.
ЗАКЛЮЧЕНИЕ
- Сложные системы многофазных радиоимпульсных сигналов на основе кодов Задова – Чу обладают идеальными периодическими автокорреляционными свойствами (нулевой УБЛ периодической АКФ) и реализуемыми схемами формирования.
- Максимальный объем N1 = N – 1 имеют системы сигналов на основе кодов Задова – Чу, состоящие из простого числа элементов N, меньший объем (в интервале от 0,5Nдо 0,86N) для нечетного (не являющегося простым) числа элементов, еще меньше (около 0,5N) – для четного числа элементов.
- Для любого числа элементов Nминимальное значения максимального Mmax бокового лепестка имеют сигналы с двумя значениями взаимно простого с N параметра q (q = 1 и q = N – 1):
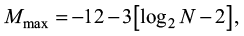 дБ.
дБ.
Для таких сигналов уровень боковых лепестков автокорреляционной функции монотонно уменьшается примерно на 5 дБ/окт при увеличении расстояния от главного максимума вплоть до N/4, далее до N/2 он уменьшается примерно на 3 дБ.
- Уровень максимального бокового лепестка Mmaxавтокорреляционной функции (при q = 1 и q = N – 1) не зависит от несущей частоты, длительности и периода следования радиоимпульсов, а определяется только числом элементов в последовательности, уменьшаясь на 6 дБ/окт при увеличении N.
- Для любого числа элементов N имеются сигналы (при определенных значениях параметра q) с относительно большим уровнем боковых лепестков (–10 дБ).
- При большом числе элементов в последовательности (N > 31) около 0,37N1сигналов системы сигналов имеют максимальное значение уровня боковых лепестков –15 дБ, около 0,14N1 сигналов имеют максимальное значение уровня боковых лепестков –18 дБ и около 0,07N1 сигналов имеют максимальное значение уровня боковых лепестков –21 дБ.
Список литературы
1. Вакман Д. Е. Сложные сигналы и принцип неопределенности в радиолокации. М. : Сов. радио, 1965. 304 c.
2. Вакман Д. Е., Седлецкий Р. М. Вопросы синтеза радиолокационных сигналов. М. : Сов. радио, 1973. 312 с.
3. Фрэнк Р. Л. Многофазные коды с хорошими непериодическими корреляционными свойствами // Зарубежная радиоэлектроника. 1963. T. 17, № 12. С. 39–44.
4. Ипатов В. П. Периодические дискретные сигналы с оптимальными корреляционными свойствами. М. : Радио и связь, 1992. 152 с.
5. Кук Ч., Бернфельд М. Радиолокационные сигналы. Теория и применение / пер. с англ. под ред. В. С. Кельзона. М. : Сов. радио, 1971. 568 с.
6. Комаров И. В., Смольский С. М. Основы теории радиолокационных систем с непрерывным излучением частотно-модулированных колебаний. М. : Горячая линия – Телеком, 2015. 392 с.
7. Варакин Л. Е. Теория систем сигналов. М. : Сов. радио, 1978. 304 с.
8. Chu D. Polyphase codes with good periodic correlation properties // IEEE Transactions on Information Theory. Vol. 18, no. 4. P. 531–532. https://doi.org/10.1109/TIT.1972.1054840.
9. Zhou Z., Helleseth T., Parampalli U. A family of polyphase sequences with asymptotically optimal correlation // IEEE Transactions on Information Theory. 2018. Vol. 64, no. 4. P. 2896–2900. http://dx.doi.org/10.110/TIT.2018.2796597.
10. Дёмко А. И., Семенов О. Ю. Формирование многофазных сигналов с квантованием фазы // Вестник кибернетики. 2022. № 2. С. 39–45. https://doi.org/10.34822/1999-7604-2022-2-39-45.
11. Русанов В. Э. Исследование свойств автокорреляционной функции одного периода последовательности Задова – Чу // Экономика и качество систем связи. 2024. № 1. С. 53–59.
12. Степутин А. Н., Николаев А. Д. Последовательности Задова–Чу (ZC последовательности). URL: https://1234g.ru/book/ZC.pdf (дата обращения: 10.04.2025).
13. Киселева Т. П. Исследование свойств циклической автокорреляционной функции последовательности Задова – Чу в зависимости от характеристик квантования элементов последовательности // Цифровая обработка сигналов. 2018. № 4. С. 40–44.
Об авторе
А. И. ДёмкоРоссия
кандидат технических наук, доцент, почетный работник высшего образования РФ
Рецензия
Для цитирования:
Дёмко А.И. Система сигналов на основе кодов Задова – Чу. Часть 1. Автокорреляционные свойства. Вестник кибернетики. 2025;24(3):17-25. https://doi.org/10.35266/1999-7604-2025-3-2
For citation:
Dyomko A.I. Signal system based on Zadoff–Chu sequence. Part 1. Autocorrelation properties. Proceedings in Cybernetics. 2025;24(3):17-25. (In Russ.) https://doi.org/10.35266/1999-7604-2025-3-2















