Анализ сложности арифметических операций в модулярной системе счисления квадратичного диапазона

ВВЕДЕНИЕ

Модулярная система счисления (МСС) квадратичного диапазона представляет собой расширение традиционной модулярной системы счисления (одинарного диапазона). МСС предназначена для работы в больших числовых областях и специфическими алгоритмами обработки чисел. Она является математической моделью для реализации вычислений на цифровых вычислительных устройствах.

К основным компонентам МСС квадратичного диапазона относятся следующие.

1. Совокупность элементов модулярного квадратичного диапазона.

Элементы этой совокупности представляют собой числа, выраженные в виде вычетов по различным основаниям. Эти основания определяют конкретный диапазон значений, внутри которого проводятся операции над числами. Каждое число записывается в виде остатков от деления на некоторые фиксированные основания – модули.

2. Множество операций.

Операции, выполняемые над представленными в МСС данными, делят на два класса: модульные и немодульные. Модульные характеризуются тем, что при их выполнении не происходит переносов между разрядами. Примерами таких операций являются сложение, вычитание и умножение, деление нацело, умножение на обратный элемент и др. К немодульным операциям отнесены деление, расширение, определение знака, сравнение, определение переполнения, масштабирование, определение ошибки, локализация ошибки, вычисление ранга и др. Для выполнения этих операций, в отличие от модульных, требуется оценка значения числа в целом, которая затруднена в связи с непозиционной природой МСС [1][2].

3. Алгоритмы выполнения операций.

Алгоритмические процедуры предназначены для оптимизации процесса вычислений, минимизации временных затрат и повышения точности результатов.

Вычисления производятся над числами, представленными в типовом машинном формате, который соответствует возможностям конкретного компьютера. Такие числа задаются в виде цифр, соответствующих позициям позиционной системы счисления. Применяется на практике:

– двоичная система, которая используется благодаря простоте аппаратной реализации и эффективности хранения информации;

– шестнадцатеричная система применяется, когда нужна компактность представления больших объемов данных и удобство восприятия человеком.

МАТЕРИАЛЫ И МЕТОДЫ

В данном исследовании основные арифметические операции в МСС реализованы на серийном (позиционном) компьютере.

Серийный компьютер – это вычислительная система классической архитектуры, в которой операнды представлены в позиционной системе счисления (ПСС), а операции выполняются последовательно. Термин «серийный» подчеркивает традиционный подход к обработке данных, в отличие от специализированных систем, таких как модулярные компьютеры.

К основным характеристикам серийных компьютеров можно отнести следующие.

1. Числа представляются в виде последовательности цифр, каждая из которых имеет вес, зависящий от ее позиции (разряда).
2. Последовательная обработка. Операции выполняются последовательно, например, сложение двух чисел выполняется пошагово, начиная с младшего разряда. Сложение, вычитание, умножение и деление выполняются с учетом переносов и заимствований.
3. Традиционная архитектура фон Неймана (один центральный процессор выполняет операции последовательно).

Операции в МСС, реализованные на серийном (позиционном) компьютере, сопровождаются рядом трудностей.

1. Преобразование в ПСС. Числа, представленные в МСС, могут быть преобразованы в ПСС с помощью китайской теоремы об остатках (КТО). После преобразования можно выполнять обычные арифметические операции (сложение, вычитание, умножение и т. д.).
2. Обратное преобразование. После выполнения операций в ПСС результат необходимо снова преобразовать в МСС.

Преобразование между системами счисления требует вычислительных ресурсов.

Введем основные понятия и определения для МСС квадратичного диапазона.

В МСС каждое число представляется в виде набора остатков по соответствующим основаниям (модулям), позволяющим эффективно использовать ресурсы оборудования и минимизировать ошибки округления при выполнении сложных расчетов [3].

Стоит отметить, что в статье модули, по которым вычисляются наименьшие неотрицательные вычеты по модулю (остатки от деления), называются в этой тематике основаниями одинарной или квадратичной МСС.

Определение: Модулярная система счисления квадратичного диапазона – это совокупность математических конструкций и правил, предназначенных для представления и обработки чисел с использованием системы взаимно простых модулей, каждый из которых является квадратом простого числа.

Пусть p₁, p₂, ... p_n – простые числа и пусть m_i = p_i², i = 1, 2, ..., n – соответствующие квадратичные модули. Тогда любое целое число X в диапазоне [0, M − 1], где M = m₁ · m₂ · ... · m_n, может быть однозначно представлено в виде набора остатков:

X = (a₁, a₂, ... a_n) (m₁, m₂, ... m_n),

где a_i – остаток от деления числа X на модуль m_i, то есть a_i = X mod m_i; пара a₁, a₂, ... a_n называется модулярным представлением числа X.

Определение: Квадратичный модуль – это модуль, задаваемый в виде квадрата простого числа ρ, то есть m = ρ².

Определение: Диапазон значений – множество чисел, представленных в МСС с квадратичными модулями, ограничено верхним пределом, равным произведению всех модулей.

Китайская теорема об остатках (КТО) – известная в теории чисел. Из теоремы следует: если заданы попарно взаимно простые модули m₁, m₂, ... m_n, то любое число Y в диапазоне [0, M − 1], где M = m₁ · m₂ · ... · m_n, может быть однозначно представлено своими остатками по этим модулям.

Теорема: Пусть m₁, m₂, ... m_n – попарно взаимно простые числа, то есть НОД(m_i, m_j) = 1 для всех i ≠ j. Тогда система сравнений:

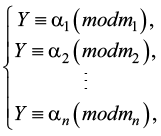
имеет единственное решение Y в диапазоне [0, M − 1], где M = m₁ · m₂ · ... · m_n.

Доказательство.

Пусть модули m₁, m₂, ... m_n попарно взаимно просты, то есть НОД(m_i, m_j) = 1 для всех i ≠ j. Требуется доказать существование и единственность решения Y в указанном диапазоне. 

1. Определим

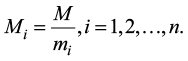
Так как модули попарно взаимно просты, очевидно, что M_i и m_i также взаимно просты для каждого i.

1. Поиск обратных элементов:

Для каждого M_i найдем обратный элемент X_i по модулю m_i, то есть такое число, что:

(X_i ∙ M_i) ≡ 1(mod m_i)

Обратные элементы можно найти с помощью расширенного алгоритма Евклида.

III. Далее воспользуемся формулой:

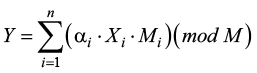
Рассмотрим арифметические операции в МСС квадратичного диапазона.

1. Сложение, вычитание и умножение.

Сложение и вычитание в МСС квадратичного диапазона выполняются поэлементно по каждому модулю с последующим вычислением остатка [1][2][4][5]. Пусть заданы два числа A = α₁ · α₂ · ... · α_n и B = β₁ · β₂ · ... · β_n, где α_i и β_i – остатки по модулям m_i = p_i², а p_i – простые числа. Тогда:

A + B = (α₁ + β₁ (mod m₁), α₂ + β₂ (mod m₂),…, α_n + β_n (mod m_n)),

A – B = (α₁ – β₁ (mod m₁), α₂ – β₂ (mod m₂),…,
α_n – β_n (mod m_n)).

Умножение также выполняется поэлементно с последующим взятием остатка:

A · B = (α₁ · β₁ (mod m₁), α₂ · β₂ (mod m₂),…,
α_n · β_n (mod m_n)).

Результаты операций сложения, вычитания и умножения A + B, A – B и A · B представлены остатками γ_i σ_i и δ_i по тем же основаниям системы счисления m_i.

A + B = (γ₁ , γ₂, ... · γ_n),

A – B = (σ₁ , σ₂, ... · σ_n),

A · B = (δ₁ , δ₂, ... · δ_n),

где γ_i сравнимо с α_i + β_i по модулю m_i, σ_i сравнимо с α_i – β_i по модулю m_i, δ_i сравнимо с α_i · β_i по тому же модулю, выполняются соотношения:

γ_i = α_i + β_i (mod m_i),

σ_i = α_i – β_i (mod m_i),

δ_i = α_i · β_i (mod m_i).

Результатом являются числа:

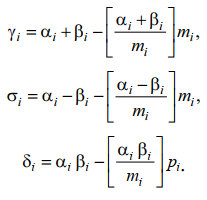
Пример 1. Рассмотрим выполнение данных операций на примере.

В компьютерах, поддерживающих 32-битные числа, типовой диапазон чисел – от 0 до 2³² − 1. Ставится задача – выбрать подходящий набор квадратичных модулей, который покроет этот диапазон, и выполнить операции сложения, вычитания и умножения в МСС.

В качестве оснований выберем взаимно простые числа, квадраты которых дадут достаточное покрытие диапазона: m₁ = 17, тогда p₁ = 172 = 289, m₂ = 19, тогда p₂ = 19 = 361, m₃ = 23, тогда p₃ = 23² = 529, m₄ = 29, тогда p₄ = 29² = 841, m₅ = 31,тогда p₅ = 312 = 961. М = 289 · 361 · 529 · 841 · 961 = 44604646326241 > 2³² − 1 = 4294967295.

Необходимость превышения произведения модулей над машинным диапазоном обусловлена особенностью МCС и требованием полной однозначности представления чисел.

Пусть даны два числа, представленных в МСС: A = (23, 87, 12, 34, 56) и B = (17, 34, 157, 89, 112).

Выполняем поэлементное сложение с последующим взятием остатка по каждому модулю:

A + B = (23 + 17 (mod 289), 87 + 24 (mod 361), 12 + 157 (mod 529), 34 + 89 (mod 841), 56 + 112 (mod 961)) = (40 (mod 289), 121 (mod 361), 169 (mod 529), 1239 (mod 841), 168 (mod 961)) =
= (40, 121, 169, 123, 168).

Аналогично выполняем поэлементное вычитание со взятием остатка:

A−B = (23−17 (mod 289), 87−24 (mod 361), 12−157 (mod 529), 34−89 (mod 841), 56−112 (mod 961)) = (6 (mod 289), 53 (mod 361), 384 (mod 529), 786 (mod 841), 905 (mod 961)) = = (6, 53, 384, 786, 905).

При выполнении операции вычитания в МСС результатом может оказаться отрицательное число. Однако в МСС работают с неотрицательными числами, ограниченными пределами выбранного модуля. Для перевода результата в стандартный вид применяется простая процедура: если число получилось отрицательным, к нему добавляют модуль. Это обусловлено следующими причинами:

1. Периодичность и цикличность.

В МСС действует циклическая арифметика. Если вычитается число и получается отрицательный результат, то это эквивалентно перемещению по кругу на определенное расстояние влево, и возвращение в положительную зону можно выполнить добавлением модуля.

Периодичность и цикличность в МСС позволяют работать с числами в ограниченном диапазоне, создавая эффект возврата в начало при выходе за пределы. Это важнейшее свойство, лежащее в основе модулярной арифметики и обеспечивающее корректность вычислений.

2. Единственное представление.

В МСС каждое число в диапазоне [0, M − 1] должно иметь единственное представление. Появление отрицательного числа нарушает это правило, поэтому нормализация необходима.

3. Последовательность вычислений.

Добавление модуля нормализует результат и восстанавливает нормальное состояние системы, позволяя продолжить вычисления без нарушения законов модулярной арифметики.

На примерах выполним поэлементное умножение с последующим взятием остатка:

A · B = (23 · 17 (mod 289), 87 · 34 (mod 361), 12 · 157 (mod 529), 34 · 89 (mod 841), 56 · 112 (mod 961)) = (391 (mod 289), 2958 (mod 361), 1884 (mod 529), 3026 (mod 841), 6272 (mod 961)) = (102, 70, 297, 503, 506).

2. Возведение в степень.

Возведение в степень в МСС квадратичного диапазона выполняется поэлементно с последующим взятием остатка по каждому модулю.

Пусть A = (23, 87, 12, 34, 56) и k = 5. Необходимо найти A^k.

Для каждого модуля m_i возводим соответствующую компоненту числа A в степень k и берем остаток по модулю m_i.

A⁵ = (235 (mod 289), 875 (mod 361), 125 (mod 529), 345 (mod 841), 565 (mod 961)) =
= (6436343 (mod 289), 4984209207 (mod 361), 248832 (mod 529), 45435424 (mod 841), 550731776 (mod 961)) = (24, 254, 202, 399, 935).

3. Нахождение обратного элемента.

Нахождение обратного числа в МСС квадратичного диапазона выполняется поэлементно с использованием расширенного алгоритма Евклида. Это позволяет эффективно обрабатывать числа и выполнять обратные операции в МСС.

Определение: Обратное число A^–1 по модулю m_i – это такое число, что: A^–1 · A ≡ 1 (mod m_i).

Для каждого модуля m_i находится обратный элемент X_i для соответствующей компоненты числа A по модулю m_i. Будем использовать расширенный алгоритм Евклида для поиска обратных элементов. Рассмотрим его подробно.

Требуется найти обратный элемент Y для числа A по модулю m, то есть такое число Y, что:

A · X ≡ 1 (mod m).

Расширенный алгоритм Евклида основан на классическом алгоритме Евклида для нахождения наибольшего общего делителя (НОД), дополненном поиском коэффициентов Безу.

Алгоритм

1. Начальные условия.

Пусть A и m – заданные числа, причем НОД(A, m) = 1 (условие взаимной простоты). Введем начальные значения: x₀ = 1, x₁ = 0, y₀ = 0, y₁ = 1.

1. Основной цикл.

Пока m ≠ 0, делаем следующие шаги:

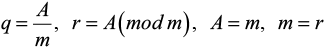
Обновляем коэффициенты:

(x₀, x₁) = ( x₁, x₀ − q · x₁),( y₀, y₁) = ( y₁, y₀ − q · y₁).

III. Завершение цикла.

Когда m = 0, последний ненулевой остаток A – это НОД. Если A = 1, то обратный элемент найден и равен x₀.

Пример 2. Пусть A = (23, 87, 12, 34, 56). Необходимо найти A^–1.

Найдем обратный элемент для A = 23 по модулю m = 289.

1. Начальные условия:

A = 23, m = 289, x₀ = 1, x₁ = 0, y₀ = 0, y₁ = 1.

1. Основной цикл.

Первый шаг:

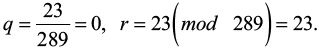
Обновляем коэффициенты:

A = 289, m = 23, x₀ = 0, x₁ = 1, y₀ = 1, y₁ = 0.

Второй шаг:

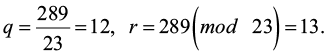
Обновляем коэффициенты:

A = 23, m = 13, x₀ = 1, x₁ = –12, y₀ = 0, y₁ = 1.

Третий шаг:

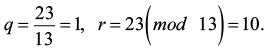
Обновляем коэффициенты:

A = 13, m = 10, x₀ = –12, x₁ = 13, y₀ = 1, y₁ = –1.

Четвертый шаг:

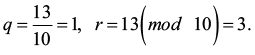
Обновляем коэффициенты:

A = 10, m = 3, x₀ = 13, x₁ = –25, y₀ = −1, y₁ = 2.

Пятый шаг:

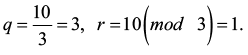
Обновляем коэффициенты:

A = 3, m = 1, x₀ = –25, x₁ = 88, y₀ = −2, y₁ = 7.

Последний шаг:

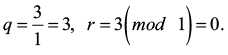
Обновляем коэффициенты:

A = 1, m = 0, x₀ = 88, x₁ = −299, y₀ = −7, y₁ = 23.

III. Завершение.

Последний ненулевой остаток A = 1, следовательно, обратный элемент равен x₀ = 88.

Расширенный алгоритм Евклида позволил найти обратный элемент к числу 23 по модулю 289, он равен 88.

Чтобы проверить результат, подставим его в исходное уравнение:

A · X ≡ 1 (mod m)

23 · 88 ≡ 1 (mod 289)

Вычислим левую сторону: 23 · 88 = 2024.

Теперь возьмем остаток от деления на 289: 2024 (mod 289) = 1.

Таким образом, уравнение выполняется, и 88 действительно является обратным элементом к 23 по модулю 289.

Аналогично, найдем обратные элементы для остальных компонент числа A = (23, 87, 12, 34, 56) по остальным модулям p₂ = 361, p₃ = 529, p₄ = 841, p₅ = 961. Используя расширенный алгоритм Евклида для каждого модуля отдельно, получим:

87 · 83 ≡ 1 (mod 361)

12 · 485 ≡ 1 (mod 529)

34 · 470 ≡ 1 (mod 841)

56 · 532 ≡ 1 (mod 961)

Обратное число для A = (23, 87, 12, 34, 56) по модулям p₁ = 289, p₂ = 361, p₃ = 529, p₄ = 841, p₅ = 961 соответственно: A⁻¹ = (88, 83, 485, 470, 532).

Рассмотрим отдельно случай для компоненты α₅ = 56 числа A, по модулю p₅ = 961. Расширенный алгоритм Евклида позволил нам найти, что обратный элемент к числу 56 по модулю 961 равен –429. Однако в модулярной арифметике результат должен находиться в диапазоне от [0, p₅ − 1]. В нашем случае модуль равен 961.

Чтобы привести результат к нужному диапазону, мы добавляем модуль к отрицательному числу:

–429 + 961 = 532.

Таким образом, –429 эквивалентно 532 по модулю 961.

Нормализация отрицательного результата путем добавления модуля – это стандартная практика в модулярной арифметике, позволяющая приводить результаты к корректному диапазону.

4. Конвертирование в ПСС.

Для перевода числа из МСС в ПСС используется КТО. Она позволяет построить число Y в ПСС, исходя из остатков по каждому модулю.

Пример 3. Пусть задано число в МСС в виде остатков A = (23, 87, 12), модули m₁ = 49, m₂ = 121, m₃ = 169.

1) Находим произведение модулей:

M = 49 ∙ 121 ∙ 169 = 1002001.

2) Вычислим: 

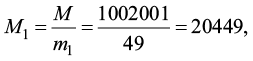
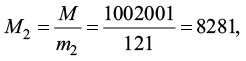
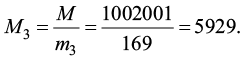
3) Используя расширенный алгоритм Евклида, находим обратные элементы:

Найдем обратный элемент X₁ для M₁ по модулю m₁ = 49:

X₁ = 46, так как 46 ∙ 20449 ≡ 1 (mod 49).

Найдем обратный элемент X₂ для M₂ по модулю m₂ = 121:

X₂ = 16, так как 16 ∙ 8281 ≡ 1 (mod 121).

Найдем обратный элемент X₃ для M₃ по модулю m₃ = 169:

X₃ = 157, так как 157 ∙ 5929 ≡ 1 (mod 169).

4) Собираем результат:

Y = (23 ∙ 46 ∙ 20449 + 87 ∙ 16 ∙ 8281 + + 12 ∙ 157 ∙ 5929) (mod 1002001) = 44332430 (mod 1002001) = 244386.

Таким образом, число A = (23, 87, 12) в позиционной системе равно 244386.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

На языке программирования Python разработаны программы выполнения рассмотренных операций. Приведены фрагменты алгоритмов и результаты (рис. 1–4).

Исходные данные: в МСС квадратичного диапазона представлены числа A = (23, 87, 12, 34, 56) и B = (17, 34, 157, 89, 112). Модулярные основания m₁ = 17, тогда p₁ = 17² = 289, m₂ = 19, тогда p₂ = 19 = 361, m₃ = 23, тогда p₃ = 23² = 529, m₄ = 29, тогда p₄ = 29² = 841, m₅ = 31, тогда p₅ = 31² = 961.

Анализ сложности операций в МСС квадратичного диапазона позволяет оценить ресурсы, необходимые для выполнения операций, и служит важным фактором при выборе подходящей методики и оптимизации производительности [6][8].

Оценка сложности алгоритмов – это мера количества ресурсов времени, необходимого для выполнения алгоритма в зависимости от размера входных данных. Сложность позволяет сравнить алгоритмы и выбрать наиболее эффективный.

Обычно сложность оценивается в следующих терминах. Временная сложность – сколько времени займет выполнение алгоритма и пространственная сложность – сколько памяти потребуется для выполнения алгоритма. Чаще всего рассматривают временную сложность, так как она отражает скорость выполнения.

Проведем анализ сложности операций сложения, вычитания, умножения, возведения в степень и нахождения обратного элемента.

1. Сложение и вычитание. В МСС квадратичного диапазона обе операции выполняются поэлементно по каждому модулю с последующим взятием остатка. Память требуется пропорционально размеру входных данных.

Временная сложность операции сложения: O(n), где n – количество модулей.

В ПСС сложность данных операций напрямую зависит от размера чисел, участвующих в расчетах. Операции занимают время порядка O(n), где n – количество цифр в числе (базисная единица измерения сложности).

2. Умножение. В МСС квадратичного диапазона операция умножения также выполняется поэлементно с последующим взятием остатка.

Временная сложность операции сложения: O(n), где n – количество модулей.

Для сравнения в позиционной системе счисления (ПСС) сложность следующая:

– классический метод: сложность O(n ²), где n – количество цифр в числе.

– быстрый метод (Карацуба): сложность O(n^log23).

– самый быстрый известный метод (FFT): сложность O(n log n) где n – размер входных данных.

В ПСС при умножении двух чисел длиной n цифр нужно выполнить n ² операций сложения и переноса, что и приводит к квадратичной сложности.

В МСС квадратичного диапазона же каждое умножение выполняется отдельно по каждому модулю, что существенно снижается до линейной сложности.

3. Возведение в степень. Используется быстрый алгоритм Binary Exponentiation, который снижает сложность возведения в степень до O(log k), где k– показатель степени. Однако, поскольку эта операция выполняется для каждого модуля, общая временная сложность составит O(n ∙ log k).

В ПСС операция возведения числа в степень имеет следующую сложность.

Простой метод: сложность O(n^k), где n – количество цифр, k – показатель степени.

Быстрый метод (Binary Exponentiation): сложность O(n ∙ log k).

В ПСС возведение в степень приводит к росту числа разрядов, что требует больших ресурсов для обработки.

4. Нахождение обратного элемента. Используется расширенный алгоритм Евклида, который требует O(n∙ log M) операций, где M – максимальный модуль. Учитывая, что мы выполняем эту операцию для каждого модуля, общая временная сложность составит O(n ∙ log M).

Таблица показывает временную сложность арифметических операций для одинарной и квадратичной, а также позиционной систем счисления. Все они используются для отображения чисел из одинаковых числовых диапазонов. Обозначения в МСС: n – количество модулей, k – показатель степени, M – максимальный модуль; в ПСС: n – размер входных данных (количество цифр в числе), k – показатель степени. 

Из таблицы можно заметить, что сложность арифметических операций для одинарной и квадратичной МСС одинаковая. Причина заключается в том, что фундаментальная структура операций в обеих системах идентична и ключевым параметром является не сама величина модулей, а их количество. Количество шагов остается постоянным, и разница проявляется лишь в максимальном диапазоне представлений чисел, но не в самой процедуре вычислений.

ЗАКЛЮЧЕНИЕ

Исследование посвящено анализу модулярной системы счисления квадратичного диапазона, ее структуре и особенностям выполнения основных арифметических операций на серийных (позиционных) компьютерах. Оцениваются временные затраты на выполнение основных арифметических операций в сравнении с позиционными системами счисления. На языке программирования Python разработан алгоритм выполнения основных арифметических операций, приведены результаты его работы.

Проведенное исследование позволяет сделать следующие выводы:

1. Рассмотренные в исследовании арифметические операции характеризуются низкой сложностью и высокой эффективностью. Большинство операций линейны относительно количества модулей, что обеспечивает быструю обработку данных. Как видно из таблицы, это операции сложения, вычитания и умножения. Линейные операции O(n) масштабируются линейно с ростом количества модулей, что делает их очень эффективными и быстрыми даже при большом количестве модулей. К логарифмическим операциям относятся возведение в степень и нахождение обратного элемента. Операция возведения в степень O(n∙ log k) эффективна при умеренных показателях степени, но при очень больших степенях может замедляться. Нахождение обратного элемента O(n ∙ log M) также может замедляться при росте максимального модуля, но в целом остается достаточно эффективной для большинства практических задач.

Большинство операций в МСС квадратичного диапазона имеют низкую сложность и обеспечивают высокую производительность. Линейные операции особенно привлекательны для крупномасштабных вычислений, тогда как операции с логарифмической зависимостью требуют внимания к размерам показателей степени и модулей.

2. Моделирование МСС квадратичного диапазона на серийных компьютерах имеет свои преимущества и недостатки. К преимуществам можно отнести универсальность и простоту реализации. Серийные компьютеры могут выполнять широкий спектр задач, используя стандартные алгоритмы и архитектуры.

К недостаткам реализации МСС квадратичного диапазона на серийном компьютере можно отнести следующие:

– медленная обработка – преобразование между системами счисления требует значительных вычислительных ресурсов. Операции в ПСС выполняются последовательно, что снижает производительность;

– большой объем данных – представление чисел в МСС может потребовать больших объемов памяти для хранения промежуточных результатов;

– ограниченные возможности параллельной обработки – серийные компьютеры не приспособлены для параллельной обработки данных, что делает их менее эффективными для массовых вычислений.

Серийные компьютеры широко используются в жизни и науке. Они универсальны, что делает их популярными в различных областях, от персональных компьютеров до серверов и суперкомпьютеров.

Альтернативой серийным компьютерам являются специализированные многопроцессорные (модулярные) компьютеры.

Специализированные многопроцессорные компьютеры, работающие с МСС, специально разработаны для параллельной обработки данных. Они позволяют эффективно выполнять операции в МСС, распределяя нагрузку между процессорами и используя преимущества параллельных вычислений. Целесообразно рассмотреть сложность выполнения операций в специализированных многопроцессорных компьютерах, которые разработаны для работы с МСС и обеспечивают высокую производительность.