Перейти к:
Представление сетей Петри в матрично-предикатном виде
https://doi.org/10.35266/1999-7604-2025-3-8
Аннотация
Разработанный авторами матрично-предикатный метод задания конечных графов, примененный для задания конечных автоматов, можно применить и для задания сетей Петри, которые являются двудольным (направленным) мультиграфом. Сеть Петри также можно представить квадратной матрицей в матрично-предикатном виде. Это позволит применять аппарат теории матриц при проведении математических (теоретико-множественных и логических) операций над сетями Петри. Применение в задании сетей элементов теории предикатов позволит повысить гибкость в управлении ими.
Для цитирования:
Поляков В.С., Авдеюк О.А., Никулин Р.Н. Представление сетей Петри в матрично-предикатном виде. Вестник кибернетики. 2025;24(3):72-78. https://doi.org/10.35266/1999-7604-2025-3-8
For citation:
Polyakov V.S., Avdeyuk O.A., Nikulin R.N. Representation of Petri nets in matrix-predicate form. Proceedings in Cybernetics. 2025;24(3):72-78. (In Russ.) https://doi.org/10.35266/1999-7604-2025-3-8
ВВЕДЕНИЕ
Сложные системы представляют собой совокупность последовательно и параллельно функционирующих блоков, узлов, компонентов и прочих составляющих. При их построении чаще всего используются следующие методы:
– конечных автоматов,
– сетей Петри,
– нейронных сетей.
При реализации каждого из этих методов используется свой математический аппарат, имеющий свои достоинства и свои недостатки.
Для изучения и работы с моделируемыми системами важным инструментом благодаря своей способности описывать различные классы параллельных, дискретных, асинхронных, распределенных и недетерминированных систем является сеть Петри. Она обеспечивает наглядное описание их функционирования и обладает качественным программным и математическим аппаратом для анализа [1][2].
В отличие от конечных автоматов, сеть Петри – это композиция графа и дискретной системы, позволяющая реализовать математическую модель параллельной системы и моделировать широкий класс сложных систем. Как правило, для этой цели используются достаточно простые, общего вида сети. Однако для некоторых подклассов сложных систем используются расширения сетей Петри: временные, иерархические, ингибиторные, раскрашенные сети и другие, подобные им. Но для каждого из этих расширений необходима корректировка используемого математического аппарата, поскольку сетям Петри присущи некоторые недостатки [3][4].
МАТЕРИАЛЫ И МЕТОДЫ
Теория сетей Петри развивается в двух основных направлениях:
– формальная теория сосредоточена на определении и создании понятий, методов и способов работы с сетями;
– прикладная теория включает разработку методов анализа и моделирования с использованием сетей Петри [5].
Классический способ определения сети Петри (PN). Традиционно сети Петри можно задать в аналитическом, графическом или матричном виде.
Аналитический способ задания сетей Петри. Сеть Петри состоит из двух компонентов:
– собственно сети, которая определяется структурой сети;
– маркировкой позиций (мест) сети, с помощью которой определяется функционирование сети [6][7].
Структура сети представляет собой 4-кортеж (P, T, I, O) и является двудольным (направленным) мультиграфом, дуги которого соединяют узлы двух непересекающихся множеств:
множества позиций P, представляющих собой состояния
P = {p1, p2, ..., pi, pn},
множества переходов T, показывают действия
T = {t1, t2, ..., ti, tn}.
Переходы и позиции, соединенные дугами fk, делятся на два типа: направленные от позиции к переходам (p – t), а также от переходов к позициям (t – p). Таким образом, формально сеть Петри представляется как совокупность множеств:
N = (P, T, F),
здесь P – множество позиций,
T – множество переходов,
F – множество дуг сети, причем F(p – t) ⋃ F(t – p),
где F(p – t) – множество дуг, ведущих от позиций к переходам,
F(t – p) – множество дуг, ведущих от переходов к позициям.
При таком представлении функционирование сети представляется как взаимодействие позиций и переходов в ней.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Рассмотрим для переходов tj следующие функции:
– ввода I(tj): T → P (отображение из множества переходов в комплекты позиций);
– выхода O(tj): T → P (отображение из множества переходов в комплекты позиций). Таким образом, в этом случае для перехода tj → T определяются входные I(tj) и выходные O(tj) позиции сети, то есть позиция pi будет входной позицией перехода tj, если pi ∈ I(tj) и будет выходной позицией этого перехода, если pi ∈ O(tj).
Определим для позиций pi следующие функции:
– ввода I(pi): P → T (отображение из множества позиций в комплекты переходов);
– выхода O(pi): P → T (отображение из множества позиций в комплекты переходов). Таким образом, в этом случае для позиции ti ∈ P определяются входные I(pi) и выходные O(pi) переходы сети, то есть переход tj будет входным переходом позиции pi, если ti ∈ I(pi) и будет выходным переходом этой позиции, если ti ∈ O(pi).
Сети Петри представляют собой двудольный (направленный) мультиграф, что означает, что входы и выходы элементов сети могут быть представлены несколькими дугами. Таким образом, они описываются не множествами, а комплектами [8].
В таком случае сеть Петри можно представить 4-кортежем (P, T, I, O).
Пример:
Задана структура сети Петри C = (P, T, I, O, M), где
P = {p1, p2, p3, p4, p5} – множество мест (позиций) сети,
T = {t1, t2, t3, t4} – множество переходов сети,
I – функция входа: I(t1) = {p1},
I(t2) = {p1, p3, p5},
I(t3) = {p3},
I(t4) = {p4},
O – функция выхода: O(t1) = {p2, p3, p5},
O(t2) = {p5},
O(t3) = {p4},
O(t4) = {p2, p3}.
Приведенная выше структура сети Петри состоит из пяти позиций, четырех переходов и тринадцати дуг.
Графический способа задания сетей Петри. Таким образом, сеть Петри можно представить как двудольный мультиграф, дуги которого соединяют вершины двух непересекающихся множеств (P и T). Вершины P множества P изображают кружками, а вершины tj ∈ T – полочками. Дуги этого мультиграфа всегда направлены либо из вершин множества P к вершинам множества T, либо наоборот – из вершин множества T к вершинам множества P.
Рассмотренная ранее в примере 1 структура сети Петри представлена на рисунке (рис. 1).
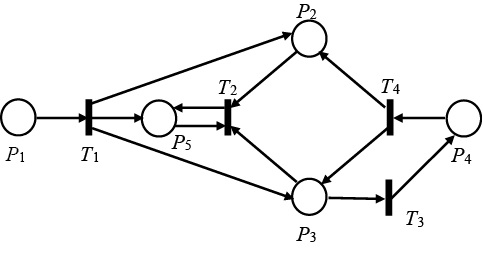
Рис. 1. Структура сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Задание сетей Петри матричным способом. Для задания инцидентности вершин сети Петри эффективно применение матриц. Иными словами, сеть Петри задают двумя матрицами Q и R, имеющими n столбцов (по числу вершин позиций pε) и k строк (по числу вершин переходов tj) (рис. 2).
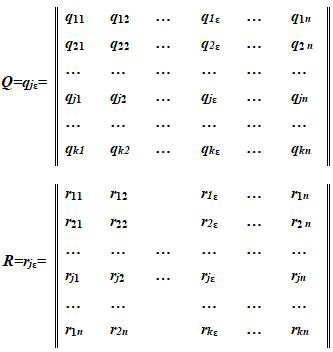
Рис. 2. Матричный способ сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Элементами матриц являются нули и единицы, которые отражают значения элементов qjε и rjε, заданные выражениями.
Элемент qjε равен единице, если есть дуга от вершины позиции pε к вершине перехода tj, и равен нулю в случае отсутствия дуги.
Элемент rjε равен единице, если имеется дуга от вершины перехода tj к вершине позиции pε, и равен нулю в случае отсутствия дуги.
При задании сети Петри любым из указанных выше способов всегда возможно перейти к любому другому эквивалентному виду задания. Для наглядности часто используются графические методы, в то время как при работе с сетями Петри на компьютере чаще всего применяются аналитические и матричные подходы, что позволяет оперировать с векторами и матрицами.
Маркировка и функционирование сетей Петри. Функционирование сети Петри, с одной стороны, определяется маркировкой сети: присвоением фишек позициям, количеством и расположением их, а с другой стороны – разработанной методикой изменения маркировки позиций и правилами срабатывания переходов.
Функционирование сети Петри можно определить как процесс присвоения фишек позициям, количество и расположение которых будут меняться. Маркировка сети Петри определяется как отображение множества позиций P в множество неотрицательных целых чисел.
μ : P → N,
где i – метки, P – позиции, N – целые числа.
Маркировка сети Петри может быть определена как вектор M:
M = (μ1, μ2, ..., μi, ..., μn),
где n = |P|, каждое μi ∈ N, i = 1, ..., n.
Маркированная сеть Петри представляет собой 5-кортеж (P, T, I, O, M).
Зададим начальную маркировку сети Петри, структура которой рассмотрена в примере 1 на рисунке (рис. 1). Маркировка M0 = (1,1,0,0,1) означает, что фишки поставлены в позициях 1, 2 и 5. Маркированная сеть Петри примет вид, показанный на рис. 3.
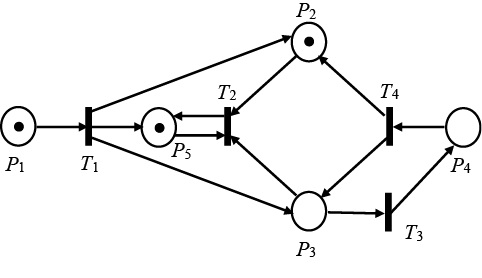
Рис. 3. Маркированная сеть Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Работа сети осуществляется через активацию переходов. Предположим, что переход tj имеет mj входящих позиций и каждая из этих позиций содержит количество фишек, которое равно или превышает число дуг, которые соединяют позицию с переходом. Под активацией перехода подразумевают удаление всех разрешающих фишек из его входных позиций и добавление в каждую из выходных позиций фишек в количестве, которое равно числу дуг, ведущих от перехода.
Этот процесс будет осуществляться до тех пор, пока не останется ни одного разрешенного перехода, после чего функционирование сети прекращается.
Рассмотрим сеть Петри, заданную графически (рис. 4), начальная маркировка которой M0 = (1,1,0,0,1). Данная маркировка открывает только один переход – T1.
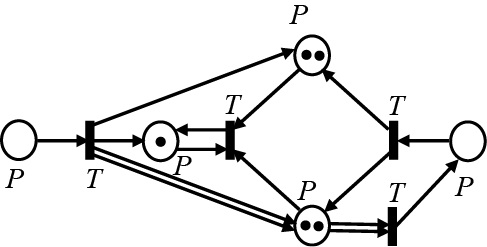
Рис. 4. Маркированная сеть Петри. Открыт переход T7
Примечание: составлено авторами на основании данных, полученных в исследовании.
Результатом запуска перехода T1 будет сеть с маркировкой (рис. 5).
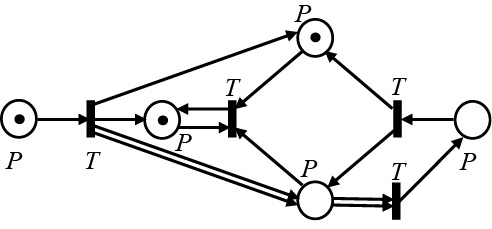
Рис. 5. Маркированная сеть Петри. Результат срабатывания перехода T1
Примечание: составлено авторами на основании данных, полученных в исследовании.
Структура матрично-предикатного представления сетей Петри. Сеть Петри можно представить в виде блок-схемы (рис. 6).

Рис. 6. Блок-схема сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Сеть Петри является двудольным (направленным) мультиграфом G(A, E) ,
где A = P ⋃ T – множество вершин,
E – инцидентор, задающий взаимосвязь вершин. Под этим понимаем связь между элементами, когда вершина инцидентна ребру.
Любой граф может быть представлен в матрично-предикатном виде. Представим матрицу этого графа G(A, E) в виде квадратной матрицы, состоящей из четырех частей (рис. 7).
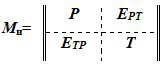
Рис. 7. Матрица графа
Примечание: составлено авторами на основании данных, полученных в исследовании.
На рис. 7 приняты следующие обозначения:
P = ‖pi‖ – подматрица вершин-позиций;
T = ‖ti‖ – подматрица вершин-переходов;
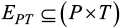 – подматрица, представляющая часть инцидентора, описывающего переход из состояния позиций сети Петри в состояние переходов;
– подматрица, представляющая часть инцидентора, описывающего переход из состояния позиций сети Петри в состояние переходов;
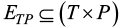 – подматрица, представляющая часть инцидентора, описывающего переход из состояния переходов сети Петри в состояние позиций.
– подматрица, представляющая часть инцидентора, описывающего переход из состояния переходов сети Петри в состояние позиций.
Часть P матрицы MИ (рис. 8) – это диагональная матрица, представляющая собой несвязный граф, который задает множество позиций сети Петри.

Рис. 8. Диагональная матрица P, описывающая множество позиций сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
С помощью этой части матрицы MИ осуществляется маркировка сети Петри, которая осуществляется присвоением фишек i позициям (рис. 9).
Маркированная сеть Петри представляет собой 5-кортеж (P, T, I, O, M).

Рис. 9. Маркированная матрица P, описывающая позиции сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Часть T матрицы MИ (рис. 10) – это диагональная матрица, представляющая собой несвязный граф, который задает множество переходов сети Петри.

Рис. 10. Диагональная матрица P, описывающая множество переходов сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Часть EPT матрицы MИ (рис. 11) – это часть инцидентора, представляющая истинные значения предиката (диагональные элементы матрицы MИ определяются трехместным предикатом PiμiPi или TjμjTj, а для задания недиагональных ненулевых элементов матрицы MИ трехместный предикат доопределяется двумя местами, определяющими кратности дуг этих входов и выходов), который связывает конкретные позиции сети (матрица P) с соответствующими переходами сети (матрица T).
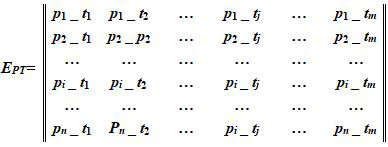
Рис. 11. Матрица EPT, описывающая взаимодействие позиций и переходов сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Часть ETP матрицы MИ (рис. 12) – это часть инцидентора, представляющая истинные значения предиката, который связывает конкретные переходы сети (матрица T) с соответствующими позициями сети (матрица P).

Рис. 12. Матрица ETP, описывающая взаимодействие переходов и позиций сети Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
Подставим в матрицу MИ значения частей P, T, EPT, ETP и получим обобщенную матрицу, приведенную на рисунке (рис. 13).

Рис. 13. Матрица MИ, описывающая сеть Петри
Примечание: составлено авторами на основании данных, полученных в исследовании.
В качестве примера использования эффективности нового представления сетей Петри можно привести сложные многокомпонентные системы с десятками компонентов, функционирующих параллельно-последовательным образом. Это могут быть интеллектуальные системы управления движениями судов по системе каналов, выявления аварийных и предаварийных состояний на производственных линиях и в иных областях.
ЗАКЛЮЧЕНИЕ
Таким образом, предложенная в работе методика представления сетей Петри позволяет существенно упростить работу с ними и использовать этот аппарат при построении сложных систем различного рода, представляющих собой совокупность последовательно и параллельно функционирующих компонентов, а также более эффективно работать с параллельными, асинхронными и недетерминированными процессами в проектируемых сложных системах.
Список литературы
1. Лескин А. А., Мальцев П. А., Спиридонов А. М. Сети Петри в моделировании и управлении. Л. : Наука, 1989. 133 с.
2. Bechhofer S., Goble C. Thesaurus construction through knowledge representation // Data & Knowledge Engineering. 2001. Vol. 37, no. 1. P. 25–45. https://doi.org/10.1016/S0169-023X(00)00052-5.
3. Лоу А. М., Кельтон В. Д. Имитационное моделирование. 3-е изд. / пер. с англ. СПб. : Питер, 2004. 847 с.
4. Тулохонова И. С., Отбоева С. Д. Решение частной задачи проектирования на основе сети Петри // Интернет-журнал Науковедение. 2016. Том 8. № 4.
5. Маслаков М. П., Маслаков Д. П. Операции над сетями Петри // Физико-математические науки и информационные технологии: актуальные проблемы : материалы Междунар. заоч. науч.-практ. конф., 11 июня 2012 г., г. Новосибирск. Новосибирск : СибАК, 2012. С. 12–17.
6. Badouel E., Bernardinello L., Darondeau P. Petri net synthesis. Springer, 2015. 339 p.
7. Best E., Devillers R. Characterisation of the state spaces of marked graph Petri nets // Information and Computation. 2017. Vol. 253. Pt. 3. P. 399–410. https://doi.org/10.1016/j.ic.2016.06.006.
8. Schlachter U. Petri net synthesis for restricted classes of nets // Proceedings of the 37th International Conference “Petri Nets 2016”, June 19–24, 2016, Toruń. Toruń: Springer-Verlag, 2016. P. 79–97.
Об авторах
В. С. ПоляковРоссия
кандидат технических наук, доцент
О. А. Авдеюк
Россия
кандидат технических наук, доцент
Р. Н. Никулин
Россия
кандидат физико-математических наук, доцент
Рецензия
Для цитирования:
Поляков В.С., Авдеюк О.А., Никулин Р.Н. Представление сетей Петри в матрично-предикатном виде. Вестник кибернетики. 2025;24(3):72-78. https://doi.org/10.35266/1999-7604-2025-3-8
For citation:
Polyakov V.S., Avdeyuk O.A., Nikulin R.N. Representation of Petri nets in matrix-predicate form. Proceedings in Cybernetics. 2025;24(3):72-78. (In Russ.) https://doi.org/10.35266/1999-7604-2025-3-8















