Перейти к:
РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ КИНЕМАТИКИ ДЛЯ ШЕСТИЗВЕННОГО РОБОТА-МАНИПУЛЯТОРА
https://doi.org/10.35266/1999-7604-2024-2-5
Аннотация
В работе описана последовательность действий, необходимых для решения прямой задачи кинематики, ориентированной на шестизвенного робота-манипулятора FANUC Robot M-20iA/35M. Решение задачи базируется на использовании современных технологий твердотельного CAD-моделирования совместно со средой физического моделирования, многозвенных пространственных механизмов SimMechanics системы Simulink. Среда SimMechanics системы Simulink используется для визуализации динамики движения рабочего органа манипулятора. Полученное выражение матрицы манипулятора позволит в дальнейшем использовать его для решения обратной задачи кинематики.
Ключевые слова
Для цитирования:
Гусев О.В. РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ КИНЕМАТИКИ ДЛЯ ШЕСТИЗВЕННОГО РОБОТА-МАНИПУЛЯТОРА. Вестник кибернетики. 2024;23(2):39-48. https://doi.org/10.35266/1999-7604-2024-2-5
For citation:
Gusev O.V. SOLVING THE DIRECT KINEMATIC PROBLEM FOR A SIX-UNIT ROBOT MANIPULATOR. Proceedings in Cybernetics. 2024;23(2):39-48. (In Russ.) https://doi.org/10.35266/1999-7604-2024-2-5
ВВЕДЕНИЕ
Манипуляционные роботы являются основными компонентами современных робототехнических комплексов и, как правило, имеют множество степеней свободы или подвижности. Последнее дает возможность перемещать их исполнительные органы в трехмерном пространстве и выполнять комплексные задачи. Для моделирования перемещения исполнительного механизма робота необходимо решить задачи кинематики и динамики.
Кинематика манипуляторов описывает движение робототехнической системы в трехмерном евклидовом пространстве относительно заданной абсолютной системы координат в зависимости от времени, но без учета сил и моментов, которые порождают такое движение. Иными словами, задача кинематики – это описание пространственного положения манипулятора как функции времени. Кинематическая задача разделяется на прямую и обратную. Прямая задача кинематики служит для определения пространственных координат рабочего инструмента манипулятора по значениям координат и углов его шарнирных соединений.
Обратная позиционная кинематическая задача заключается в определении значений обобщенных координат шарниров манипулятора по заданному положению исполнительного органа.
При динамическом анализе работы необходимо по известным значениям сил и моментов, развиваемых приводами манипулятора, определить параметры движения его звеньев, обратная задача – в том, чтобы по заданным обобщенным координатам, скоростям и ускорениям определить действующие в сочленениях манипулятора силы и моменты. Аналитический подход, используемый для решения задачи кинематики и динамики, является сложным и затратным с точки зрения вычислительных ресурсов.
В статье предложено решение прямой задачи кинематики для промышленного робота-манипулятора FANUC Robot M-20iA/35M [1].
МАТЕРИАЛЫ И МЕТОДЫ
FANUC Robot M-20iA/35M представляет собой стационарный шестиосевой робот с подвижной рукой. В качестве исполнительных двигателей применяются электрический сервопривод, шестиступенчатые шарнирные соединения с возможностью переворачиваться назад для увеличения рабочего диапазона и обеспечения максимальной гибкости. На рис. 1 показана конструкция робота и наименование и обозначение осей устройства (рис. 1a) с направлением вращения и пределам вращения по углам. На рис. 1б показано рабочее пространство манипулятора в виде диаграммы движения.
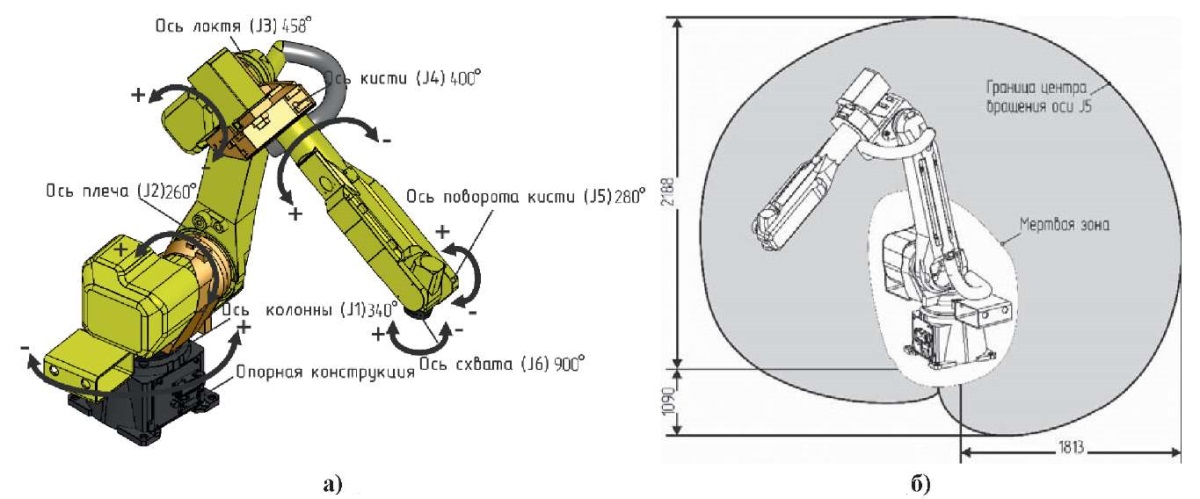
Рис. 1. Конструкция робота FANUC Robot M-20iA/35M
а) составные части и оси манипулятора;
б) диаграмма движения манипулятора по осям
Примечание: составлено автором.
Robot M-20iA/35M является манипулятором с шестью степенями свободы, составные части манипулятора перемещаются в пространстве с помощью шести серводвигателей, которые размещаются в осях вращения (суставах) робота. Каждый роботизированный сустав перемещается в определенном диапазоне углов. На рис. 1а сочленения (joint) звеньев манипулятора обозначены буквами J1...J6. Кинематическая цепь манипулятора состоит из шести кинематических пар вращательного типа, Robot M-20iA/35M работает в ангулярной (антропоморфной) системе координат, представляющей собой сферу (рис. 1б). Основные механические характеристики, а также пределы вращения по осям даны в таблице.
Таблица
Механические характеристики FANUC Robot M-20iA/35M
Характеристики | Значение | |
Способ монтажа | Напольный/настенный/наклонная поверхность | |
Количество осей подвижности | 6 (J1, J2, J3, J4, J5, J6) | |
Радиус рабочей зоны, мм | 1 813 | |
Движение по осям, °/ Скорость движения по осям, °/с | - (J1) ось колонны | 340°/370° (опционно) (180°/с) |
- (J2) ось плеча | 260° (180°/с) | |
- (J3) ось локтя | 458° (200°/с) | |
- (J4) ось вращения запястья | 400° (350°/с) | |
- (J5) ось поворота запястья | 280° (350°/с) | |
- (J6) ось вращения фланца | 900° (400°/с) | |
Допустимый момент инерции по осям, Н∙м | J4 | 110,0 |
J5 | 110,0 | |
J6 | 60,0 | |
Допустимый крутящий момент по осям, кг∙м² | J4 | 4,00 |
J5 | 4,00 | |
J6 | 1,50 | |
Максимальная грузоподъемность, кг | 35 | |
Вес тела манипулятора (без блока управления), кг | 252 | |
Точность повторного позиционирования, мм | ±0,08 | |
Примечание: составлено на основании источника [1].
Конструкция роботизированного манипулятора FANUC Robot M-20iA/35M стандартна для своего типа и состоит из неподвижного основания, с которым связана базовая система координат, поворотной стойки, к которой крепятся составные узлы манипулятора и его рабочий орган (концевой эффектор). При такой конструкции концевой эффектор манипулятора имеет возможность занять любое положение в его рабочем пространстве. В твердотельной модели рабочий орган не показан и используется его имитация в виде сферы. В реальном проекте в качестве концевого эффектора предполагается использовать систему технического зрения (СТЗ) для визуализации и обработки объекта сложной формы [2].
Для реализации поставленной цели необходимо рассчитать прямую и обратную кинематическую задачу. Прямая задача связана с определением пространственных координат рабочего органа манипулятора FANUC Robot M-20iA/35M по значением углов поворота его звеньев (шарниров). Обратная задача кинематики – расчет набора обобщенных координат звеньев манипулятора по заданной позиции рабочего органа манипулятора. К изучению кинематики, т. е. к описанию движения манипулятора, можно подойти, рассмотрев две дополняющие друг друга задачи (см. рис. 2).
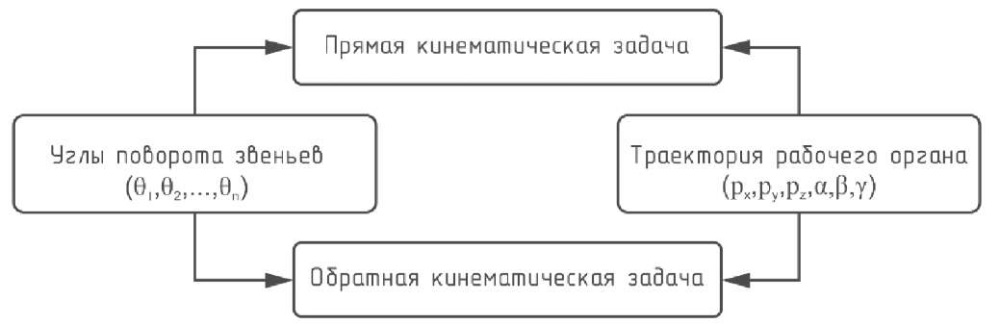
Рис. 2. Блок-схема процесса кинематического анализа
Примечание: составлено автором.
При решении поставленных задач предполагается, что СТЗ фиксируется на рабочем инструменте робота-манипулятора и позволяет осуществить распознавание искомого объекта, а также определить его месторасположение в пространстве. Дальнейшая обработка полученного с помощью СТЗ изображения позволит обнаружить дефекты анализируемой поверхности (повреждения, разрывы и т. д.). Таким образом, необходимо решить обратную кинематическую задачу – вычисления углов сочленений манипулятора, так, чтобы концевой эффектор занимал определенное положение и ориентацию относительно анализируемой поверхности. В качестве модели сложной поверхности в дальнейшем будет использована модель рабочей лопатки 4-й ступени ротора компрессора низкого давления.
Обратная кинематическая задача может быть решена в численном либо аналитическом виде [3][4]. Аналитический метод решения обратной задачи для многозвенного манипулятора основан на использовании аппарата тригонометрических функций. Преимуществом аналитического метода является получение решения с произвольной точностью, однако получение аналитического решения не всегда возможно для произвольной конструкции манипулятора. Использование численных методов позволяет решить обратную задачу кинематики для тех конструкций манипуляторов, для которых получение точного решения в аналитических выражениях не представляется возможным либо достаточно затруднительно [5].
На рис. 3 схематически показана кинематическая схема манипулятора, а также оси вращения его сочленений. Шесть степеней свободы манипулятора Robot M-20iA/35M обеспечивают эффективное и точное позиционирование его конечного эффектора. Число степеней свободы связано с числом одноосных вращательных соединений в звеньях манипулятора (ось вращения шестого звена манипулятора, которая отвечает за вращение шпинделя конечного эффектора, не бралась в расчет, т. е. полагалось, что конечный эффектор манипулятора неподвижен) [6]. Звенья манипулятора связаны вращательными кинематическими парами пятого класса (кинематическая схема разомкнута). Направление осей вращения задается в соответствии с правилом правой руки: пальцы правой руки согнуты в направлении вращения, большой палец правой руки направлен в положительном направлении оси. Сочленения (joint) звеньев манипулятора обозначены буквами J1…J5, точка крепления рабочего органа (end-effector) обозначена буквами EE.
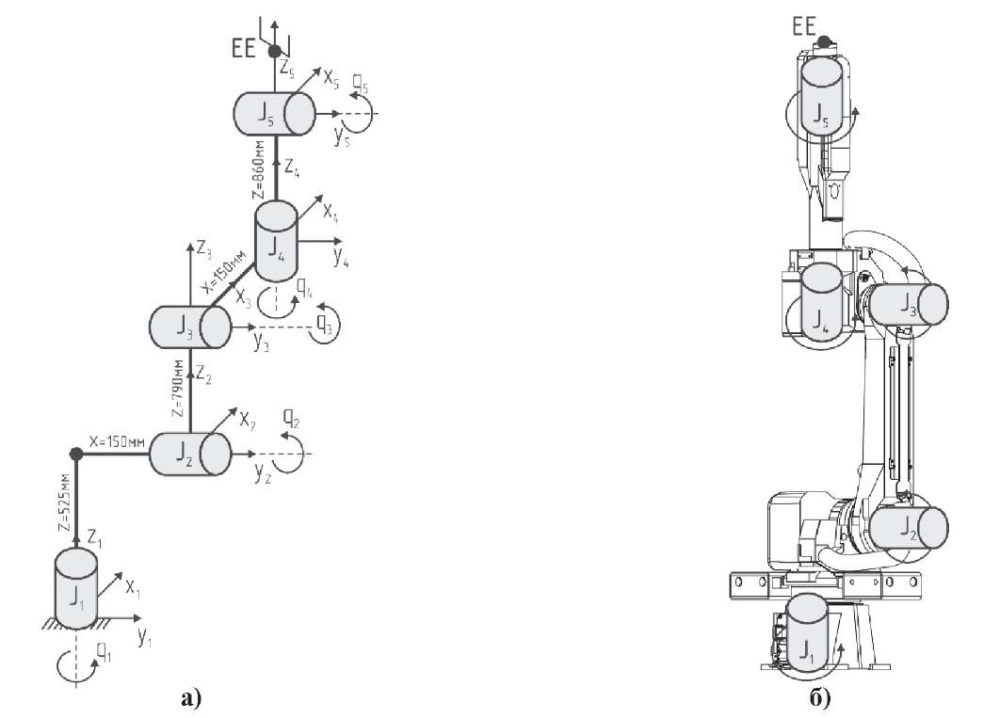
Рис. 3. Система координат манипулятора FANUC Robot M-20iA/35M
а) смещение осей вращения в сочленениях манипулятора;
б) оси вращения в соответствии с твердотельной моделью манипулятора
Примечание: составлено автором.
Решение прямой задачи кинематики заключается в расчете координат положения и ориентации системы координат, связанной с рабочим органом, при заданном наборе обобщенных координат манипулятора [7]. Для ее решения обычно используют тот или иной метод преобразования координат [8–10]. Основой расчета является построение однородной матрицы преобразования (или матрица манипулятора) T размерностью 4×4, описывающей положение системы координат каждого звена манипулятора относительно системы координат предыдущего. Матрицу T можно представить как блочную матрицу вида:
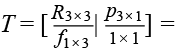
 (1)
(1)
где R3×3 – матрица поворота размерностью 3×3;
p3×1 – матрица 3×1, задающая положение вектора начала повернутой системы координат отдельного звена относительно абсолютной;
f1×3 – матрица размерностью 1×3, задающая преобразование перспективы;
1×1 – глобальный масштабирующий множитель (глобальное сжатие или расширение координат).
Система координат OXYZ фиксирована в трехмерном пространстве и принята за абсолютную. В качестве абсолютной системы выступает центр неподвижного основания робота. Система координат, которая вращается относительно абсолютной и физически рассматривается как связанная система координат, обозначается OUVW. Система OUVW жестко связана с твердым телом (сочленениями манипулятора) и движется вместе с ним. Подматрица p3×1 – однородная матрица преобразования – задает параллельный перенос системы координат OUVW относительно абсолютной системы OXYZ на вектор p̂ = (px , py , pz , 1)T. Глобальный масштабирующий множитель для роботов-манипуляторов принимается равным единице [4]. Матрица f1×3, задающая преобразование перспективы, для универсального манипулятора состоит из нулевых элементов. Отличные от нуля значения матрицы f1×3 используются в задачах машинного зрения. Матрицу поворота R3×3 можно определить как матрицу преобразования трехмерного вектора положения в евклидовом пространстве, переводящую его из повернутой (связанной со манипулятора) системы отсчета OUVW в абсолютную, неподвижную, систему координат OXYZ. Матрицы элементарных поворотов по осям координат Rx, α, Ry, φ и Rz, θ имеют следующий вид:
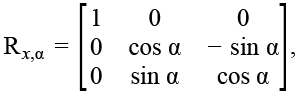
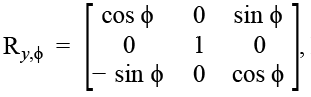
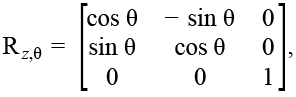 (2)
(2)
где x, y, z – оси, вокруг которых осуществляется поворот;
α, φ, θ – углы поворота.
Однородная матрица композиции преобразований манипулятора (1) может быть получена путем перемножения однородных матриц элементарных поворотов и сдвигов для каждого звена:
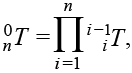 (3)
(3)
где n – число подвижных звеньев;
i – номер звена.
Для кинематической схемы манипулятора FANUC Robot M-20iA/35M (см. рис. 2а) число подвижных звеньев n = 6, все сочленения вращательного типа. Сдвиг по осям координат каждого последующего звена относительно предыдущего показан на схеме в направлениях соответствующих осей. Решение прямой задачи кинематики для шестизвенного манипулятора является вопросом вычисления матрицы с помощью последовательного перемножения шести смежных матриц . Однородные матрицы преобразований для каждого сочленения в соответствии со схемой (см. рис. 2а) будут иметь следующий вид:
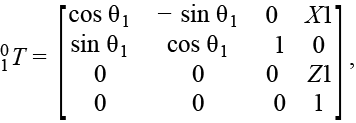
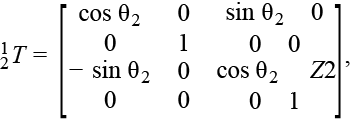
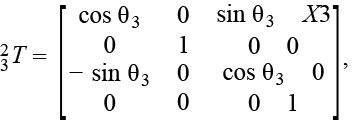
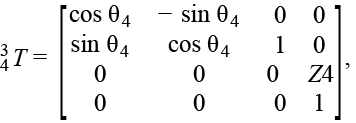

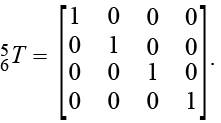
Однородная матрица преобразования для конечного эффектора манипулятора (матрица ) состоит из единичной матрицы с нулевым сдвигом по координатам [11]. Это объясняется тем, что для решения задачи, поставленной в статье, не требуется учитывать вращение шпинделя конечного эффектора. Результирующая, единственная однородная матрица решения прямой задачи кинематики манипулятора FANUC Robot M-20iA/35M:
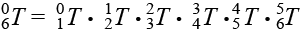 . (4)
. (4)
Аналитическое выражение матрицы манипулятора имеет достаточно громоздкий вид и в статье не приводится. Однако полученное математическое выражение (4) используется в блочной модели для проверки правильности расчетов.
Для анализа траектории движения манипулятора и проверки правильности вычисления результирующей матрицы манипулятора использовалась система SIMULINK системы MATLAB. Твердотельная модель манипулятора FANUC Robot M-20iA/35M разработана с использованием CAD-системы (SolidWorks 3D CAD Design Software). При анализе динамики движения использовался гибридный подход, заключающийся в импортировании модели манипулятора в специализированный пакет расширения SimMechanics [12]. Данный пакет служит для моделирования и расчета многодельных пространственных механизмов; в частности, SimMechanics широко используется для решения задач прямой и обратной кинематики и динамики роботов. Блок-схема импорта модели показан на рис. 4, сам механизм импорта подробно описан в [12][13]. Для импорта модели манипулятора в систему MATLAB использовалась утилита SimScape Multibody Link, которая преобразует данные механической системы из CAD-системы в приложение физического моделирования SimScape Multibody. Утилита SimScape Multibody Link генерирует два файла. Первый файл (*.stl) содержит информацию о геометрии твердотельной модели, во втором файле (*.xml) содержится информация о сопряжении деталей в CAD-сборке и их физических характеристиках (моменты инерции, масса и объем). На основе двух полученных файлов генерируется блочная Simulink-модель (файл *.slx) со связями и сопряжениями в системе SimMechanics [14].
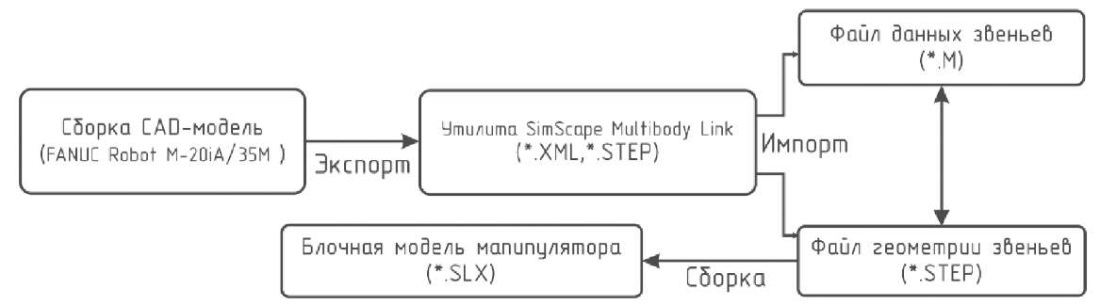
Рис. 4. Импорт CAD-модели манипулятора FANUC Robot M-20iA/35M
в систему MATLAB/Simulink
Примечание: составлено автором.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Имитационная модель манипулятора FANUC Robot M-20iA/35M, импортированная в систему Simulink/SimScape Multibody, представлена на рис. 5.
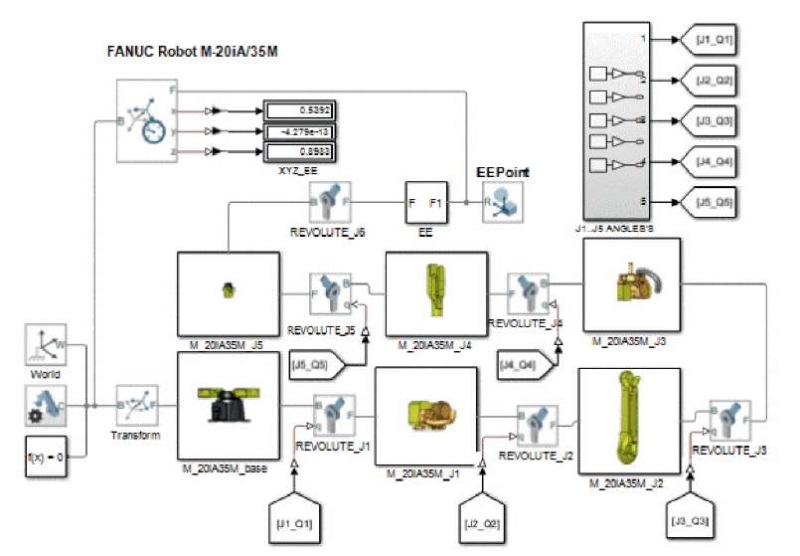
Рис. 5. Блочная Simulink/SimScape модель манипулятора FANUC Robot M-20iA/35M
Примечание: составлено автором.
Твердотельные элементы манипулятора (блоки M_20iA35M_J1…J5) в блочной модели соединяются между собой и с неподвижным основанием (блок M_20iA35M_base) при помощи сочленений (блоки REVOLUTE_J1…J5 на рис. 5). Блоки REVOLUTE_J1…J5 обеспечивают одну вращательную степень свободы. При реализации как прямой, так и инверсной кинематики сочленения манипулятора должны вращаться в некоторых пределах, ограничения вращения сочленений манипулятора определяются только физическими пределами изменения углов θi для каждого из них. Пределы изменения углов для FANUC Robot M-20iA/35M даны в таблице и задаются в модели как параметры блоков REVOLUTE_J1…J5 (параметр сonstraints-блоков). На вход блоков REVOLUTE_J1…J5 подается внешний сигнал управления, который соответствует величине угла поворота для каждого из сочленений. Данные сигналы генерирует блок J1…J5 ANGLE’S.
На рис. 6 показана твердотельная модель манипулятора FANUC Robot M-20iA/35M при симуляции перемещения его рабочего органа в окне Mechanics Explorer системы Simulink. Точка, которая соответствует положению конечного эффектора манипулятора и координаты которой отслеживаются, показана в окне Mechanics Explorer в виде маркера (на рис. 6 в системе Mechanics Explorer маркер изображен в виде сферы).
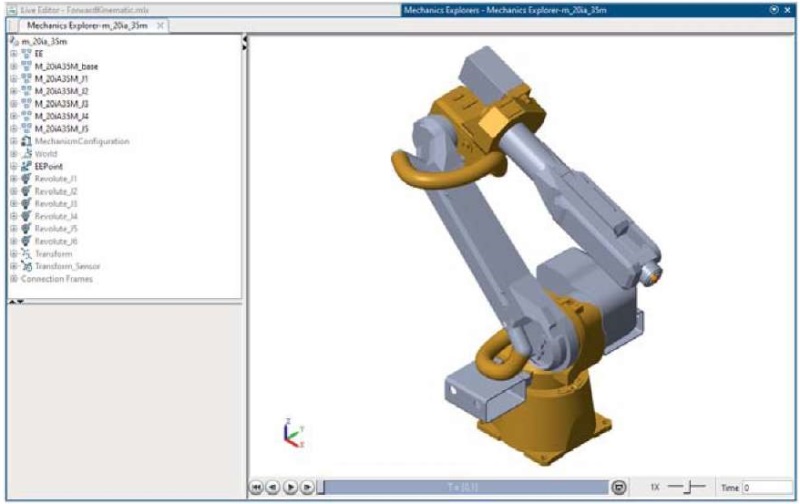
Рис. 6. Моделирование перемещения манипулятора FANUC Robot M-20iA/35M
в окне Mechanics Explorer системы Simulink
Примечание: составлено автором.
На рис. 6 показано положение конечного эффектора манипулятора для углов сочленений θ1 = 0, θ2 = 45, θ3 = 65, θ4 = 0, θ5 = 0. Шестой угол и шестая степень свободы отвечают за вращение вокруг своей оси самого конечного эффектора. В связи с тем что СТЗ крепится к конечному эффектору манипулятора, для получения изображения анализируемой поверхности детали не требуется вращение камеры вокруг своей оси, поэтому принималось, что конечный эффектор неподвижен. Это упростит аналитическое выражения матрицы манипулятора 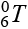 , так как матрица преобразований
, так как матрица преобразований 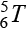 для конечного эффектора не будет содержать тригонометрических функций. В блочной модели (рис. 5) положение эффектора, его координаты относительно неподвижной системы отчета отслеживались блоком XYZ_EE. Блок выводит координаты X, Y и Z в зависимости от заданных углов сочленений. Так, для заданных углов сочленений θ1 = 0, θ2 = 45, θ3 = 65, θ4 = 0 и θ5 = 0 координаты конечного эффектора после проведения моделирования будут [ 0,5392;0;0,8984]. Решение прямой задачи с использованием матрицы манипулятора (4) в среде MATLAB дает аналогичные значения координат конечного эффектора. На рис. 7 показано аналитическое и численное решение. Красным маркером выделены значения, полученные для вышеобозначенных углов θ1… θ5.
для конечного эффектора не будет содержать тригонометрических функций. В блочной модели (рис. 5) положение эффектора, его координаты относительно неподвижной системы отчета отслеживались блоком XYZ_EE. Блок выводит координаты X, Y и Z в зависимости от заданных углов сочленений. Так, для заданных углов сочленений θ1 = 0, θ2 = 45, θ3 = 65, θ4 = 0 и θ5 = 0 координаты конечного эффектора после проведения моделирования будут [ 0,5392;0;0,8984]. Решение прямой задачи с использованием матрицы манипулятора (4) в среде MATLAB дает аналогичные значения координат конечного эффектора. На рис. 7 показано аналитическое и численное решение. Красным маркером выделены значения, полученные для вышеобозначенных углов θ1… θ5.
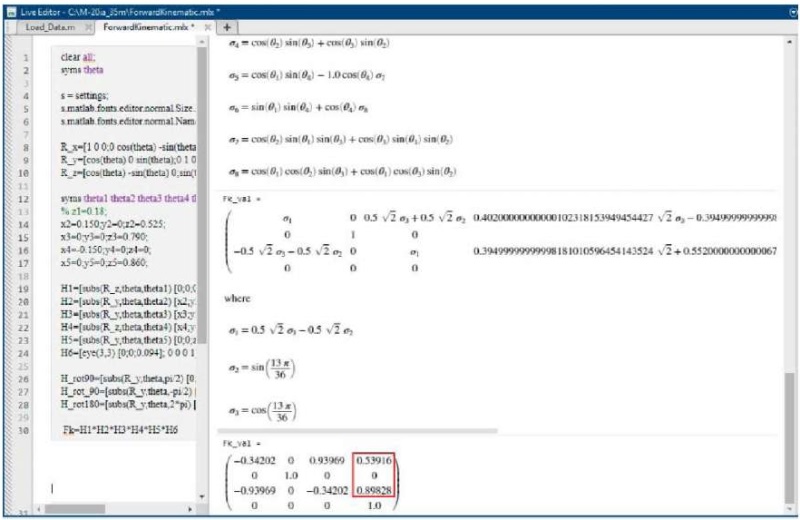
Рис. 7. Численное решение матрицы манипулятора в среде MATLAB
Примечание: составлено автором.
Для получения численного результата при задании значений углов для матрицы манипулятора использовались среда MATLAB и визуальный редактор Live Editor [15]. В окно Live Editor в виде исполняемого скрипта вносились аналитические выражения для матрицы элементарных поворотов по осям координат (выражение 2) и конечной матрицы манипулятора (выражение 4). Значение углов поворота каждого шарнира (θ1… θ5) задавались как константы. Результирующая матрица манипулятора 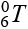 и ее аналитическое выражение вычислялись как произведение матриц отдельных звеньев. В результате работы скрипта в окне Live Editor отображается аналитическое выражение матрицы
и ее аналитическое выражение вычислялись как произведение матриц отдельных звеньев. В результате работы скрипта в окне Live Editor отображается аналитическое выражение матрицы 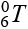 , а также значение координат X, Y, Z конечного эффектора FANUC Robot M-20iA/35M (на рис. 7 полученные координаты выделены красным).
, а также значение координат X, Y, Z конечного эффектора FANUC Robot M-20iA/35M (на рис. 7 полученные координаты выделены красным).
ЗАКЛЮЧЕНИЕ
В работе решена прямая кинематическая задача с применением гибридного подхода моделирования манипулятора FANUC Robot M-20iA/35M с шестью степенями свободы. Полученное аналитическое решение матрицы манипулятора 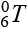 позволяет для каждого момента времени определить положение его исполнительного органа. В дальнейшем предложенная блочная Simulink-модель может быть дополнена и усовершенствована для учета ориентации конечного эффектора манипулятора при решении задачи инверсной кинематики.
позволяет для каждого момента времени определить положение его исполнительного органа. В дальнейшем предложенная блочная Simulink-модель может быть дополнена и усовершенствована для учета ориентации конечного эффектора манипулятора при решении задачи инверсной кинематики.
Список литературы
1. FANUC global. URL: https://www.fanuc.com/ (дата обращения: 15.04.2024).
2. Лесков А. Г., Морошкин С. Д. Система технического зрения для определения расположения объектов // Экстремальная робототехника : тр. междунар. науч.-технич. конф., 24‒25 ноября 2016 г., г. Санкт-Петербург. СПб. : ООО «АП4Принт», 2016. С. 287‒290.
3. Angeles J. Fundamentals of robotic mechanical systems. Theory, methods and algorithms. 4th ed. Switzerland : Springer, 2014. 589 p.
4. Фу К., Гонсалес Р., Ли. К. Робототехника. М. : Мир, 1989. 624 с.
5. Колтыгин Д. С., Седельников И. А. Метод и программа решения прямой и обратной задачи кинематики для управления роботом-манипулятором // Системы. Методы. Технологии. 2020. № 4. C. 65–74. DOI 10.18324/2077-5415-2020-4-65-74.
6. Садков К. О., Моногаров С. И. Роботизированный манипулятор с шестью степенями свободы // Наука, техника и образование. 2018. № 8. C. 37–43.
7. Karger A. Singularity analysis of serial robot-manipulators // Journal of Mechanical Design. 1996. Vol. 118, no. 4. P. 520‒525.
8. Denavit J., Hartenberg R. S. A kinematic notation for lower-pair mechanisms based on matrices // Journal of Applied Mechanics. 1955. Vol. 22, no. 2. P. 215‒221.
9. Hayati S., Mirmirani M. Improving the absolute positioning accuracy of robot manipulators // Journal of Robotic Systems. 1985. Vol. 2, no. 4. P. 397‒413.
10. Brandstötter M., Angerer A., Hofbaur M. An analytical solution of the inverse kinematics problem of industrial serial manipulators with an ortho-parallel basis and a spherical wrist. // Proceedings of the Austrian Robotics Workshop, May 22‒23, 2014, Linz, Australia. Vol. 22. 2014. P. 7‒11.
11. Singla A., Singh G., Virk G. S. Matlab/simMechanics based control of four-bar passive lower-body mechanism for rehabilitation // Perspectives in Sciences. 2016. Vol. 8. P. 351‒354.
12. Hroncova D., Pastor M. Mechanical system and Sim-Mechanics simulation // American Journal of Mechanical Engineering. 2013. Vol. 1, n o. 7. P. 251‒255.
13. Achilli G. M., Logozzo S., Valigi M. C. et al. Underactuated soft gripper for helping humans in harmful works // Proceedings of I4SDG Workshop 2021 / Quaglia G., Gasparetto A., Petunya V., Carbone G., eds. Cham : Springer, 2021. P. 264‒272.
14. Гусев О. В. Имитационное моделирование захвата антропоморфной кисти руки // Вестник кибернетики. 2023. Т. 22, № 4. C. 18–25.
15. MATLAB live editor. URL: https://nl.mathworks. com/products/matlab/live-editor.html (дата обращения: 15.04.2024).
Об авторе
Олег Валерьевич ГусевРоссия
кандидат физико-математических наук, доцент
Рецензия
Для цитирования:
Гусев О.В. РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ КИНЕМАТИКИ ДЛЯ ШЕСТИЗВЕННОГО РОБОТА-МАНИПУЛЯТОРА. Вестник кибернетики. 2024;23(2):39-48. https://doi.org/10.35266/1999-7604-2024-2-5
For citation:
Gusev O.V. SOLVING THE DIRECT KINEMATIC PROBLEM FOR A SIX-UNIT ROBOT MANIPULATOR. Proceedings in Cybernetics. 2024;23(2):39-48. (In Russ.) https://doi.org/10.35266/1999-7604-2024-2-5















