Перейти к:
Метод визуально управляемого захвата 7-степенного манипулятора на основе обучения с подкреплением
https://doi.org/10.35266/1999-7604-2025-1-5
Аннотация
В данной статье описывается решение задачи обратной кинематики для захвата объектов с помощью 7-степенного манипулятора Franka Emika Panda, основанное на использовании компьютерного зрения. В предложенном нами решении, работа в режиме физической симуляции основывается на алгоритме обучения с подкреплением из области машинного обучения и дополняется алгоритмом компьютерного зрения для определения геометрической структуры объекта и проведения обучения, что обеспечивает реализацию всего алгоритмического процесса. Процесс решения задачи, создание соответствующей среды и результаты комбинированного алгоритма с использованием нейронных сетей демонстрируют его эффективность в решении сложных задач обратной кинематики. Это низкозатратная современная технология, которая может быть широко применена для выполнения аналогичных задач с другими типами манипуляторов.
Ключевые слова
Для цитирования:
Цао И. Метод визуально управляемого захвата 7-степенного манипулятора на основе обучения с подкреплением. Вестник кибернетики. 2025;24(1):31-38. https://doi.org/10.35266/1999-7604-2025-1-5
For citation:
Cao Y. Vision-based grasping method for 7-DOF manipulator using reinforcement learning. Proceedings in Cybernetics. 2025;24(1):31-38. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-5
ВВЕДЕНИЕ
Роботизированные манипуляторы широко используются в современной промышленности и оказывают значительное влияние на процессы индустриального производства. Классические методы управления такими манипуляторами можно разделить на три основные категории.
- Ручное управление с использованием пульта оператора.
Преимущество этого метода заключается в том, что человек-оператор может гибко избегать препятствий и справляться с внезапными ситуациями. Недостатком является значительное потребление времени оператора.
- Метод обучения через демонстрацию.
В этом подходе манипулятор управляется вручную для записи траектории, которая затем воспроизводится. Преимущество заключается в экономии времени, но в случае изменения положения целевого объекта требуется повторная запись траектории.
- Автоматизация через предварительное программирование.
Этот метод заключается в том, что инженер заранее разрабатывает программу для автоматического управления манипулятором. Планирование траектории осуществляется с использованием теорий прямой кинематики (вычисление положения концевого эффектора на основе геометрии и углов вращения суставов) и обратной кинематики (вычисление углов вращения суставов на основе заданного положения концевого эффектора). Обратная кинематика [1] позволяет сэкономить время оператора и хорошо подходит для задач захвата объекта, однако она сложнее, чем прямая кинематика из-за наличия множественных решений и проблемы выбора оптимального решения. Кроме того, ее гибкость ограничена при наличии препятствий.
Для реализации более гибкого автоматического планирования траекторий манипулятора в данной работе предложено использование физического 3D-симулятора PyBullet [2]. В симуляции применяется открытая модель манипулятора Franka Emika Panda, что позволяет безопасно проводить эксперименты в виртуальной среде без физического риска, основанной на данных из множества симулированных сред и накопленного опыта взаимодействия с помощью обучения с подкреплением.
Обучение с подкреплением представляет собой важное направление в области искусственного интеллекта (ИИ) и машинного обучения (МО). Этот подход позволяет обучаться на основе взаимодействий с окружающей средой, изучая закономерности и разрабатывая стратегии поведения. Большое количество исследований посвящено применению обучения с подкреплением в таких областях, как классические игры (например, покер, го) [3] и видеоигры [4]. В данной работе предлагается использование физического симулятора для создания модели манипулятора и построения соответствующей среды. Алгоритмы обучения с подкреплением интегрируются в эту среду, а данные, полученные в симуляции, используются для тренировки нейронной сети, способной автоматически управлять манипулятором. В результате достигается интеллектуальное планирование траекторий для манипулятора.
МАТЕРИАЛЫ И МЕТОДЫ
О. В. Гусев в [5] описал последовательность решения прямой задачи кинематики через вычисление углов поворота сочленений, то есть определение конечного положения захвата манипулятора на основе заданных углов вращения его сочленений численными методами. Для задачи захвата объекта процесс обратный – решение задачи обратной кинематики, для которой существует множество решений. Однако некоторые из них могут приводить к столкновениям, и такие решения необходимо исключать. Поскольку это не всегда очевидно, некоторые исследователи предложили использовать обучение с подкреплением в компьютерной симуляционной среде для выполнения задачи захвата объектов без столкновений. Например, Li и соавт. [6] реализовали обучение с подкреплением в Unity для моделирования захвата объекта снизу-вверх. Malik и соавт. [7] исследовали применение обучения с подкреплением для достижения манипулятором нескольких целевых точек во время движения. Кальдерон и соавт. в [8] изучили методику использования RGB-D камеры, установленной на захвате, чтобы приблизиться к определенному объекту.
Мы предлагаем метод, использующий фиксированную RGB-D камеру с фиксированным углом обзора. На начальном этапе камера определяет положение объекта с помощью анализа RGB-D данных, а затем манипулятор выполняет захват объекта в трехмерном пространстве. Такая траектория захвата объекта сверху вниз выглядит более естественной. Кроме того, в отличие от метода, предложенного Кальдероном и соавт. [8], наш подход не требует постоянного анализа данных с RGB-D камеры в режиме реального времени, что снижает вычислительную нагрузку на аппаратное обеспечение.
Робот-манипулятор Franka Emika Panda оснащен 7 шарнирами, обладает грузоподъемностью до 3 кг, весит около 18 кг и имеет точность повторного позиционирования 0,1 мм [9]. Его модель в физическом симуляторе PyBullet на рис. 1.
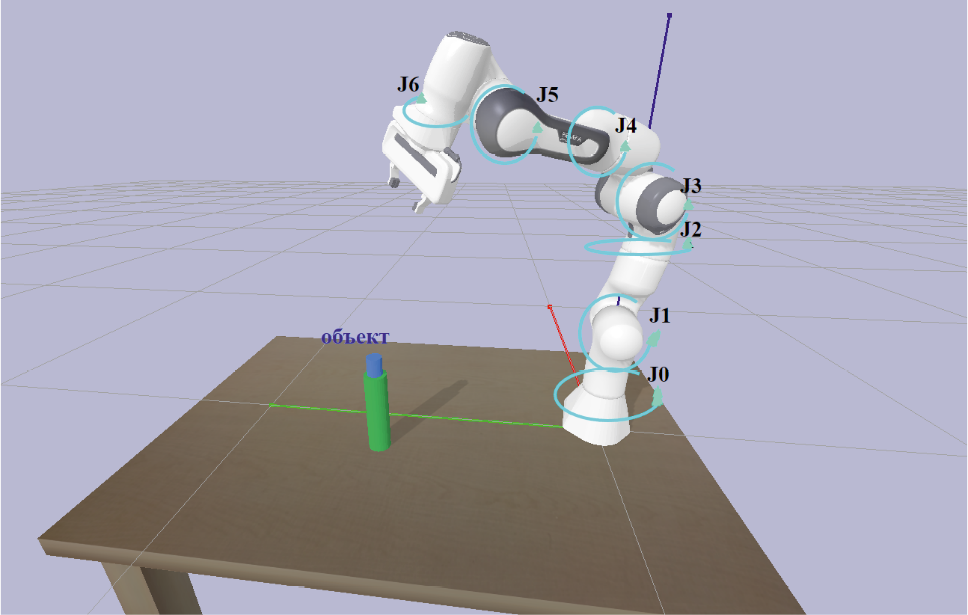
Рис. 1. Задачи компьютерного моделирования в PyBullet
Примечание: изображение получено автором.
Соответствующие ему шарнирные соединения обозначены на рис. 1 как J0 …J6.
Решаемая задача может быть сформулирована следующим образом:
Известно, что база манипулятора расположена в точке (0,0,0), начальные углы шарниров заданы как [θ0… θ6]. Также известны положение и параметры камеры, а положение целевого объекта определяется на основе данных RGB-D изображения, полученного с камеры. Требуется найти траекторию движения манипулятора для захвата целевого объекта. Схема моделирования данной задачи представлена на рис. 1 (синий – объект, зеленый – поддержка).
Для решения задачи предлагается следующий подход:
- Вычислить реальные координаты целевого объекта в системе координат манипулятора на основе их положения в системе координат RGB-D камеры.
- Разработать обучающую среду для алгоритма обучения с подкреплением по данным п. 1.
Преобразование координат из системы камеры в реальный мир
RGB-D камера позволяет получить изображения с данными о глубине. После сегментации с использованием сегментационной нейронной сети можно получить пиксельные координаты (u, v, zc), где u и v – координаты пикселя, а zc – глубина.
Процесс вычисления координат в реальном мире описывается следующими матричными операциями (1):
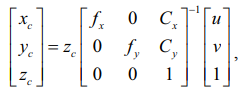 (1)
(1)
где:

fov – угол обзора камеры, соотношение сторон (aspect) и разрешение изображения (width, height);
(xc, yc, zc) – положение объекта в системе координат камеры;
fx, fy – фокусное расстояние камеры;
Cx, Cy – положение оптического центра камеры.
Относительно мировых координат, где робот-манипулятор является точкой отсчета (2):
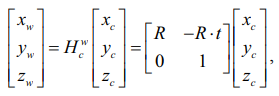 (2)
(2)
где:
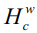 представляет матрицу преобразования объекта из камеры в мировую систему координат;
представляет матрицу преобразования объекта из камеры в мировую систему координат;
(xw, yw, zw) – положение объекта в системе координат мира;
R – матрица поворота (3):
 (3)
(3)
где:
focus_pos, camera_pos – координаты фокуса камеры и координаты камеры;
вектор 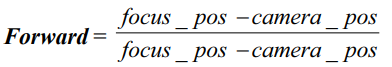
– направление камеры на фокусе;
вектор 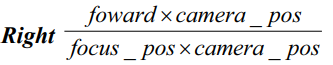
– правое направление камеры;
вектор Up = right × forward – верхнее направление камеры;
t – вектор переноса.
Таким образом, мы можем получить координаты объекта относительно в мировую систему координат из изображения с камеры RGB-D.
Создание среды обучения с подкреплением
Глубокое обучение с подкреплением представляет собой класс алгоритмов end-to-end обучения. К наиболее распространенным алгоритмам глубокого обучения с подкреплением относятся DDPG (Deep Deterministic Policy Gradient) [10], SAC (Soft Actor-Critic) [11] и PPO (Proximal Policy Optimization – оптимизация проксимальной политики) [12]. Процесс глубокого обучения с подкреплением состоит из следующих пяти основных компонентов, как описано в используемой среде Gymnasium:
- Агент (Agent): сущность, принимающая решения (в данном случае – манипулятор), которая обучается, взаимодействуя с заданной средой.
- Среда (Environment): описание задачи и окружения, в котором действует агент.
- Действие (Action): действия, предпринимаемые агентом.
- Состояние (State): основа, на которой агент принимает решение о выполнении действий.
- Вознаграждение (Reward): оценка действий агента в среде, которая используется для определения последующих действий.
В данной работе используется алгоритм PPO. Схема его работы представлена на рис. 2.
PPO основан на архитектуре сети актор-критик (Actor-Critic), что позволяет эффективно решать задачи в пространстве непрерывных действий. Актор-сеть: на вход получает состояние среды s, а на выходе формирует действие a и вероятность, связанную с этим действием. Критик-сеть: на вход получает состояние s и на выходе оценивает значение v, которое отражает изменения состояния среды после выполнения действия a. Она также рассчитывает преимущество и связанную с ним потерю стоимости TD-ошибка (Temporal difference Error). Убыток используется для обновления параметров критик-сети. Преимущество комбинируется с параметрами вероятности из актор-сети, чтобы вычислить совокупный убыток Lclip (θ) для актор-критика сети, который затем используется для обновления ее параметров. Подробный процесс расчета можно найти в оригинальной статье [8].
Процесс создания среды обучения с подкреплением для манипулятора заключается в следующем:
Шаг 1. Инициализация среды и задание начальных углов для всех суставов манипулятора. Целевой объект размещается в случайных позициях в пределах заданного диапазона.
Шаг 2. Агент предпринимает действия на основе текущего состояния среды, а также распознанного положения объекта.
Шаг 3. Агент рассчитывает награждение на основе предпринятых действий и обратной связи от среды.
Шаг 4. Шаги 2 и 3 повторяются до достижения условия завершения (успешное выполнение задачи или неудача).
Шаг 5. Переход к шагу 1.
Процесс проиллюстрирован на рис. 3.
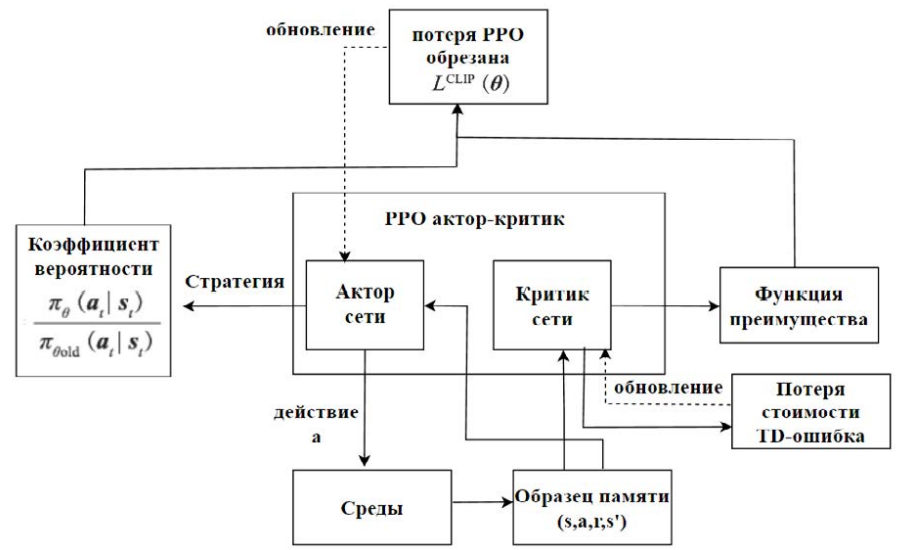
Рис. 2. Архитектура алгоритма PPO
Примечание: изображение получено автором.
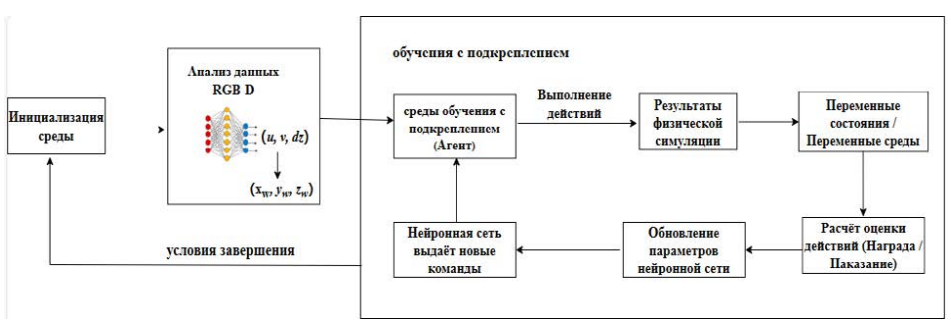
Рис. 3. Схема работы системы управления манипулятора
Примечание: составлено автором.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В процессе обучения с использованием метода глубокого обучения с подкреплением был применен алгоритм PPO в симуляции PyBullet. Обучение проводилось на ноутбуке с процессором Intel i7–11800H @ 2,3 ГГц в режиме CPU с 16 потоками одновременно на Python 3.11. Для успешного выполнения задачи считалось, что центр захвата конечного эффектора находится на расстоянии не более 2 см прямо над объектом. Общая продолжительность обучения составила 20 миллионов временных шагов за 2 часа 45 минут. Результаты процесса обучения задачи были записаны в TensorBoard.
На рис. 4 по оси X отображены временные шаги задачи, по оси Y (eval/success_rate) показан общий уровень успешности сети на соответствующем этапе. Из графика видно: на интервале 0–10 миллионов временных шагов успешность модели значительно колебалась. На интервале 10–14 миллионов шагов модель часто достигала 100 % успешности. На интервале 14–17 миллионов шагов успешность практически стабилизировалась на уровне 100 %, что свидетельствует о нахождении оптимальной стратегии. В оставшиеся шаги (до 20 миллионов) успешность оставалась низкой и практически не менялась.
Для валидации был проведен случайный тест с использованием обученной оптимальной модели. Часть результатов приведена на рис. 5.
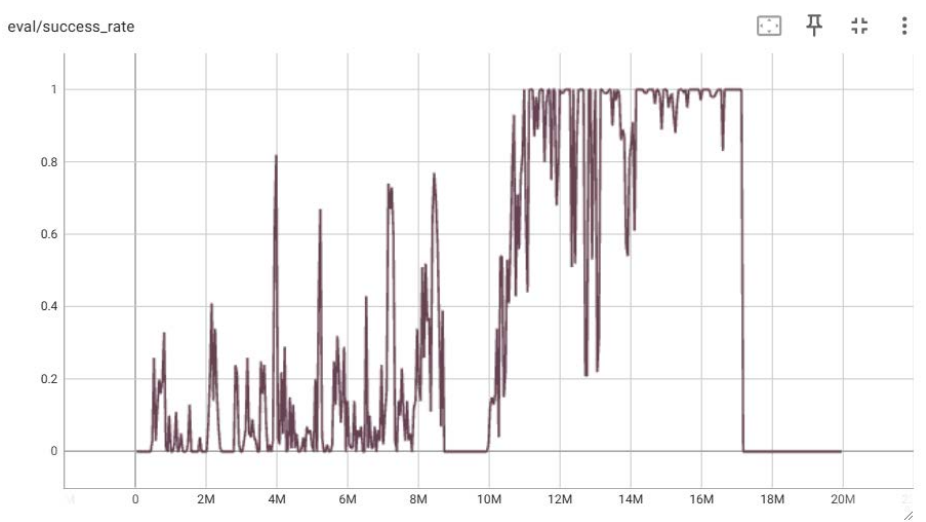
Рис. 4. Схема работы системы управления манипулятора
Примечание: составлено автором.
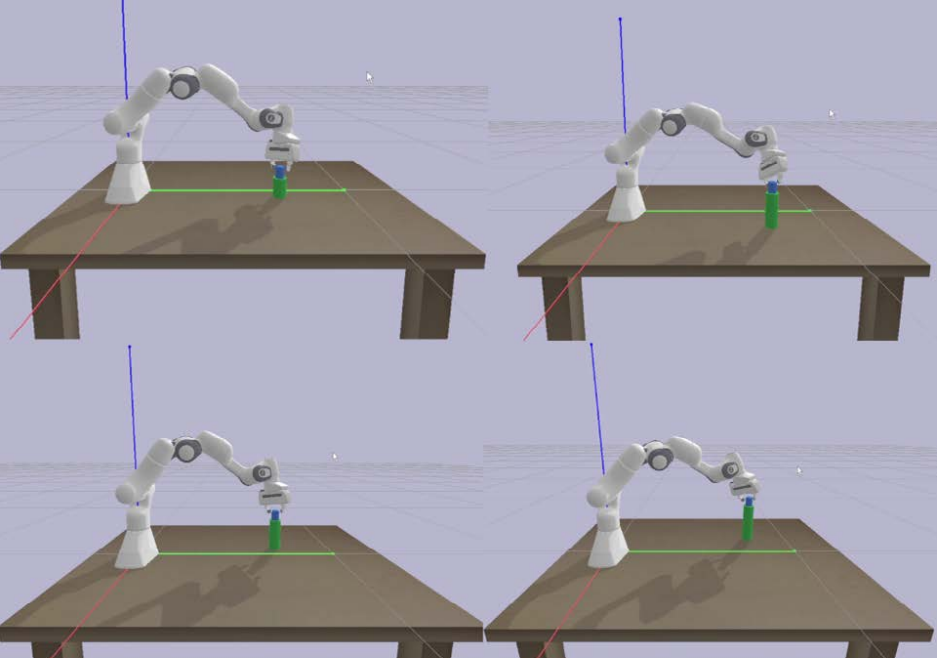
Рис. 5. Случайное тестирование для проверки нейронных сетей
Примечание: составлено автором.
ЗАКЛЮЧЕНИЕ
В данной работе использовано программное обеспечение для физической симуляции PyBullet для моделирования робот-манипулятора. В среде Gymnasium была абстрактно описана задача, а для обучения использован алгоритм обучения с PPO, который позволил решить задачу обратной кинематики, связанную с захватом объекта на основе визуального руководства.
Предложенный нами метод после обучения продемонстрировал 100-процентную успешность нейронной сети в тысяче случайных тестов. Время вывода для одного шага составляет 2 мс, а общее время вывода для всего процесса захвата составляет около 160–180 мс. Для сравнения, типичный алгоритм решения обратной кинематики в PyBullet, DLS (Damped Least Squares), работает быстрее – около 12 мс. Однако использование алгоритма обучения с подкреплением обеспечивает более плавную траекторию движения манипулятора, что делает его наиболее подходящим для решения сложных и динамичных задач. В будущем планируется усовершенствовать модель алгоритма для решения задач, связанных с захватом движущихся объектов и среды с препятствиями.
Список литературы
1. He Y., Liu S. Analytical inverse kinematics for Franka Emika Panda – A geometrical solver for 7-DOF manipulators with unconventional design // Proceedings of 9th International Conference on Control, Mechatronics and Automation (ICCMA), 2021. IEEE, 2021. p. 194–199.
2. Bullet Real-Time Physics Simulation. URL: https://pybullet.org/wordpress/ (дата обращения: 14.01.2025).
3. Silver D., Hubert T., Schrittwieser J. et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play // Science. 2018. Vol. 362, no. 6419. P. 1140–1144.
4. Torrado R. R., Bontrager P., Togelius J. et al. Deep reinforcement learning for general video game AI // Proceedings of IEEE Conference on Computational Intelligence and Games (CIG), 2018. IEEE, 2018. P. 1–8.
5. Гусев О. В. Решение прямой задачи кинематики для шестизвенного робота-манипулятора // Вестник кибернетики. 2024. Т. 23, № 2. С. 39–48.
6. Li H., Zhao Zh., Lei G. et al. Robot arm control method based on deep reinforcement learning // Journal of System Simulation. 2019. Vol. 31, no. 11. P. 2452–2457.
7. Malik A., Lischuk Y., Henderson T. et al. A deep reinforcement-learning approach for inverse kinematics solution of a high degree of freedom robotic manipulator // Robotics. 2022. Vol. 11, no. 2. P. 44–61.
8. Calderón-Cordova C., Sarango R., Castillo D. et al. A deep reinforcement learning framework for control of robotic manipulators in simulated environments // IEEE Access. 2024. Vol. 12. P. 103133–103161.
9. Franka Emika Panda. URL: https://robodk.com.cn/robot/ru/Franka/Emika-Panda (дата обращения: 14.01.2024).
10. Lillicrap T. P., Hunt J. J., Pritzel A. et al. Continuous control with deep reinforcement learning // arXiv preprint arXiv:1509.02971. 2015.
11. Fujimoto S., Hoof H., Meger D. Addressing function approximation error in actor-critic methods // Proceedings of the 35th International conference on machine learning, 2018, Stockholm. PMLR, 2018. p. 1587–1596.
12. Schulman J., Wolski F., Dhariwal P. et al. Proximal policy optimization algorithms // arXiv preprintarXiv:1707.06347. 2017.
Об авторе
И. ЦаоРоссия
аспирант
Рецензия
Для цитирования:
Цао И. Метод визуально управляемого захвата 7-степенного манипулятора на основе обучения с подкреплением. Вестник кибернетики. 2025;24(1):31-38. https://doi.org/10.35266/1999-7604-2025-1-5
For citation:
Cao Y. Vision-based grasping method for 7-DOF manipulator using reinforcement learning. Proceedings in Cybernetics. 2025;24(1):31-38. (In Russ.) https://doi.org/10.35266/1999-7604-2025-1-5















